Как решать задачи на движение

Общий алгоритм решения задач на движение

Формулы

Какая бы задача на движение ни была, в ней всегда идёт речь о взаимосвязи трёх величин: расстояния S, скорости v и времени t.

Ключевая формула: S = vt.

Из неё можно выразить:

645K

Время, скорость, расстояниеЧитать →

На что ещё важно обратить внимание?

1. Среднюю скорость мы рассчитываем по формуле . Считать через среднее арифметическое будет ошибкой!

2. Скорость сближения и отдаления зависит от того, в каких направлениях двигаются объекты:

   

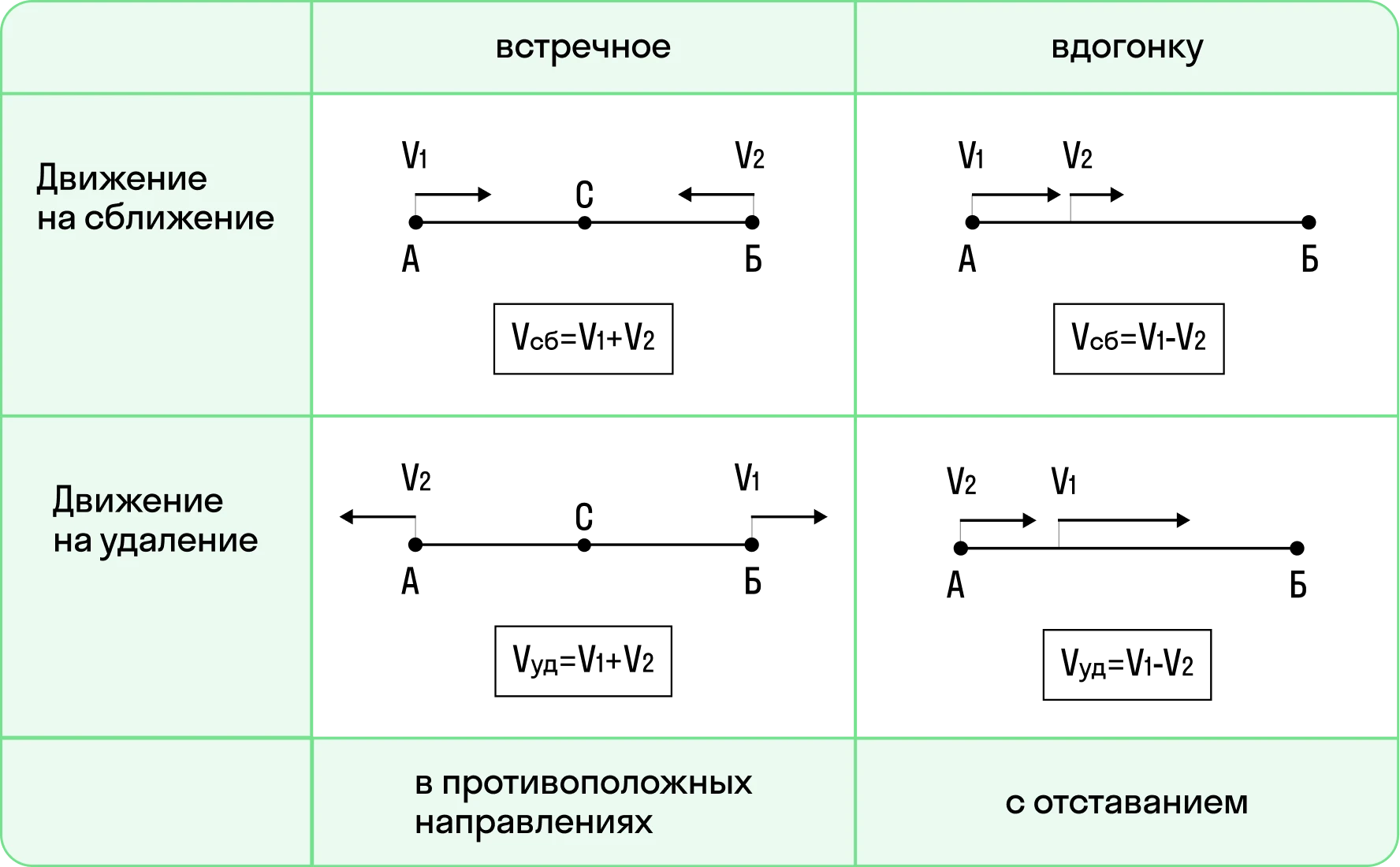
3. Для решения задачи необходимо привести все единицы измерения в одну размерность: например, мы не можем складывать км/ч и м/с.

   

   5.1K

   Единицы измерения величинЧитать →

4. Удобнее всего задачи на движение решать с помощью таблицы и схематичного рисунка.

Алгоритм

1. Анализируем текст задачи: какие данные известны, что нужно найти.
   Если необходимо, иллюстрируем задачу с помощью рисунка.

2. Заполняем таблицу исходными данными.

3. Решаем, что будем брать за x, выражаем через него величины.

4. Обращаем внимание, все ли исходные данные мы использовали.
   Часто неучтённую информацию можно использовать для обоснования уравнения.

5. Составляем уравнения или систему уравнений, решаем согласно виду.

6. Проверяем, соответствует ли ответ условию задачи и решает ли он поставленный вопрос. Если нет, вычисляем окончательный ответ.

7. Делаем проверку.

Движение по прямой: особенности решения, пример задачи с решением

Задачи на движение по прямой — самые простые по сравнению с другими видами. Чаще всего в них идёт речь о двух объектах, которые движутся навстречу друг другу или отдаляются друг от друга, скорость объектов постоянная (без ускорения), движение происходит по прямой линии.

Задача 1

Автомобиль и мотоциклист одновременно выехали навстречу друг другу из двух городов, расстояние между которыми 200 км. Скорость автомобиля — 60 км/ч, а мотоциклиста — 40 км/ч. Через сколько времени они встретятся?

Решение:

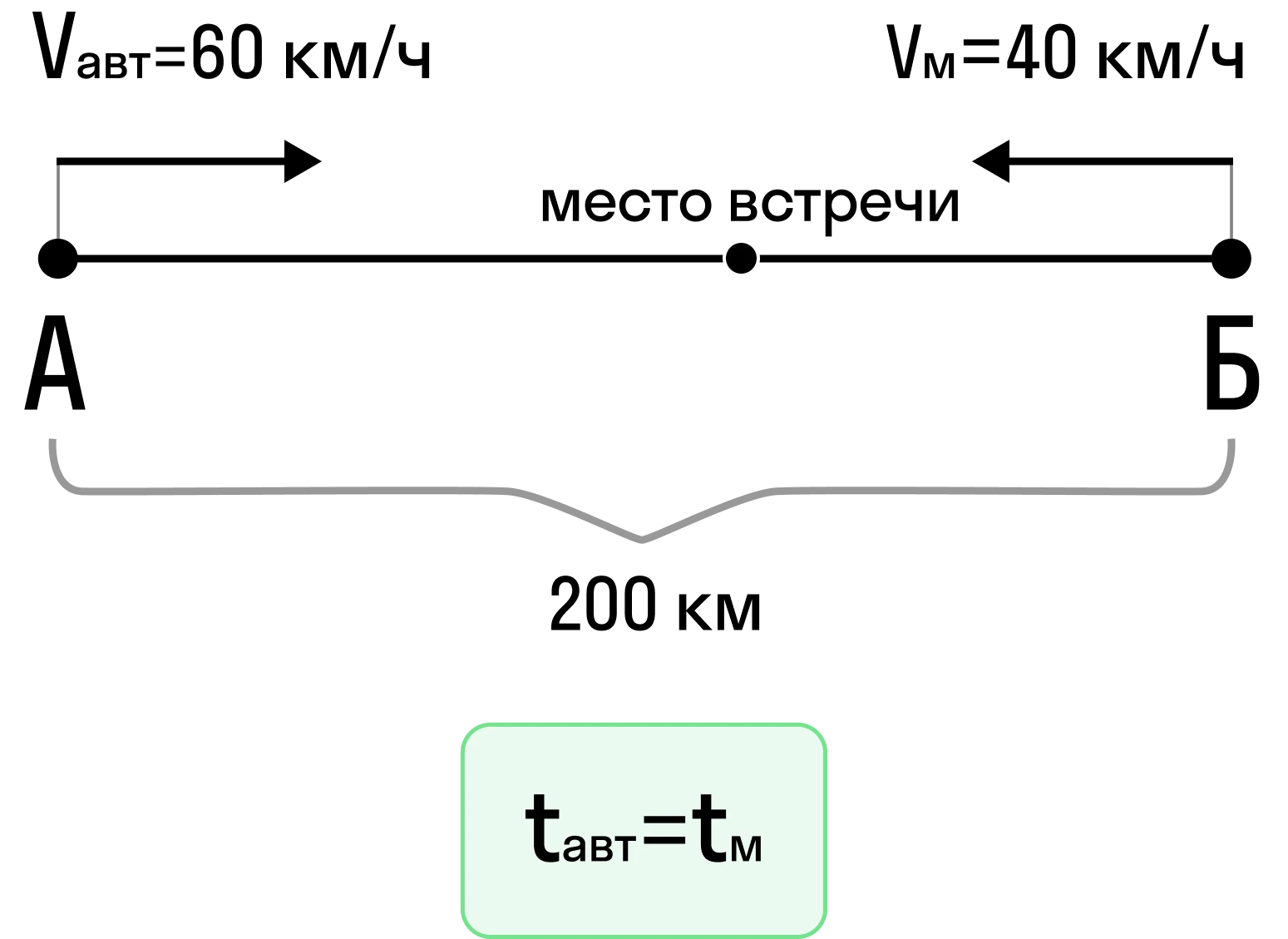
Составим таблицу по данным задачи.

	v, км/ч	t, ч	S, км
Автомобилист	60	tавт = tм	?	Вместе — 200 км
Мотоциклист	40		?

При взгляде на таблицу кажется, что неизвестного больше, чем известного. Но даже по ней и схематичному чертежу мы можем сделать следующие выводы:

1. Мы не знаем, сколько километров проедут автомобилист и мотоциклист до точки встречи, но они точно проедут 200 км совместно.

2. Так как персонажи выехали одновременно и встретят друг друга в единый момент времени .

В этой задаче можно по-разному составить уравнение.

Первый способ	Второй способ
Пусть x — время, которое затратили автомобилист и мотоциклист, тогда: 60x — расстояние автомобилиста, 40x — расстояние мотоциклиста. Так как совместно они проехали 200 км: 60x + 40x = 200 100x = 200 x = 2 (ч) — время в пути.	Пусть x — расстояние, пройденное автомобилистом, тогда: — расстояние мотоциклиста, — время автомобилиста, — время мотоциклиста. Так как время, затраченное персонажами, одинаково: (км) проехал автомобилист, тогда (ч) — время в пути.

Ответ: 2 часа.

Каким бы способом вы ни воспользовались, всё равно придёте к верному ответу!

170K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Движение по воде: особенности решения, пример задачи с решением

В задачах на движение по воде учитывается влияние на скорость плавательного средства течения реки. Если лодка или корабль плывёт по течению, река помогает двигаться быстрее, если объект плывёт против течения — река замедляет движение.

V_{по течению} = V_собств + V_реки

V_{против течения} = V_собств − V_реки

Чтобы запомнить, как вычитаются скорости при движении против течения, держите в голове мысль: река замедляет лодку, а не наоборот, поэтому скорость против течения должна быть меньше собственной скорости.

Важно: у плота нет собственной скорости, и в стоячей воде (в озере) нет течения.

Задача 2

Привычный маршрут торгового катера — выехать со своей пристани, проплыть 77 км до соседней пристани против течения реки и вернуться обратно. Обратный путь занимает на 4 ч меньше. Чему равна скорость течения, если собственная скорость катера составляет 9 км/ч?

Решение

Составим таблицу по данным задачи.

	v, км/ч	t, ч	S, км
По течению	?	? на 4 ч меньше	77
Против течения	?	?	77

При заполнении таблицы мы не использовали информацию о собственной скорости катера. Куда её записать?

Пусть x — скорость течения реки, тогда 9 + x — скорость катера по течению, 9 − x — скорость катера против течения.

Тогда — время по течению реки, — время против течения реки.

	v, км/ч	t, ч	S, км
По течению	9 + x	на 4 ч меньше tпротив теч	77
Против течения		779-x	77

Приняв во внимание разницу во времени, составим уравнение:

ОДЗ:

— не соответствует условию задачи.

Ответ: скорость течения равна 2 км/ч.

Движение по окружности: особенности решения, пример задачи с решением

Что нужно учитывать при решении задач на движение по окружности:

1. Чаще всего в таких задачах один объект будет обгонять другого на какое-то расстояние (чаще всего на круг).

2. Если тела движутся по окружности в разных направлениях, то они стремятся встретиться → цель общая, значит, их общая скорость находится как сумма скоростей каждого из них.

3. Если движение идет в одном направлении, объекты преследуют разные цели: один объект хочет догнать, а второй убежать → общая скорость будет равна разности скоростей (из большей отнимаем меньшую), при этом:

   • если скорость догоняющего больше скорости догоняемого, объекты сближаются;

   • если скорость догоняющего меньше скорости догоняемого, объекты отдаляются друг от друга.

4. При прохождении длины окружности объект возвращается в точку старта.

5. Длина окружности рассчитывается по формуле C = 2πR, где R — радиус окружности.

Задача 3

На круговой трассе длиной 16 км из одной точки одновременно стартовали два автомобиля, двигаясь в одном направлении. Первый автомобиль двигался со скоростью 120 км/ч. Через 15 минут он опередил второй автомобиль на один круг. Определите скорость второго автомобиля. Ответ укажите в км/ч.

Решение:

Проанализируем задачу:

1. За 15 минут первый автомобиль обогнал второй автомобиль на круг, то есть на 16 км.

2. Тогда за 1 час первый проедет на 4 ⋅ 16 = 64 км больше второго.

3. Это означает, что скорость второго автомобиля на 64 км/ч меньше скорости первого, т. е. 120 − 64 = 56 км/ч.

Ответ: 56 км/ч.

Задача 4

Артём и Никита договорились бегать по утрам вокруг парка. Начали движение они со входа в парк. Через 1 час, когда Артёму оставалось 2 км до завершения первого круга, он понял, что Никита пробежал первый круг 4 минуты назад.

Найдите скорость с которой бежал Никита, если известно, что она на 3 км/ч больше скорости Артёма. Ответ дайте в км/ч.

Решение:

Составим таблицу:

1. Из текста задачи следует, что Никита пробежал целый круг, а Артём — только его часть.

2. Никита пробегает круг за 1 час − 4 минуты = 56 минуты.

   56 минут = часа

Пусть x — скорость Никиты, тогда расстояние, которое он пробежал (полный круг) .

Тогда скорость Артёма (на 3 км/ч меньше, чем у Никиты) — (x − 3), и его расстояние — (x - 3) 1 = x − 3.

	v, км/ч	t, ч	S
Артём	x − 3	1	x − 3
Никита	x

Какую информация мы не использовали? То, что разница между расстояниями ребят равна 2 км. Возьмём этот факт для обоснования уравнения.

x = 15 км/ч — скорость Никиты.

Ответ: 15 км/ч.

Задачи на движение по прямой, по воде и по окружности — все они есть в нашем бесплатном тренажёре для подготовки к контрольным и экзаменам. Переходите по ссылкам и прокачивайте свои математические навыки легко и с удовольствием!