Сокращенное умножение: правила, формулы, примеры

Для кого эта статья:

• Студенты и школьники, изучающие математику
• Преподаватели, готовящие уроки по теме сокращенного умножения
• Все, кто хочет улучшить свои навыки в математических вычислениях

Калькулятор формул сокращенного умножения

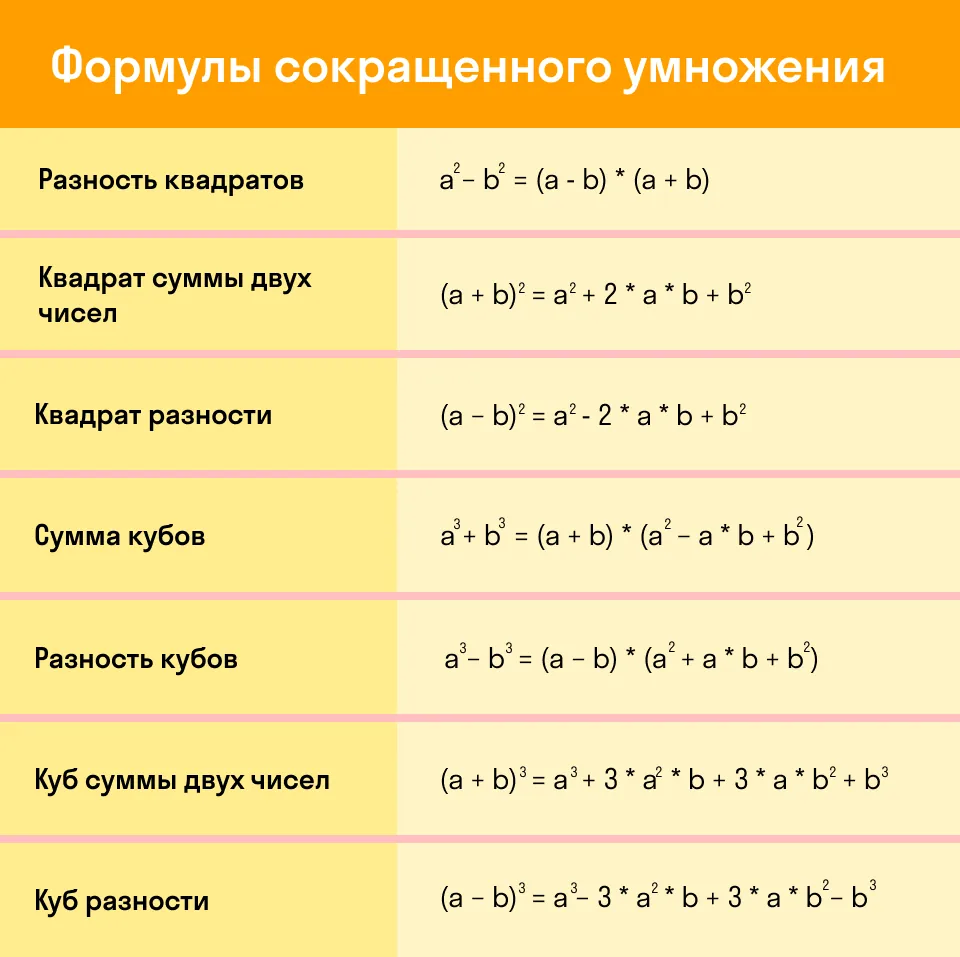
Формулы сокращенного умножения

Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.

Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.

210.1K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Прокачивай знания на курсах математики

• Выбирай из 1200+ репетиторов по математике

• Записывайся на бесплатные курсы для детей

Как читать формулы сокращенного умножения

Учимся проговаривать формулы сокращенного выражения:

 

1. Разность квадратов двух выражений равна произведению их разности и их суммы.
2. Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.
3. Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.
4. Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.
5. Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.
6. Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
7. Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.

Обучение на курсах по математике — дорога к хорошим оценкам в школе и высокому баллу на экзамене.

Доказательство формул сокращенного умножения

Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a² - b² = (a - b) * (a + b).

Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a - b) * (a + b) = a² - b².

Важно знать, что разность квадратов не равна квадрату разности: a² - b² ≠ (a - b)².

Докажем, что a² - b² = (a - b) * (a + b).

Поехали:

1. Используя искусственный метод, прибавим и отнимем одно и тоже a * b.

   + a * b - a * b = 0

   a² - b² = a² - b² + ab - ab

2. Сгруппируем иначе: a² - b² + a * b - a * b = a² - a * b + a * b - b²
3. Продолжим группировать: a² - a * b - b² +a * b = (a² - a * b) + (a * b - b²)
4. Вынесем общие множители за скобки:

   (a² - a * b) + (a * b - b²) = a *(a - b) + b *(a - b)

5. Вынесем за скобки (a - b). a * (a - b) + b * (a - b) = (a - b) * (a + b)
6. Результат доказательства: a² - b² = (a - b) * (a + b)
7. Для того, чтобы доказать в обратную сторону: (a - b) * (a + b) = a² - b², нужно раскрыть скобки: (a - b) * (a + b) = a * a + a * b - b * a - b * b = a² - b².

Остальные ФСУ можно доказать аналогичным методом.

Дополнительные формулы сокращенного умножения

К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.

Бином Ньютона

Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:

Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:

ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.

Формула возведения в квадрат суммы трех, четырех и более слагаемых

Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два. 

(a₁+a₂+…+a_n)² = a₁² + a₂² + … + a_n-1² + a_n² + 2 * a₁ * a₂ + 2 * a₁ * a₃ + 2 * a₁ * a₄ + … +

+ 2 * a₁ * a_n-1 + 2 * a₁ * a_n + 2 * a₂ * a₃ + 2 * a₂ * a₄ + … + 2 * a₂ * a_n-1 + 2 * a₂ * a_n +…+

+ 2 * a_n-1 * a_n

Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Формула разности n-ых степеней двух слагаемых

aⁿ − bⁿ = (a − b) * (a^n-1 + a^n-2 * b + a^n-3 * b² + … + a * b^n-2 + b^n-1).

Для четных показателей можно записать так:

a^2*m − b^2*m = (a² − b²) *(a^2*m−2 + a^2*m−4 * b² + a^2*m−6 * b⁴ + … + b^2*m−2).

Для нечетных показателей:

a^2*m+1 − b^2*·m+1 = (a − b) * (a^2*m + a^2*m−1 * b + a^2*m−2 * b² + … + b^2*m).

Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.

Решение задач

Давайте потренируемся и рассмотрим примеры с дробями.

Задание 1

Что сделать: вычислить квадрат произведения (55 + 10)².

Как решаем: воспользуемся формулой квадрата суммы: (55 + 10)² = 55² + 2 * 55 * 10 + 10² = 3025 + 1100 + 100 = 4225.

Задание 2

Что сделать: упростить выражение 64 * с³ – 8.

Как решаем: применим разность кубов: 64 * с³ – 8 = (4 * с)³ – 2³ = (4 * с – 2)((4 * с)² + 4 * с * 2 + 2²) = (4 * с – 2)(16 * с² + 8 * с + 4).

Задание 3

Что сделать: раскрыть скобки (7 * y - x) * (7 * y + x).

Как решаем:

1. Произведем умножение: (7 * y - x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x - x * 7 * y - x * x = 49 * y² + 7 * y * x - 7 * y * x - x² = 49 * y² - x².
2. Используем формулу сокращенного умножения: (7 * y - x) * (7 * y + x) = (7 * y)² - x² = 49 * y² - x².

Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей :)

Тест: Формулы сокращенного умножения