Что такое пирамида и из чего она состоит
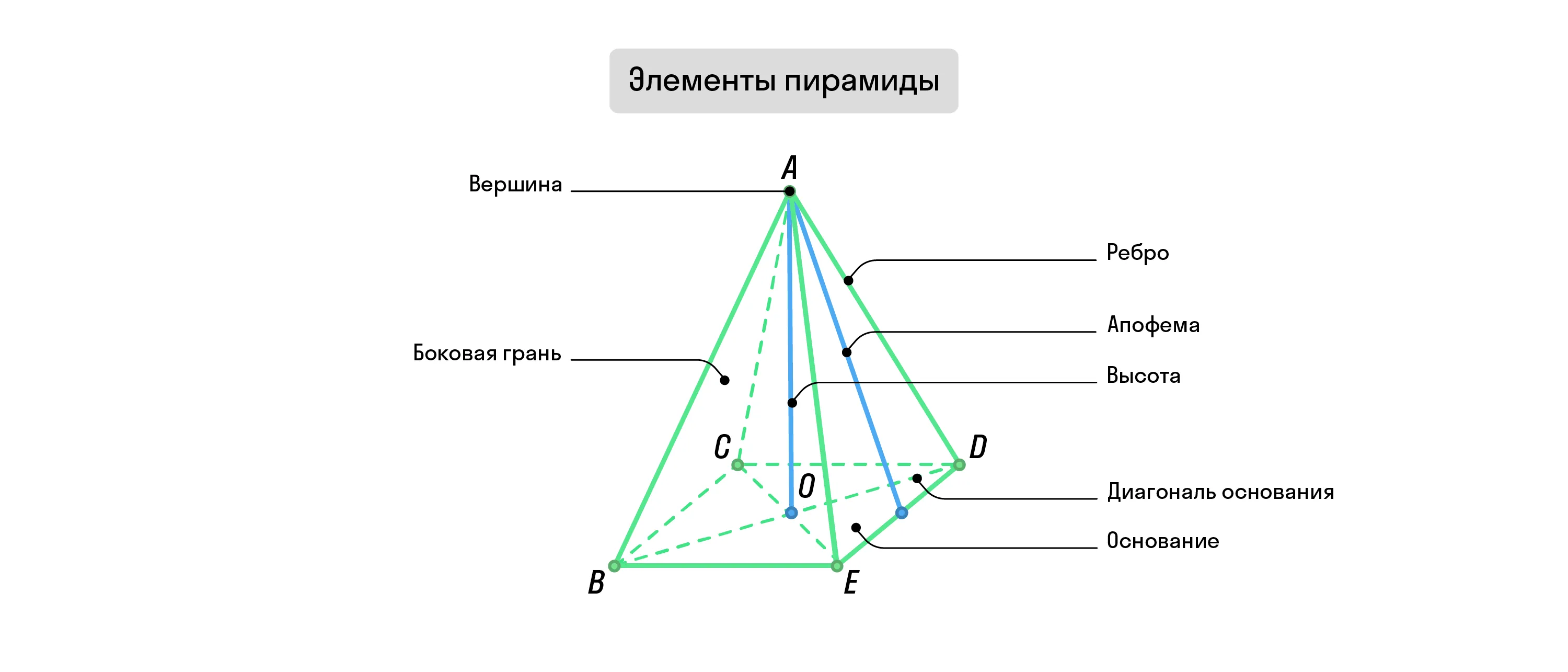
Пирамида — это многогранник, состоящий из многоугольника в основании и треугольников по бокам, которые образованы при соединении точки вершины фигуры и вершин её основания.
Те треугольники по бокам — это боковые грани пирамиды, а их общие стороны — её рёбра. Кроме того, у каждой пирамиды есть апофема — это перпендикулярная прямая, которая опущена из её вершины к стороне основания.
Высота пирамиды — это перпендикуляр, опущенный из её вершины к основанию.
В отличие от других многоугольников, у пирамиды нет диагоналей. Всё потому, что каждая вершина её основания соединена с вершиной самой фигуры и образует треугольную грань. Выходит, у пирамиды нет противоположных вершин. Зато они есть у самого основания, а значит, есть и диагонали этого основания.
Какими бывают пирамиды
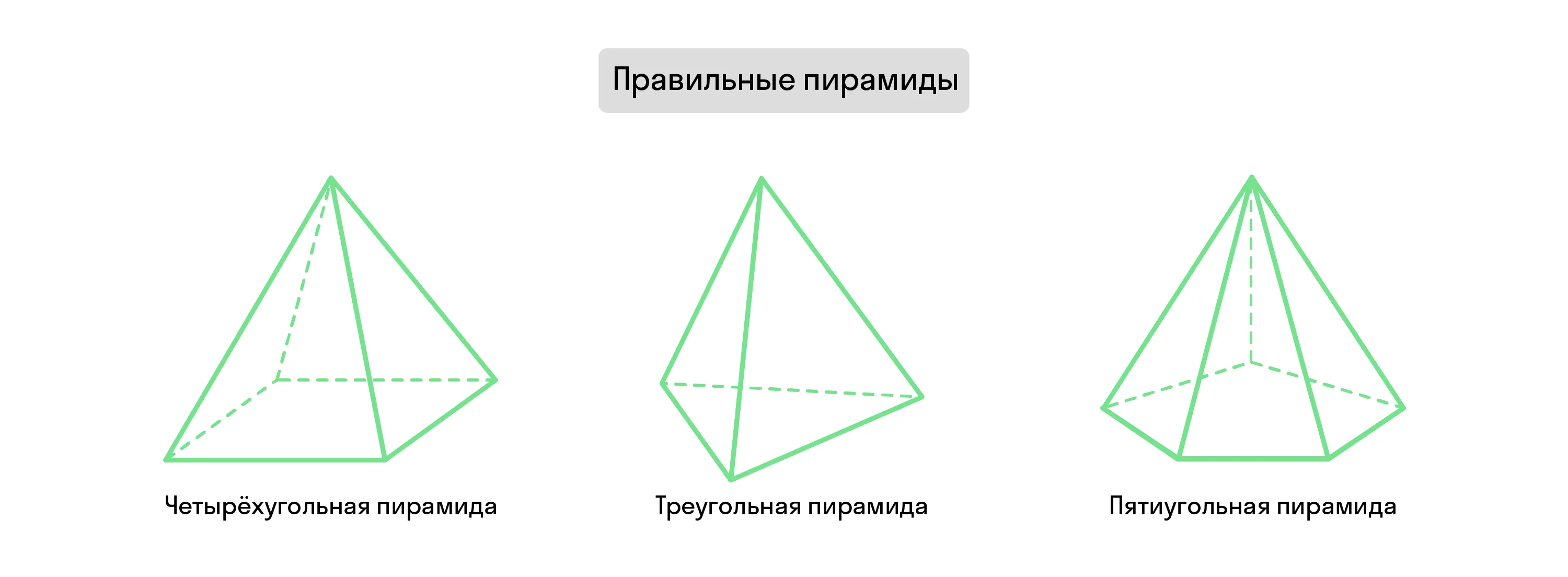
Т. к. основанием пирамиды может быть любой многоугольник, от этого зависит и тип самой фигуры. Если в её основании лежит треугольник, она будет называться треугольной. В зависимости от основания, пирамиды бывают также четырёхугольными, пятиугольными, шестиугольными и т. д.
Если в задаче неизвестно, какой именно многоугольник лежит в основании пирамиды или это не важно, условие назовёт такую пирамиду n-угольной.
Остроугольные и тупоугольные пирамиды
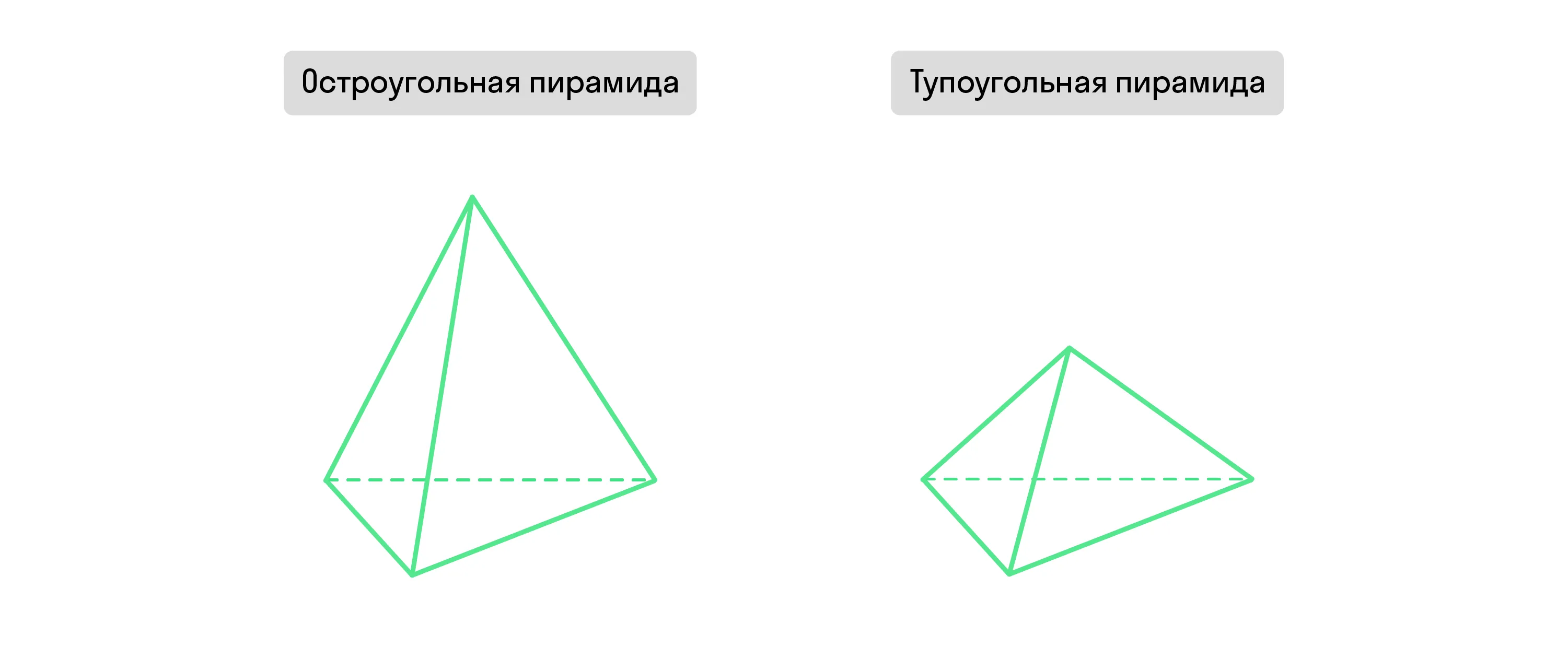
Пирамида может быть остроугольной и тупоугольной. В первом случае апофема больше длины стороны основания, во втором — меньше.
Правильные и неправильные пирамиды
Если высота пирамиды соединяет её вершину с центром основания, а оно само представляет из себя правильный многоугольник, то и пирамида называется правильной.
Все боковые грани такой фигуры — это одинаковые равнобедренные треугольники. При этом диагонали основания правильной пирамиды пересекаются в его центре и делятся им же пополам. Именно в эту точку опускается и высота этой фигуры.
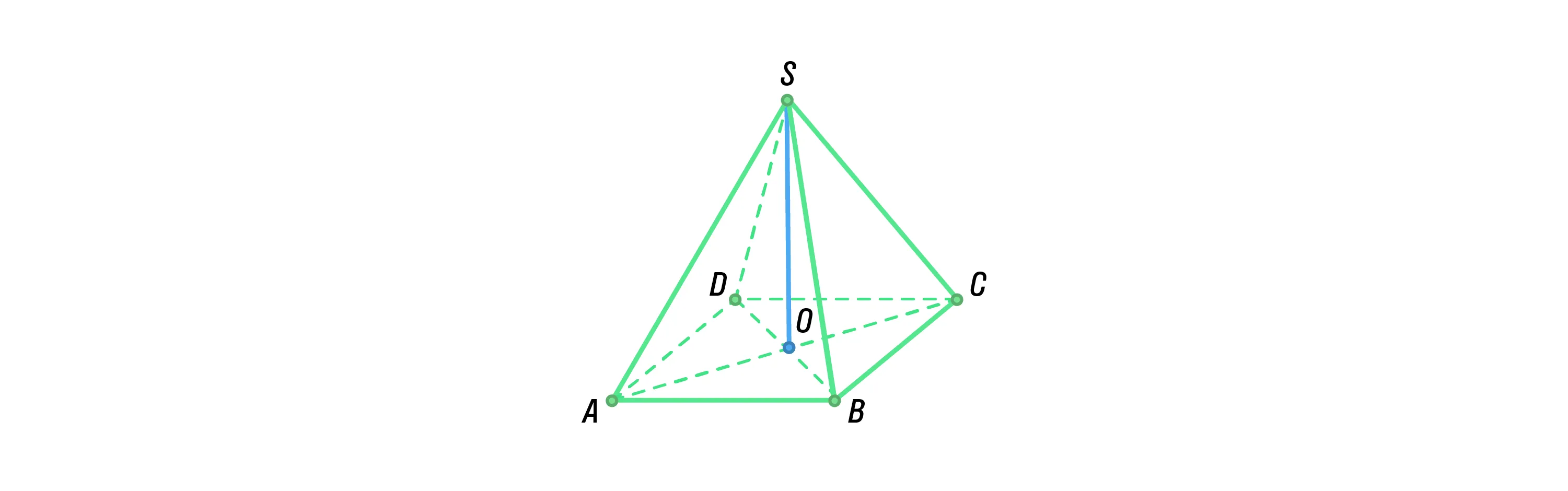
Одно из важных свойств правильной пирамиды заключается в том, что все её рёбра наклонены к её основанию под одинаковыми углами. При этом равны также длины этих рёбер и апофемы пирамиды.
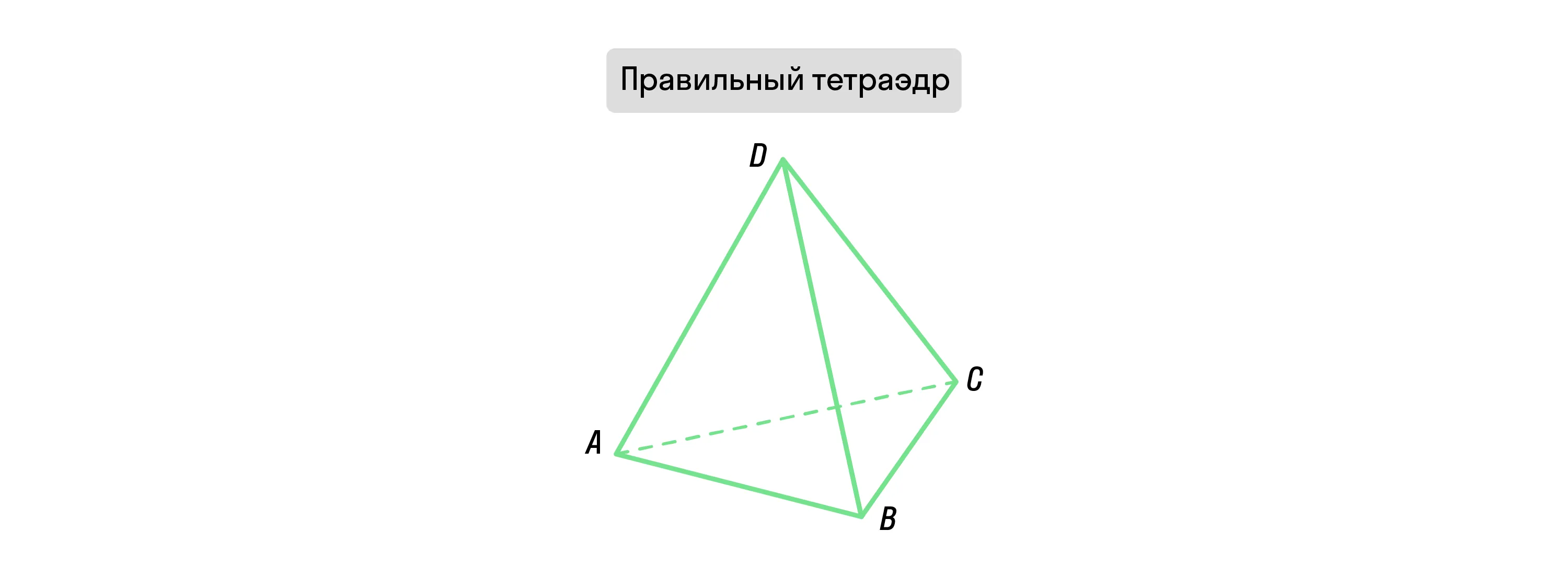
Правильный тетраэдр — это пирамида, все грани которой являются равносторонними треугольниками.
Все рёбра, грани, а также периметры и площади всех граней такой фигуры равны между собой.
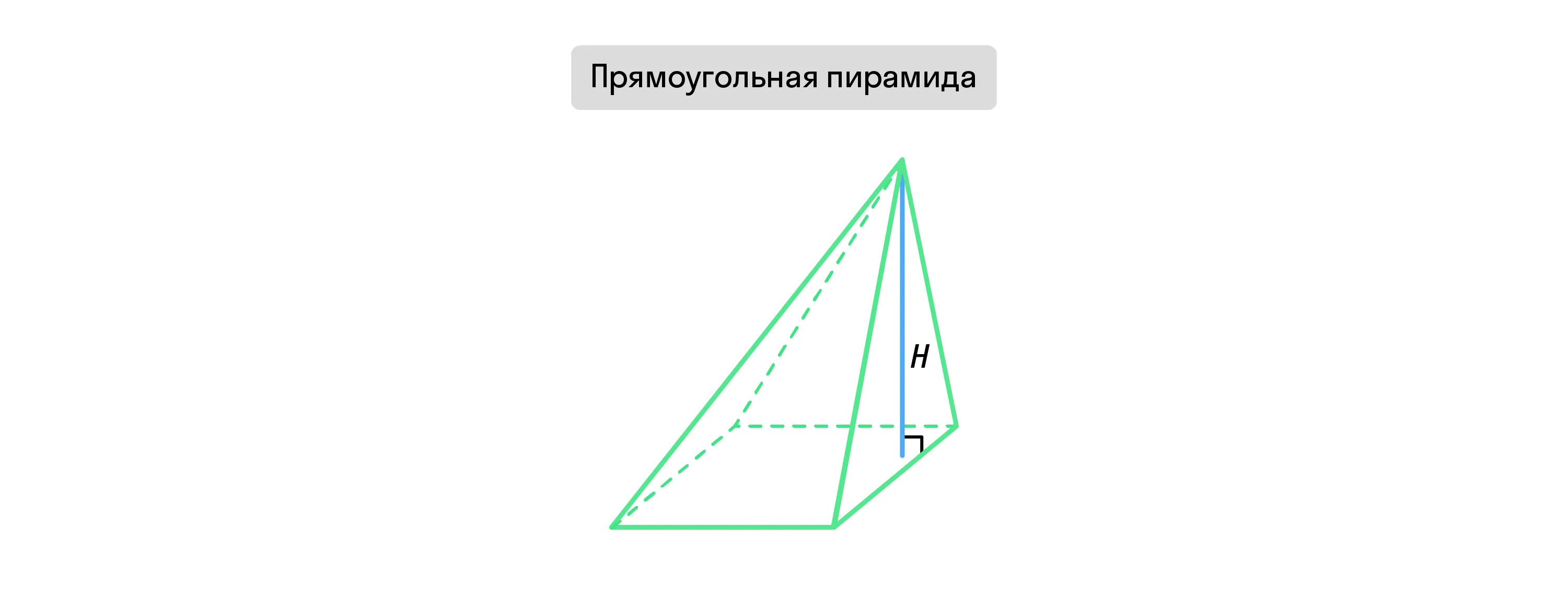
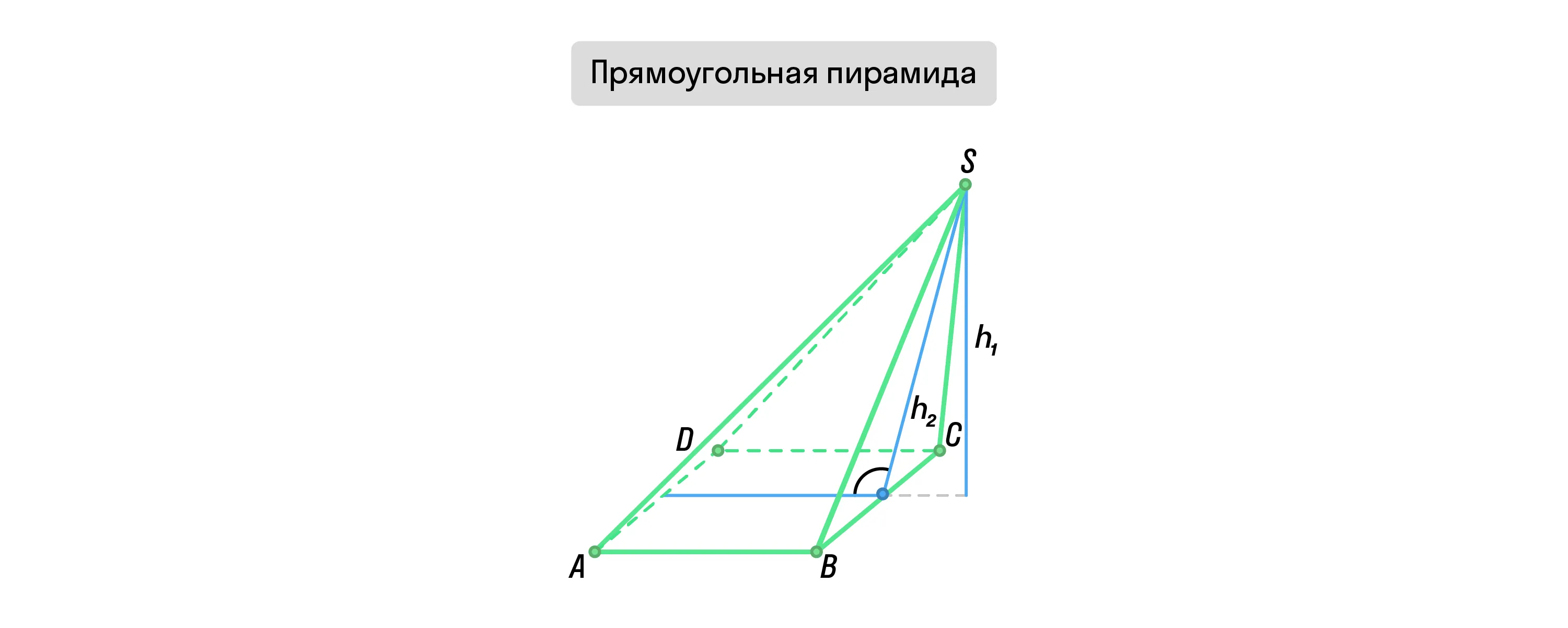
Прямоугольная пирамида
Прямоугольная пирамида — это такая пирамида, в которой одна из боковых граней перпендикулярна основанию фигуры.
У прямоугольной пирамиды проведённая высота принадлежит одной из граней. Она также равна по длине апофеме, проведённой по этой же грани.
Наклонная пирамида
Наклонная пирамида — это такая пирамида, в которой одно из рёбер образует тупой угол с основанием.
Если провести высоту такой пирамиды, она будет опущена вне основания фигуры.
Усечённая пирамида
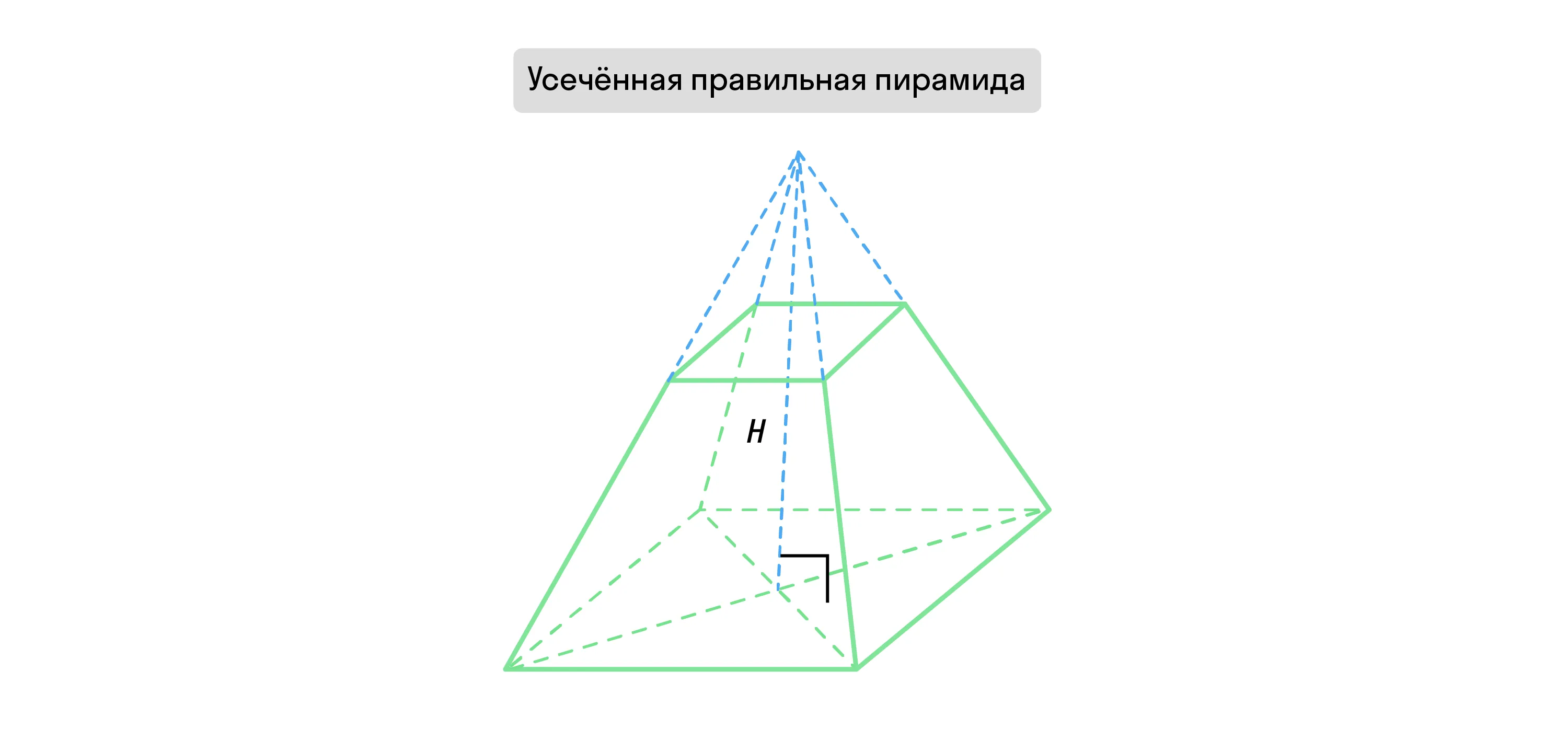
Усечённая пирамида — это нижняя часть пирамиды, которую разделяет плоскость, параллельная основанию фигуры.
Образовавшиеся так параллельные грани усечённой пирамиды считаются её основаниями. Расстояние между ними, т. е. перпендикулярная прямая, которая опущена от одного основания к другому, — это высота такой пирамиды.
В отличие от остальных видов пирамид, у усёченной есть диагонали.
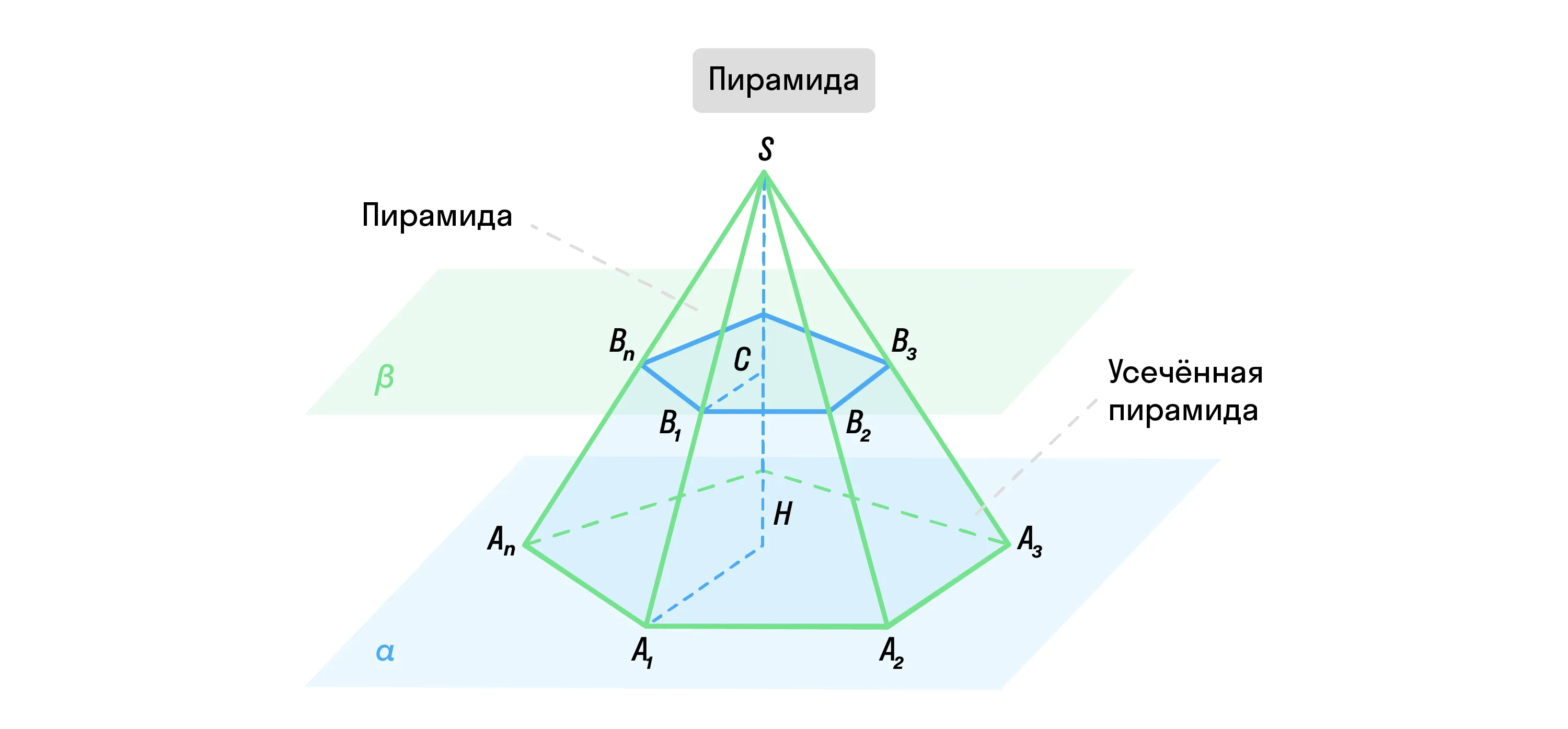
Если такая фигура была получена усечением правильной пирамиды, она называется усечённой правильной пирамидой.
Все боковые грани этой фигуры — это равнобедренные трапеции.
Получи больше пользы от Skysmart:
-
Подготовься к ОГЭ на пятёрку.
-
Подготовься к ЕГЭ на высокие баллы.
Записывайся на бесплатные курсы для детей.
Решай задания в бесплатном тренажёре ЕГЭ.
Пирамида и сфера
Вокруг пирамиды можно описать сферу, если в основании этой пирамиды лежит многогранник, вокруг которого можно описать окружность. Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых рёбер пирамиды.
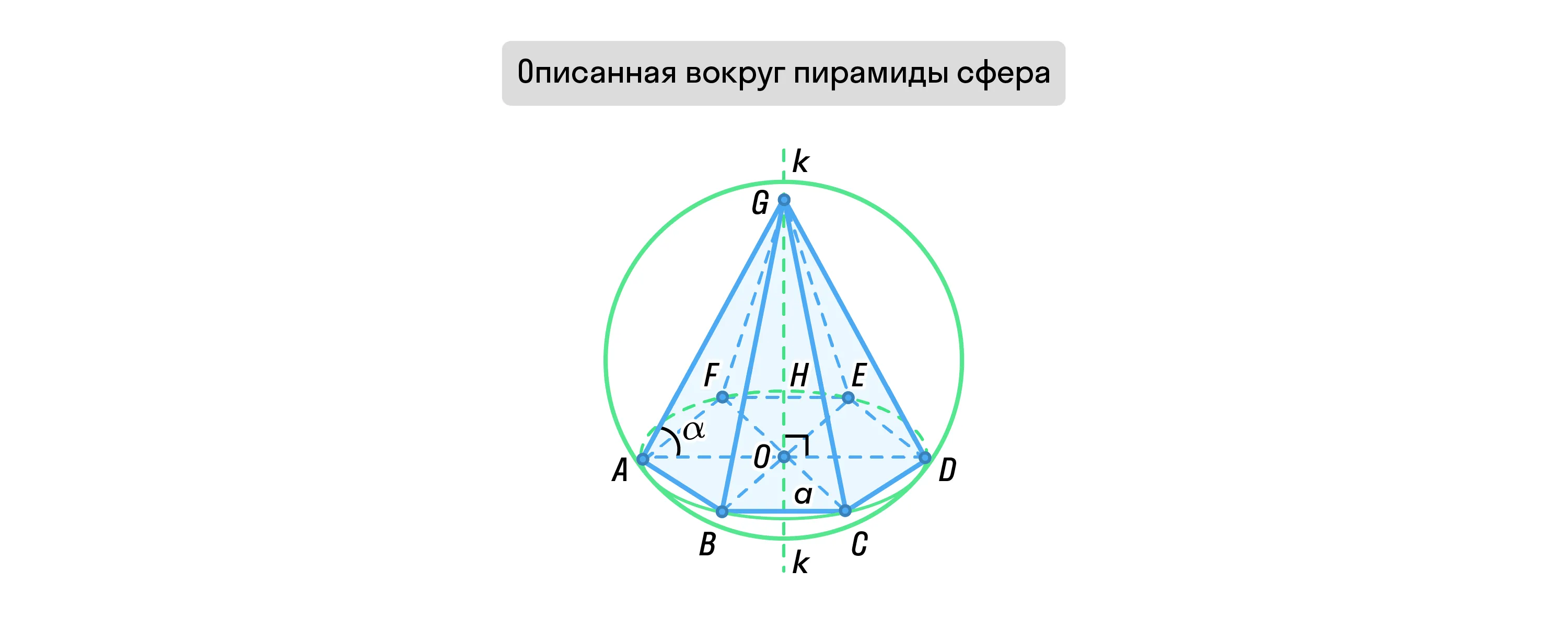
Биссекторная плоскость — это такая плоскость, которая выходит из ребра двугранного угла, которая делит его на два равных двугранных угла.
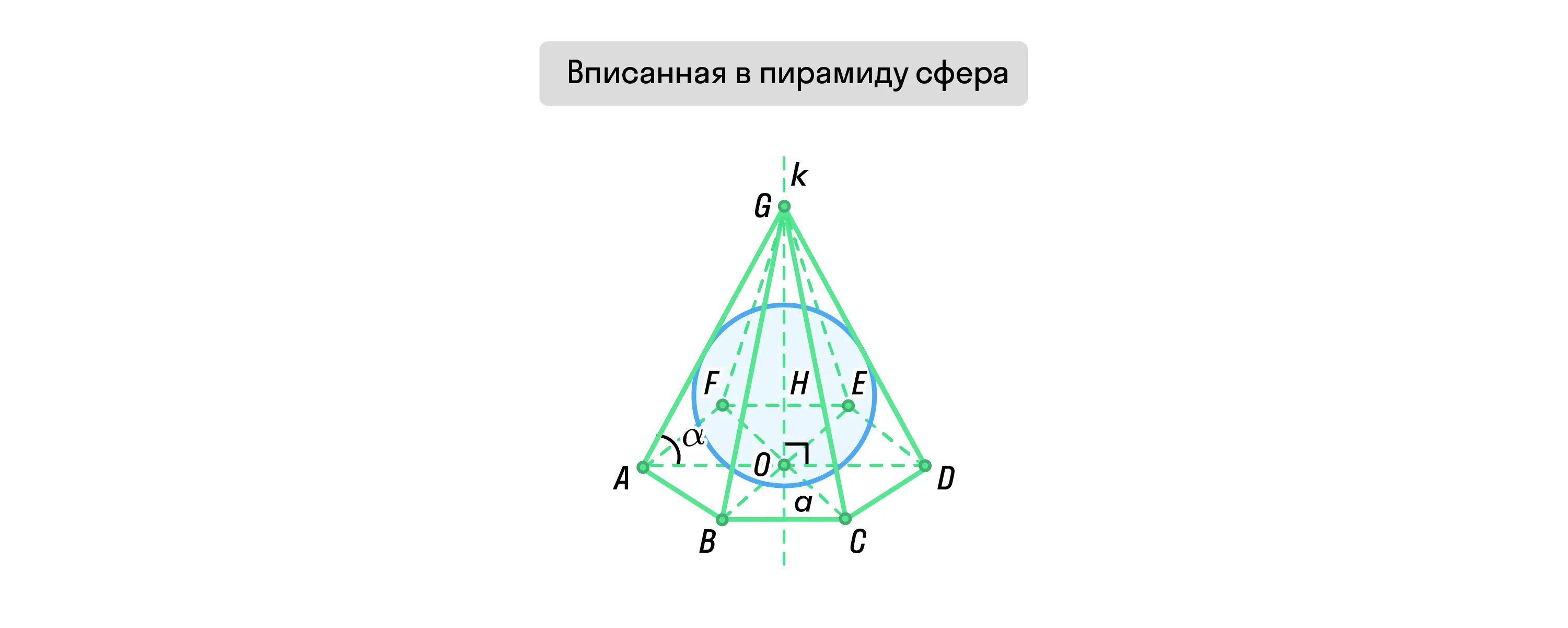
В пирамиду можно вписать сферу, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке. Эта точка и будет центром сферы.
Новое
Круглые тела
Пирамида и конус
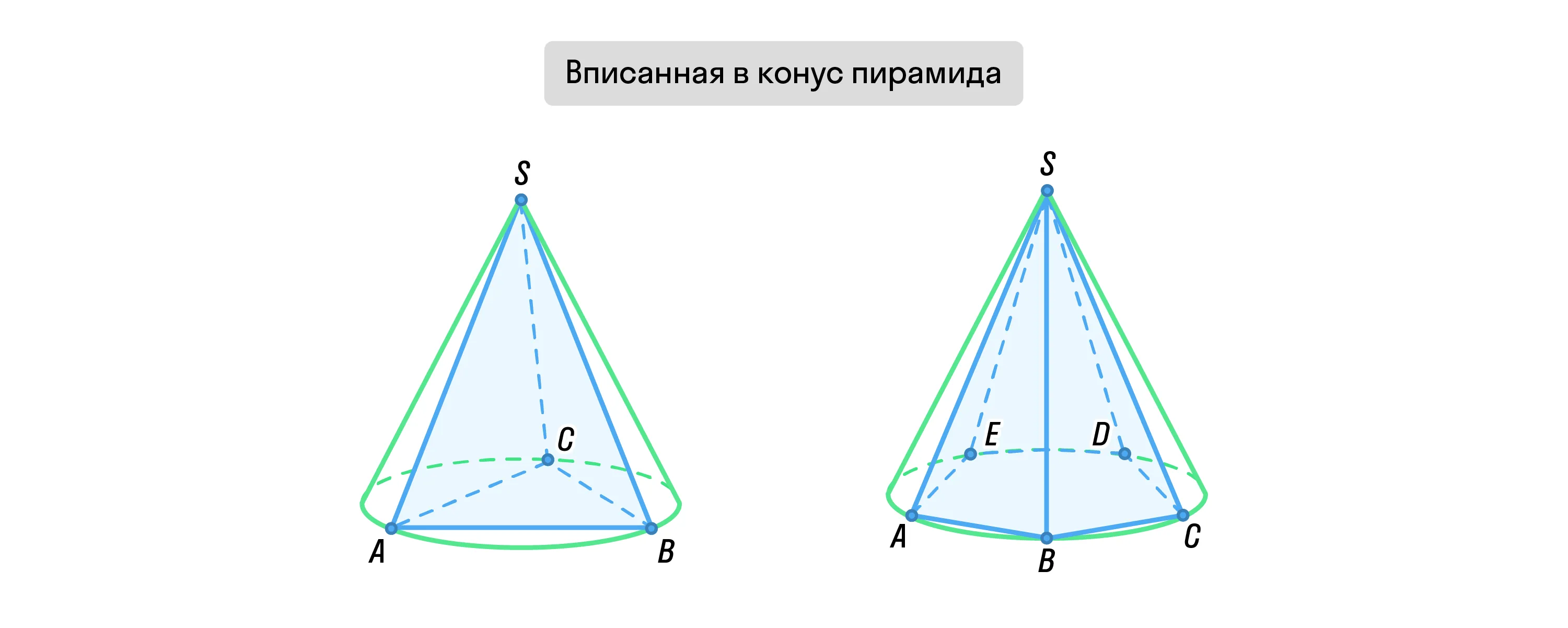
Если все боковые рёбра равны, т. е. перед нами правильная пирамида, то вокруг её основания можно описать окружность. При этом центр основания будет совпадать с центром этой окружности. Также перпендикуляр, опущенный из вершины, в этом случае будет проходить через центр основания. Это одно из условий, по которому пирамиду можно вписать в конус.
Второе условие — вершины конуса и пирамиды должны совпадать.
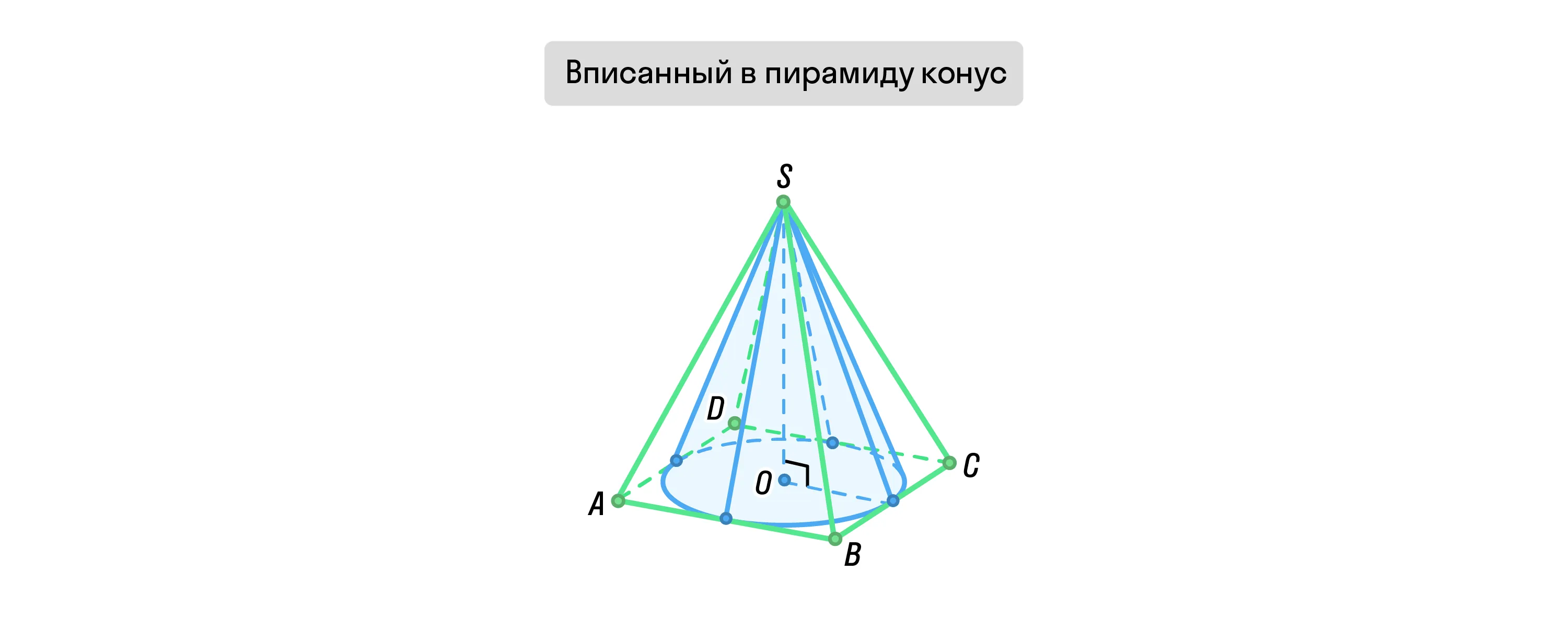
Также конус можно вписать в пирамиду. Но только в том случае, если совпадают их вершины, основание конуса вписано в основание пирамиды, а апофемы этой пирамиды равны между собой.
Пирамида и цилиндр
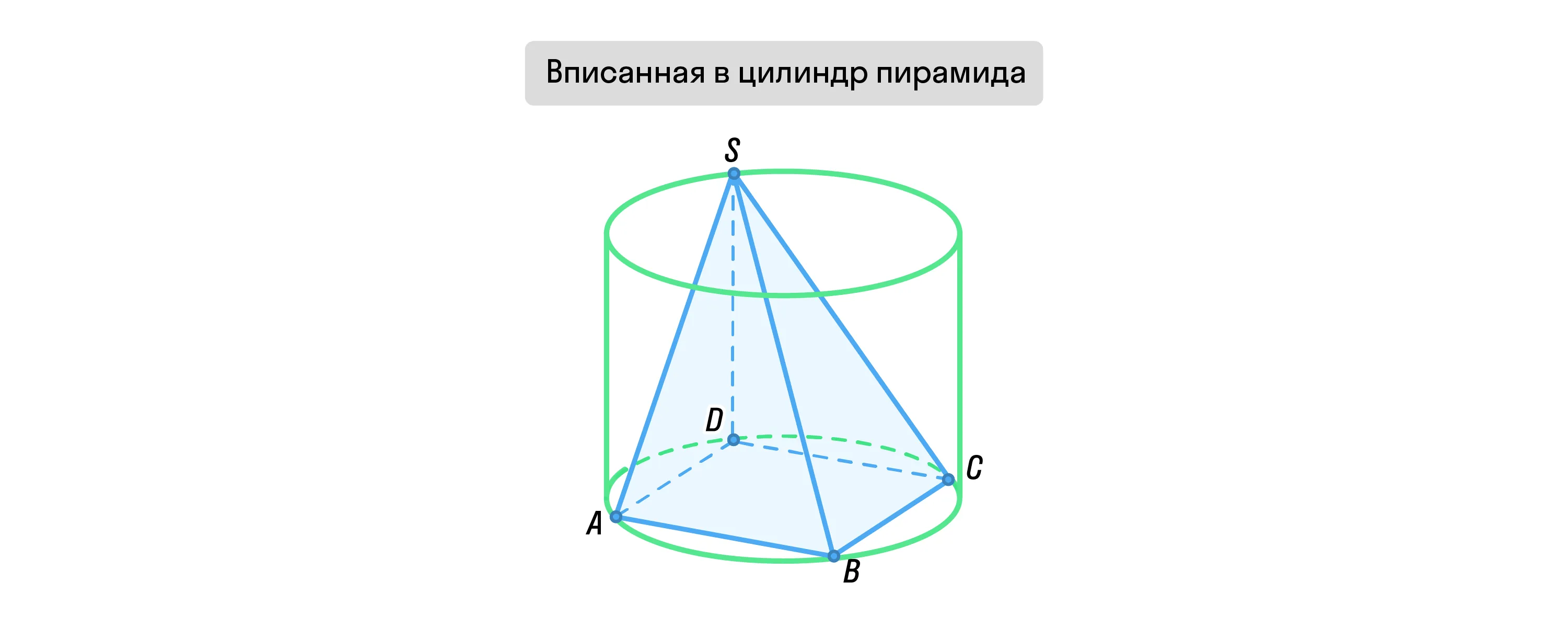
Пирамида называется считается вписанной в цилиндр, если её вершина расположена на одном из оснований цилиндра, а основание самой пирамиды вписано в другое основание цилиндра.
При этом высота вписанной пирамиды равна высоте цилиндра.
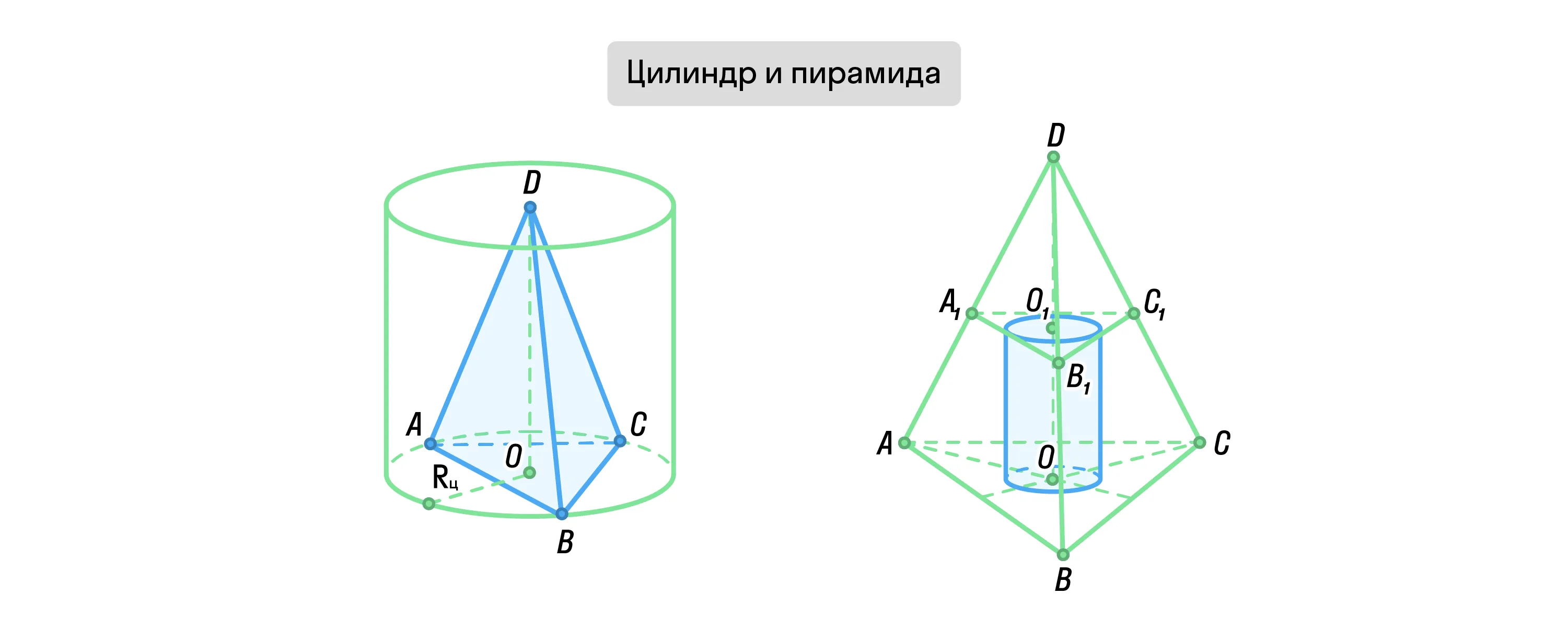
Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью, вписанной в сечение пирамиды плоскостью, параллельной основанию. Другое же основание должно быть вписанным в основание пирамиды.
Сечения пирамиды
Если пирамиду пересекает плоскость, параллельная её основанию, то и самое сечение будет подобно многоугольнику, который лежит в этом основании.
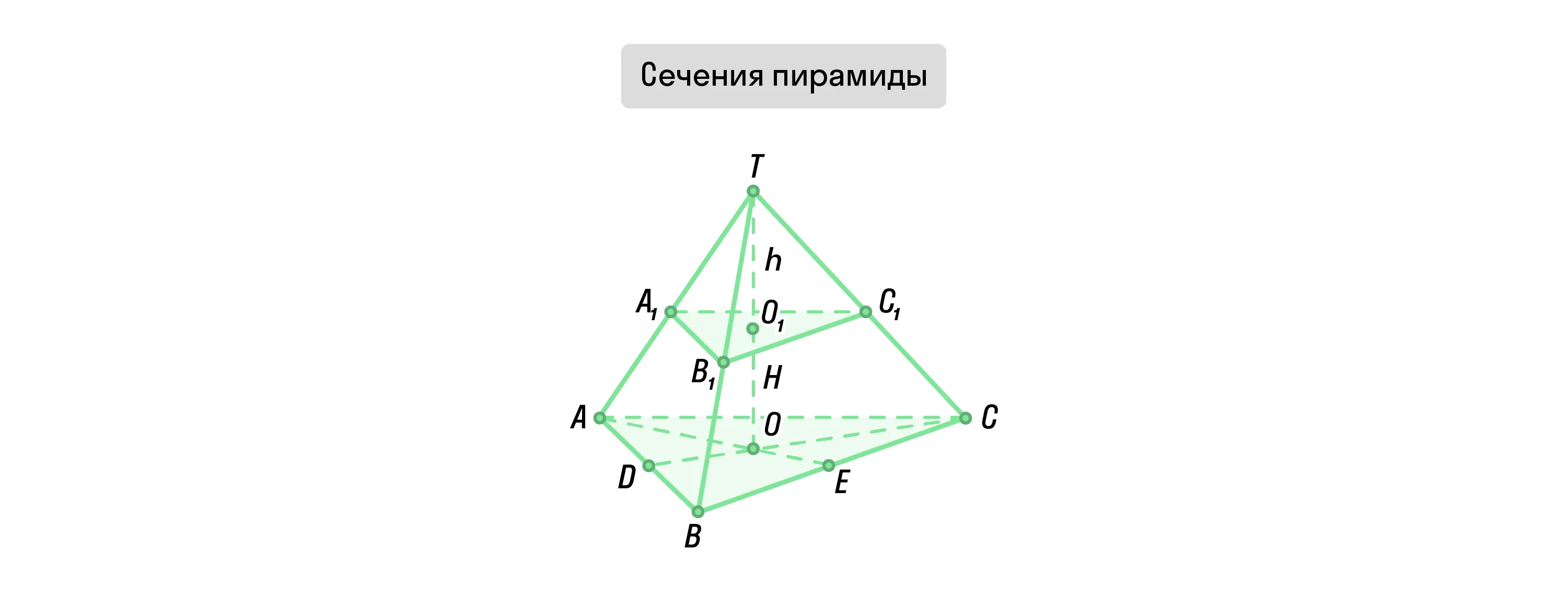
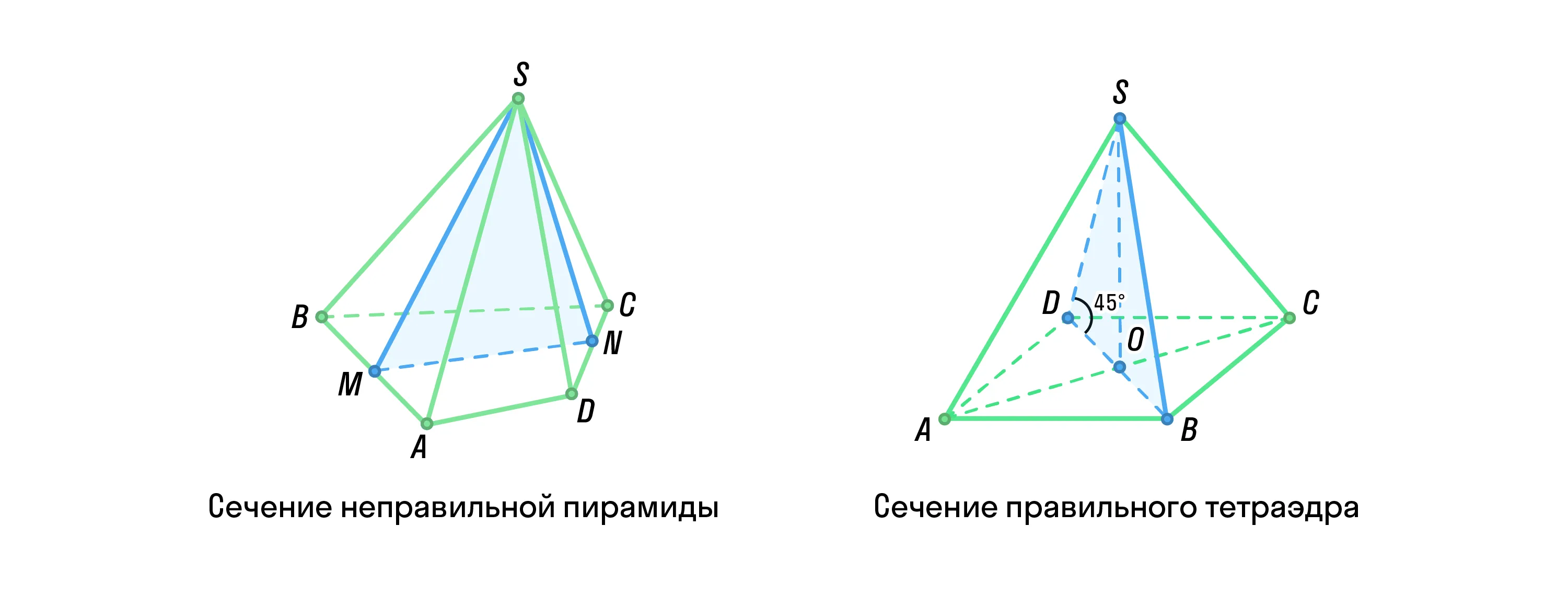
Если пирамиду пересекает плоскость, которая проходит через вершину фигуры по её высоте и перпендикулярна основанию, сечение будет треугольником. В случае с правильной пирамидой — равнобедренным, а с правильным тетраэдром — равносторонним.
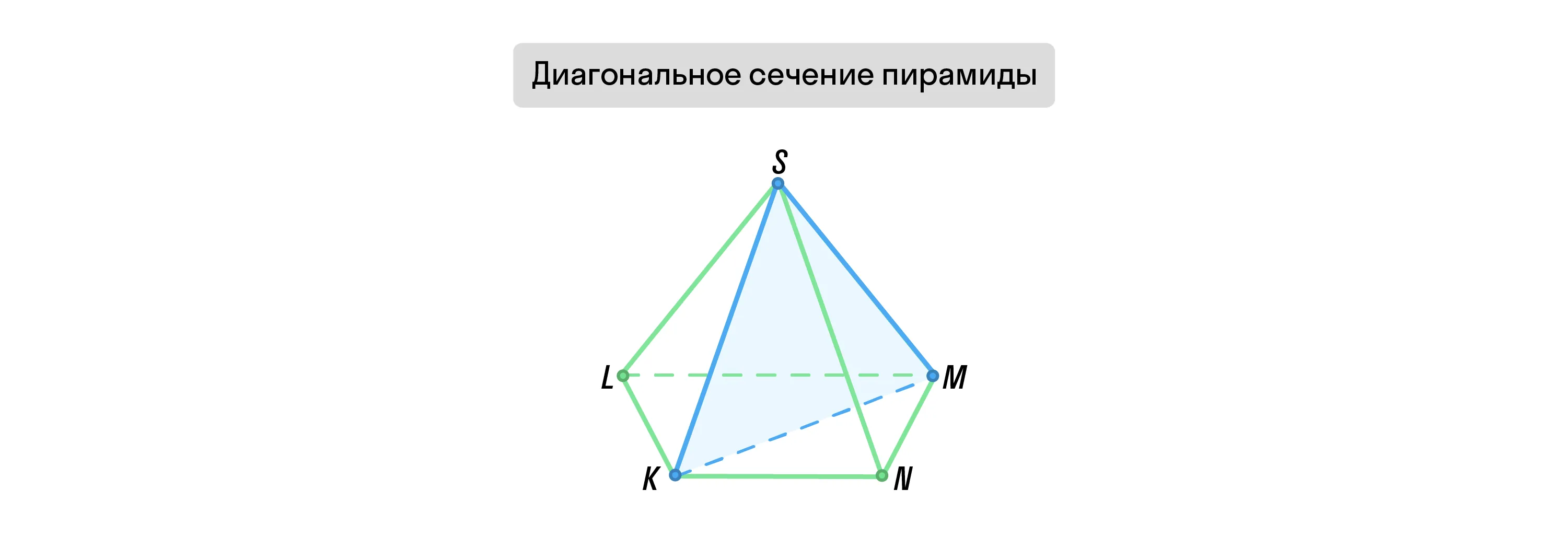
Если пирамиду пересекает плоскость, которая проходит через вершину фигуры и диагональ её основания, это сечение также будет треугольником. Такие сечения называют диагональными.
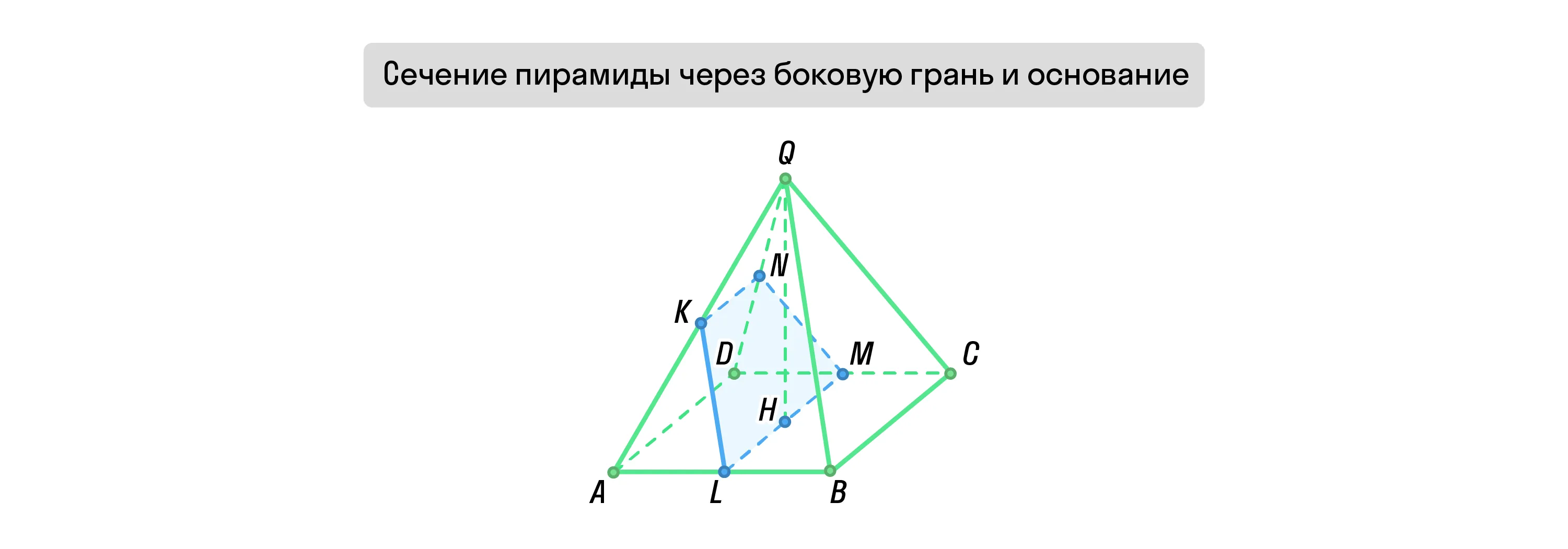
Если пирамиду пересекает плоскость, которая проходит через одну из её боковых граней и основание, такое сечение будет трапецией. В случае с правильной пирамидой трапеция будет равнобедренной.
Все формулы для решения задач с пирамидами
|
Пирамида: все формулы |
|
|---|---|
|
Объём пирамиды через площадь основания и высоту |
|
|
Площадь боковой поверхности правильной пирамиды через периметр основания и апофему |
|
|
Площадь полной поверхности пирамиды через площади боковой поверхности и основания |
|
|
Площадь боковой поверхности правильной усечённой пирамиды через периметры оснований и апофему |
|
|
Объём правильной усечённой пирамиды через площади оснований и апофему |
|
|
Радиус сферы, вписанной в правильную пирамиду, через объём пирамиды и площадь её полной поверхности |
|
|
Радиус сферы, описанной около правильной треугольной пирамиды, через высоту пирамиды и длину ребра её основания |
|
|
Радиус сферы, описанной около правильного тетраэдра, через его высоту и длину ребра основания |
|
|
Радиус сферы, описанной около правильной четырёхугольной пирамиды, через высоту пирамиды и длину ребра её основания |
|
|
Радиус сферы, описанной около правильной шестиугольной пирамиды, через высоту пирамиды и длину ребра её основания |
|
Узнайте, хорошо ли вы усвоили тему и можете решать экзаменационные задания с помощью Тренажёра ЕГЭ. Это сборник всех типов заданий с автопроверкой ответов, доступный бесплатно 24/7. В нём можно отточить решение задач по одной проблемной теме или написать полноценный пробный экзамен по математике.
