Куб: формулы и свойства

Что такое куб и из чего он состоит

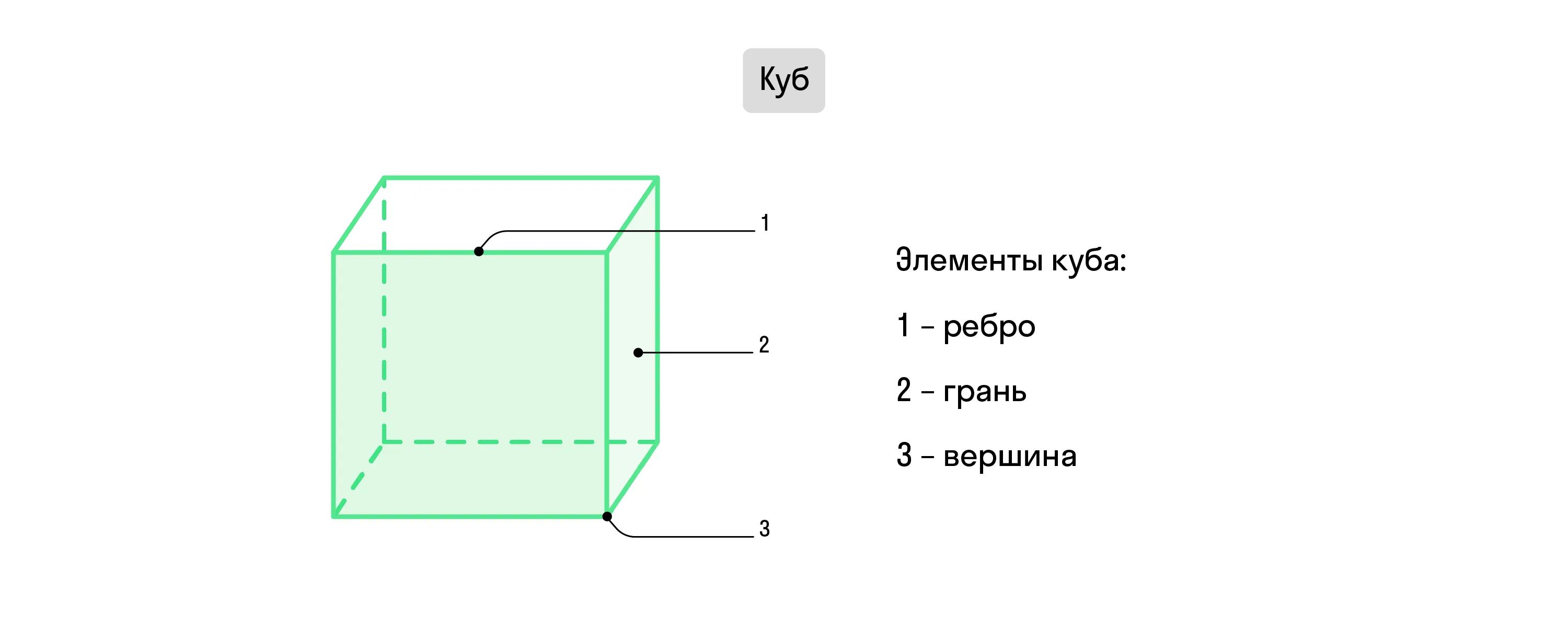
Куб или гексаэдр — это правильный многогранник с 6 одинаковыми сторонами, каждая из которых — квадрат.

Эти стороны называются гранями. Каждая грань куба пересекается с 4 другими под углом 90° и параллельна оставшейся. А т. к. все они — равные квадраты, то грани куба имеют одинаковую площадь, и их стороны, т. е. рёбра куба, равны между собой.

Точки, где они сходятся, называют вершинами куба. Всего у куба 8 вершин, и в каждой сходятся по 3 ребра.

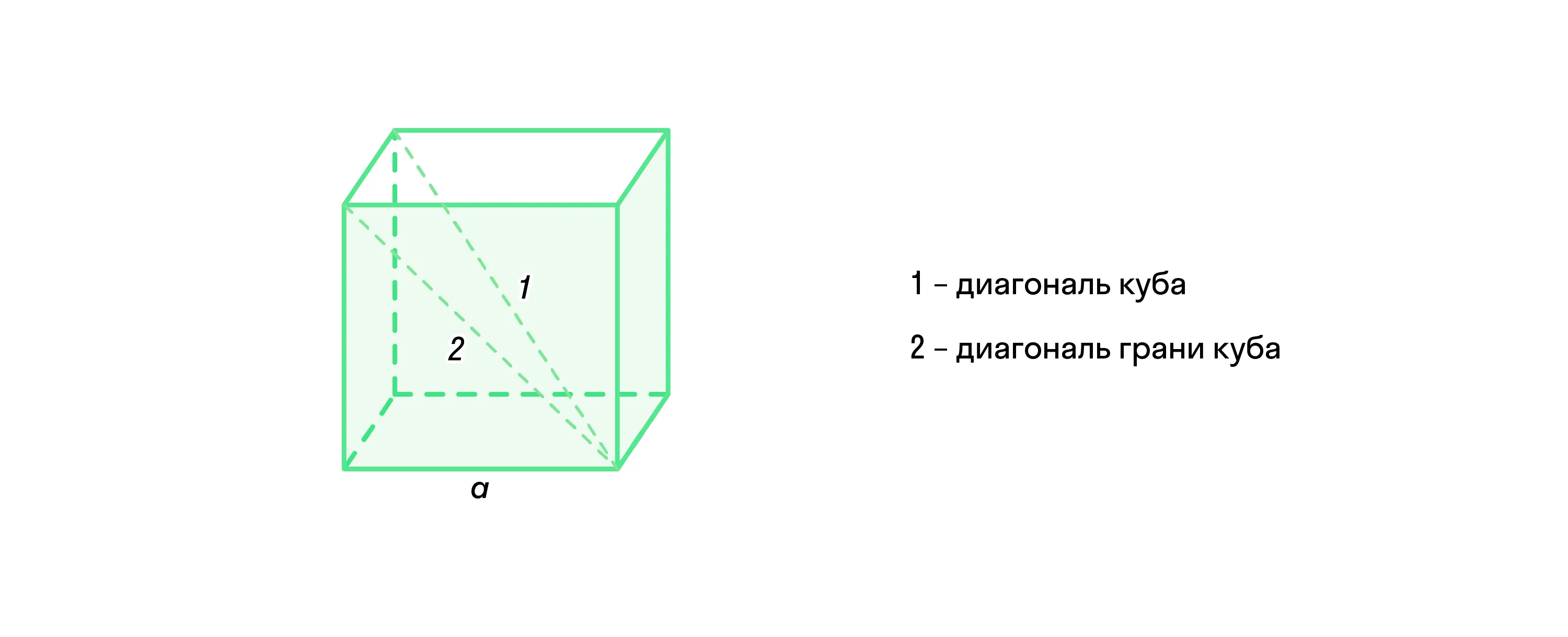
Диагональ куба — это отрезок, который соединяет противоположные вершины куба.

Всего у куба 4 диагонали. При этом они равны между собой, пересекаются в центре куба и делятся им пополам.

Также диагональ есть у каждой грани фигуры. В этом случае отрезок находится в её плоскости и соединяет противоположные вершины каждой из сторон-квадратов. Они также равны между собой и пересекаются в центре грани.

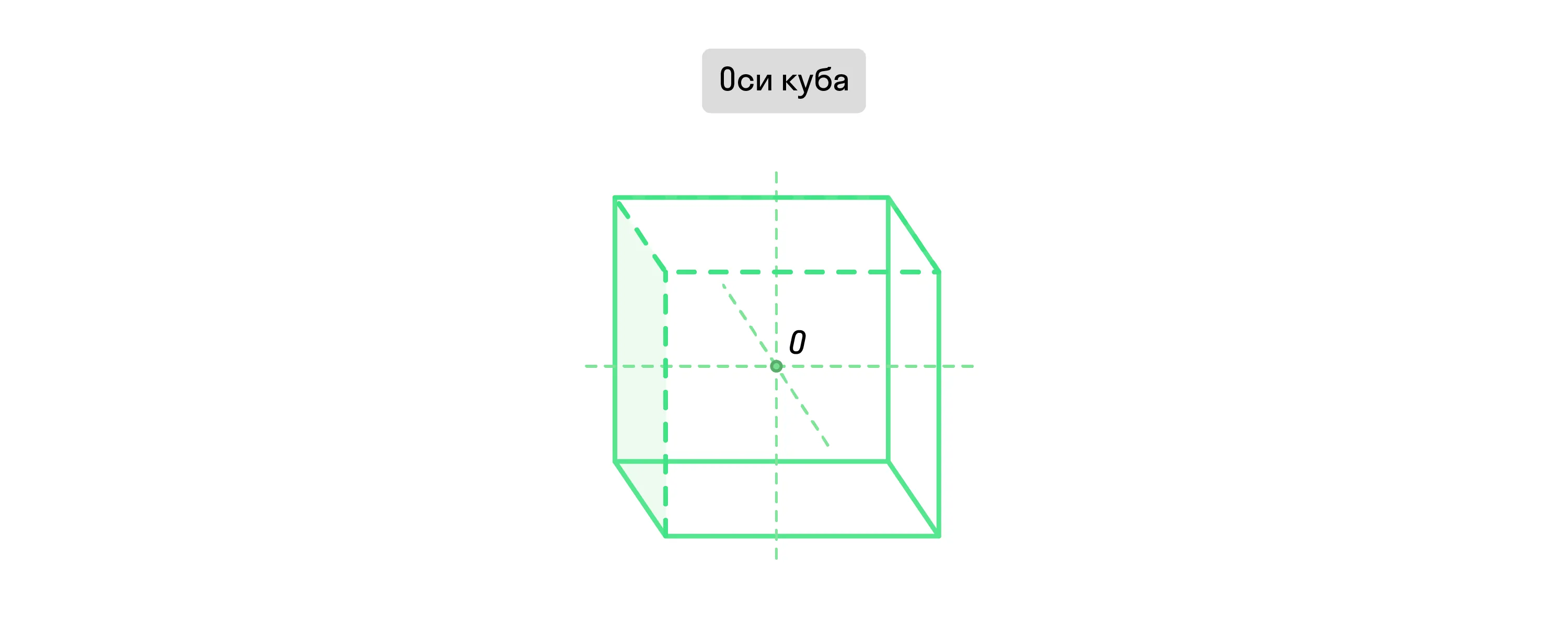
Ось куба — это прямая, которая проходит через центр куба и центры его двух параллельных между собой граней.

У каждого куба есть 3 оси, и все они взаимно перпендикулярны.

Площадь поверхности, периметр и объём куба

Площадь поверхности куба — это сумма площадей всех его граней.

При решении задач можно найти её так, а можно быстрее — через формулу S = 6a, где а — это длина ребра куба.

Пример:

Если а = 10, то S = 6a² = 6 ⋅ 10² = 6 ⋅ 100 = 600.

Периметр куба — это сумма длин всех рёбер куба.

Т. к. у куба 12 рёбер, для решения задач с периметром можно воспользоваться формулой P = 12a, где а — это длина ребра куба.

Пример:

Если а = 10, то P = 12a = 12 ⋅ 10 = 120.

Объём куба — это совокупность всех точек в пространстве, ограниченных гранями этого куба.

Иначе говоря, это вместимость трёхмерной фигуры. Чтобы вычислить её, перемножают длины рёбер многогранника, но т. к. у куба все рёбра равны, достаточно использовать формулу V = a.

Пример:

Если а = 10, то V = a³ = 10³ = 1 000.

Также объём куба можно вычислить по длине его диагонали. Тогда можно применить формулу .

170K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Куб и сфера

Вписанная в куб сфера — это такая сфера, центр которой совпадает с центром куба и которая касается центров его граней.

При этом все 6 граней куба являются касательными плоскостями к вписанной сфере, а её радиус равен половине длины ребра a.

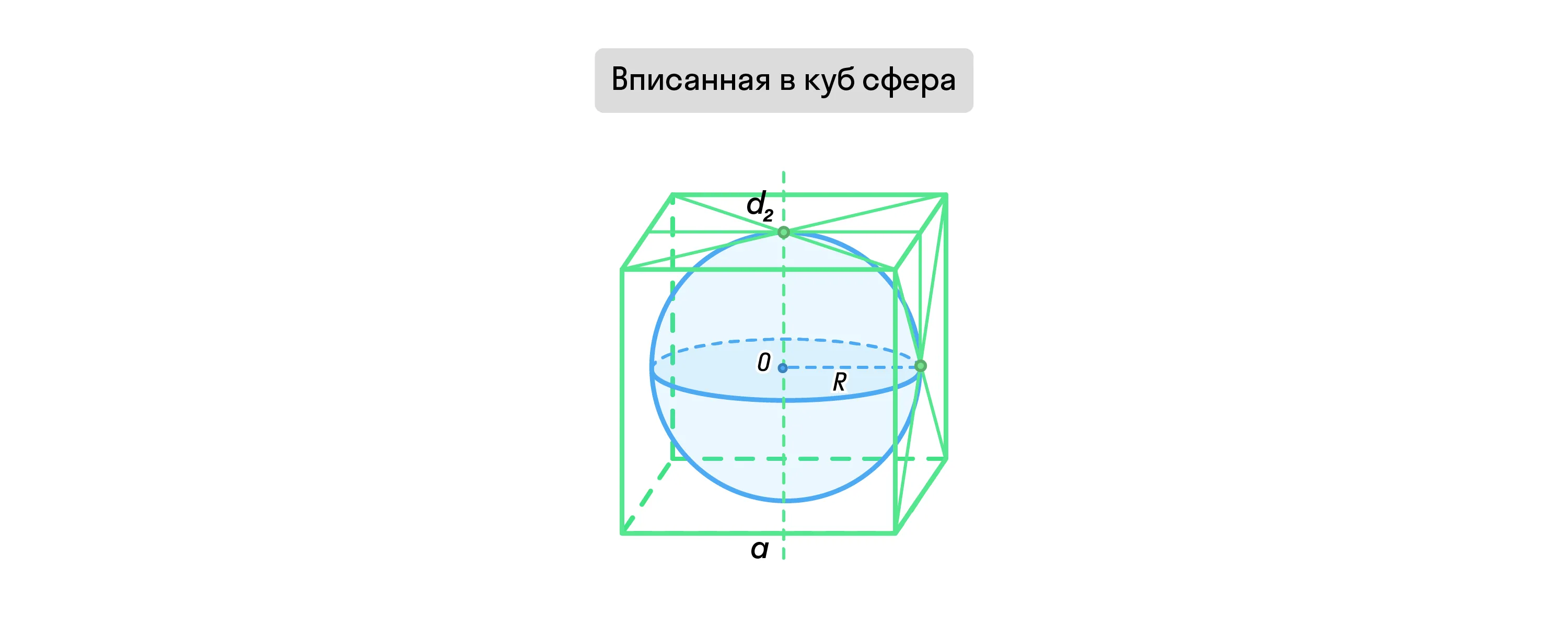
Описанная вокруг куба сфера — это такая сфера, центр которой совпадает с центром куба и которая соприкасается с 8 вершинами куба.

Радиус такой сферы равен половине длины диагонали куба.

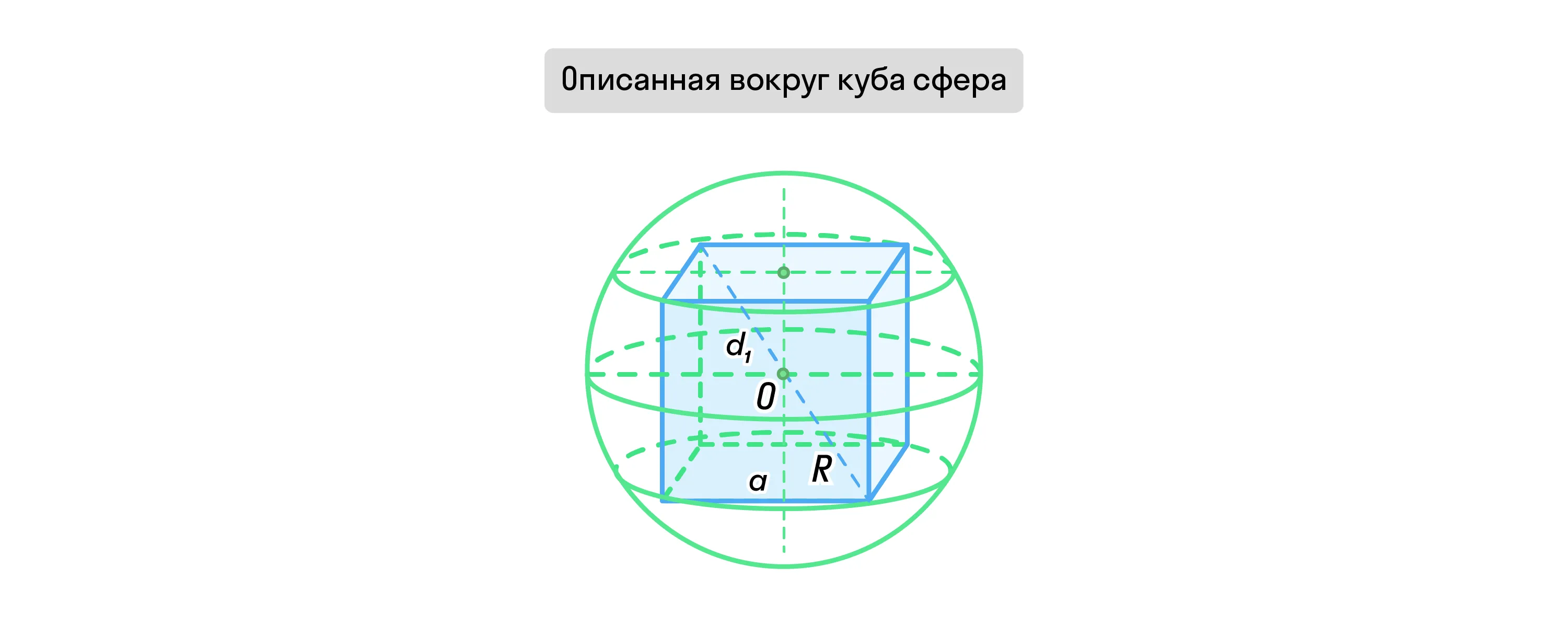
Свойства куба

В куб можно вписать тетраэдр так, чтобы все 4 вершины тетраэдра совпадали с 4 вершинами куба, а все 6 ребер тетраэдра располагались на 6 соответствующих гранях куба. При этом рёбра будут равны диагонали грани куба.

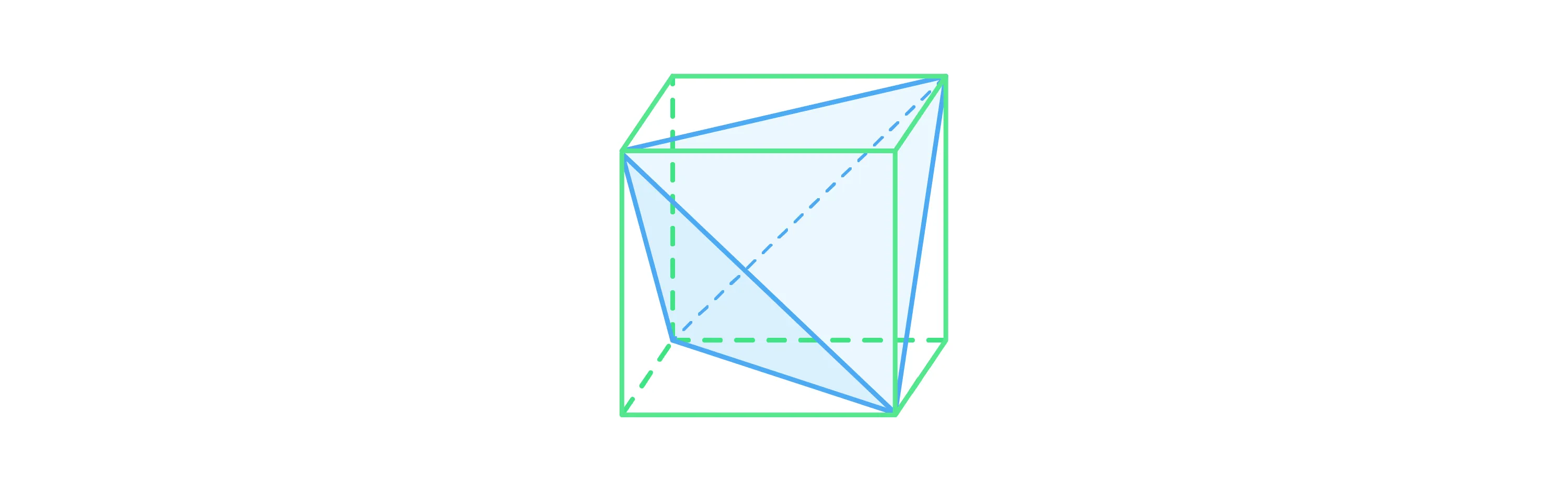
Ещё одно важное свойство куба состоит в том, что в него можно вписать правильный шестиугольник так, что все 6 вершин будут располагаться в центрах граней куба.

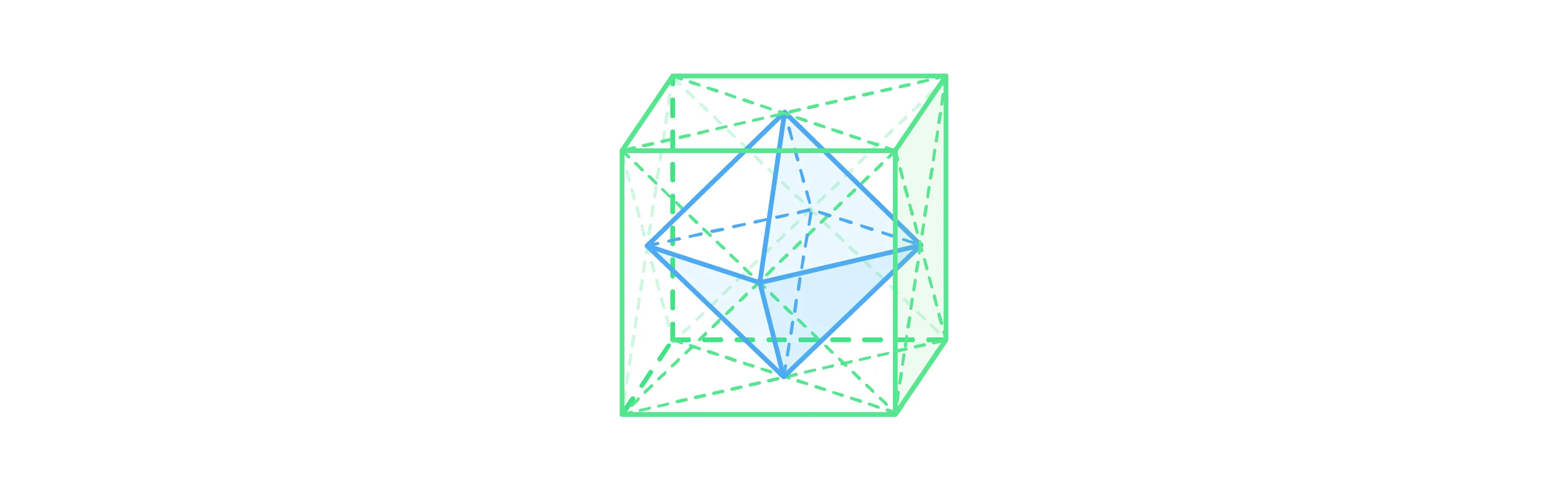
Координаты вершин куба

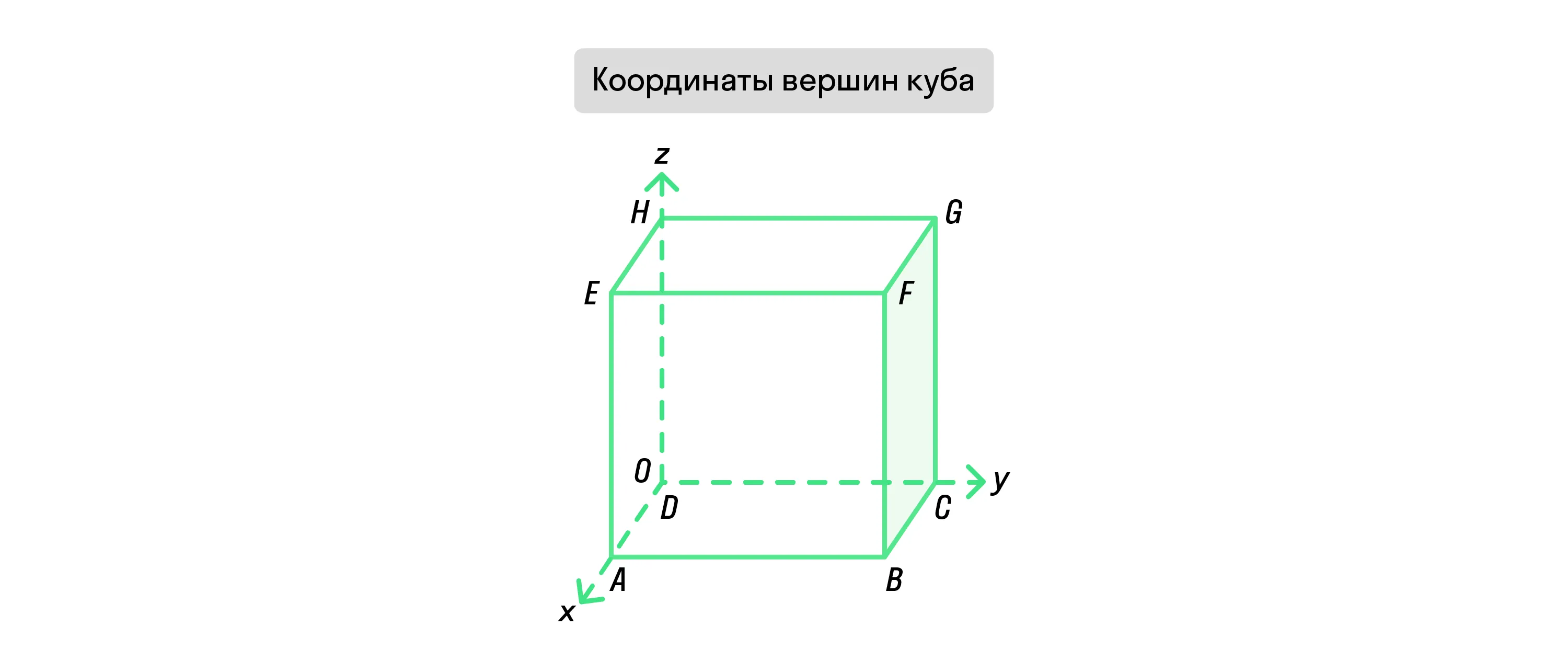
Куб — это фигура в трёхмерном пространстве, и у каждой её точки есть место на системе координат. Если куб расположен в начале этой системы так, что рёбра этой вершины лежат на осях координат, тогда его вершины будут иметь такие координаты:

A(a, 0, 0), B(a, a, 0), C(0, a, 0), D(0, 0, 0),
E(a, 0, a), F(a, a, a), G(0, a, a), H(0, 0, a),

где А, B, C, D, E, F, G и H — вершины куба, а — длина его ребра. При этом вершина D находится в начале системы координат.

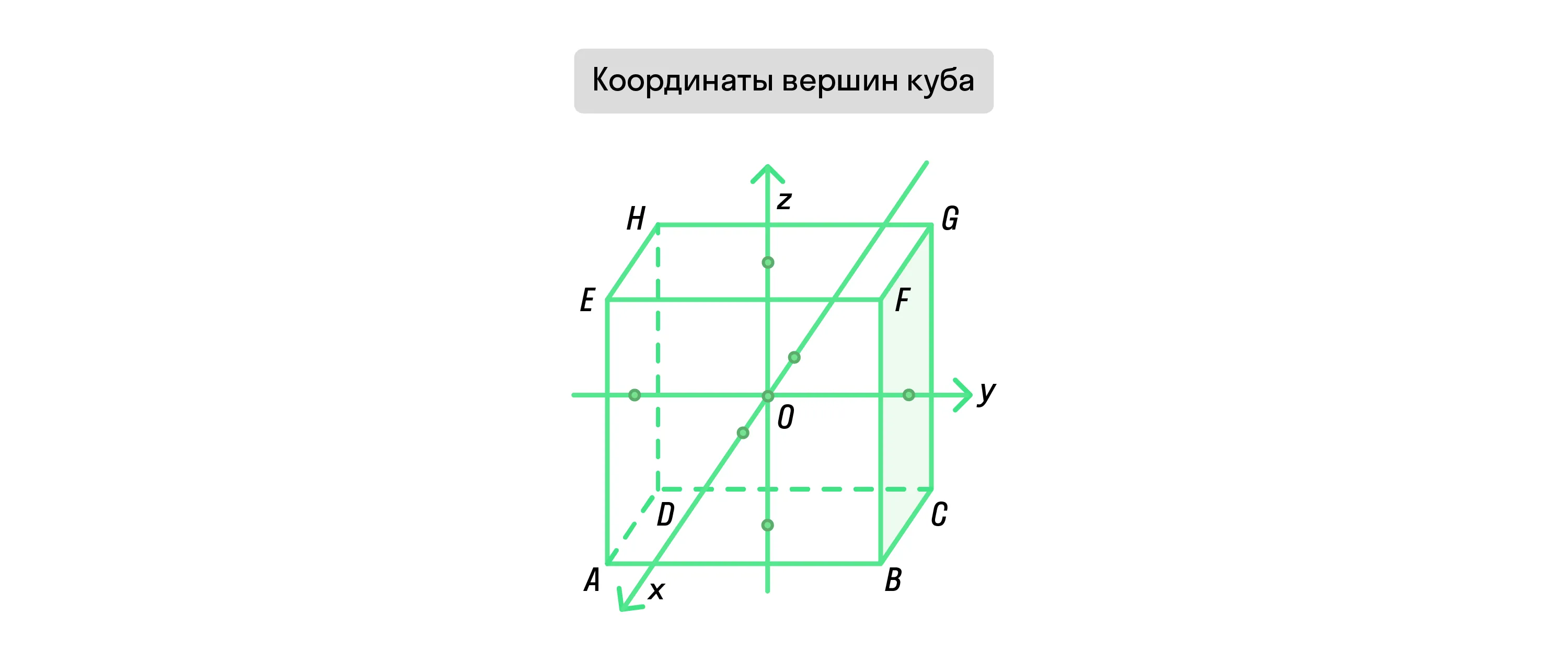
Если же куб расположен так, что начало системы координат совпадает с центром фигуры, а рёбра параллельны осям координат, тогда координаты вершин куба с длиной ребра 2a будут выглядеть так:

A(a, −a, −a), B(a, a, −a), C(−a, a, −a), D(−a, −a, −a),

E(a, −a, a), F(a, a, a), G(−a, a, a), H(−a, −a, a).

Единичный куб — это такой куб, все рёбра которого имеют длину, равную единице.

При этом гранью такого куба будет единичный квадрат со сторонами 1:1:1:1. Представим, что на рисунке, где начало системы координат совпадает с вершиной D, изображён такой куб. Тогда координаты его вершин будут такими:

A(1, 0, 0), B(1, 1, 0), C(0, 1, 0), D(0, 0, 0),
E(1, 0, 1), F(1, 1, 1), G(0, 1, 1), H(0, 0, 1).

Пересечение куба плоскостью

Если куб пересекает плоскость, которая проходит через его центр и центры двух его противоположных граней, то в сечении будет квадрат. При этом длина стороны этого квадрата будет равна длине ребра куба.

Такая плоскость делит куб на 2 одинаковых прямоугольных параллелепипеда.

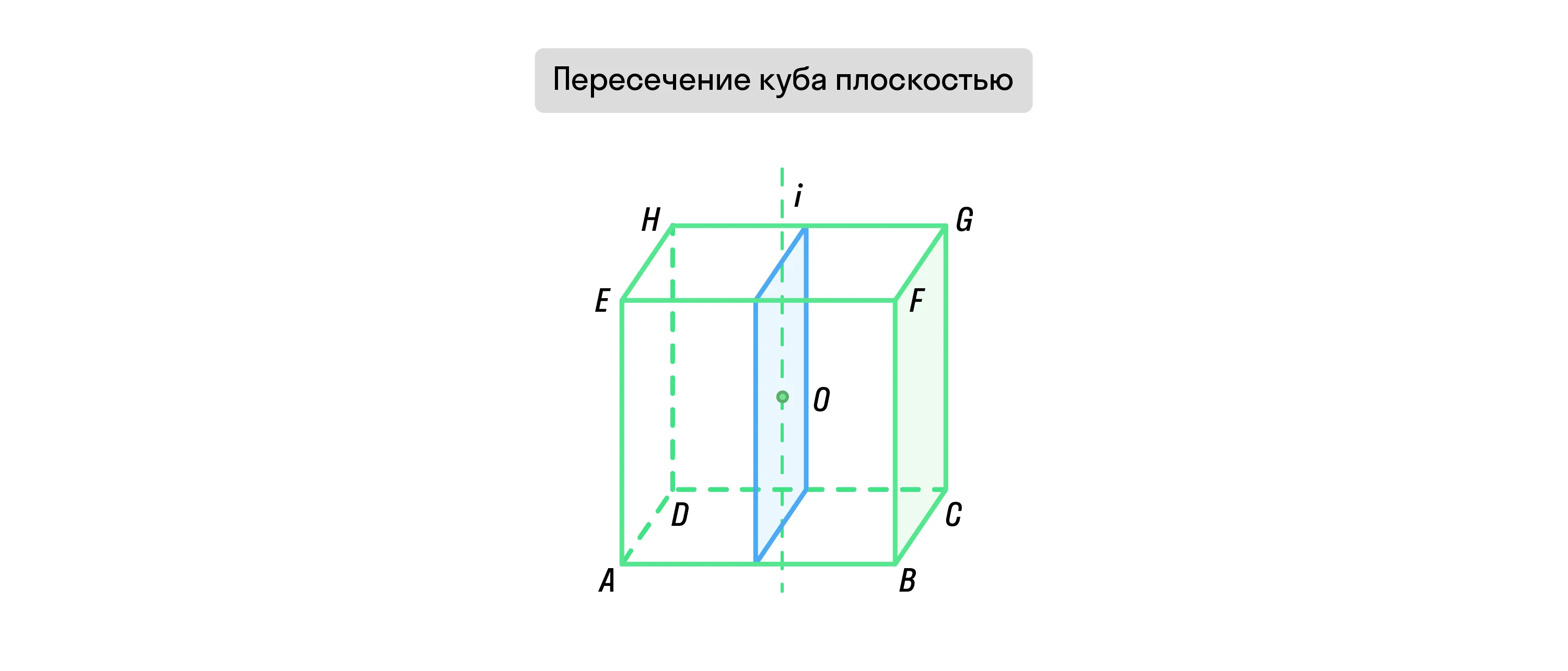
Если куб пересекает плоскость с ребром a, которая проходит через центр этого куба и два его параллельных ребра, то в сечении будет прямоугольник. Его стороны будут равны a и a√2, а площадь сечения — a2√2.

Такая плоскость делит куб на 2 одинаковые призмы.

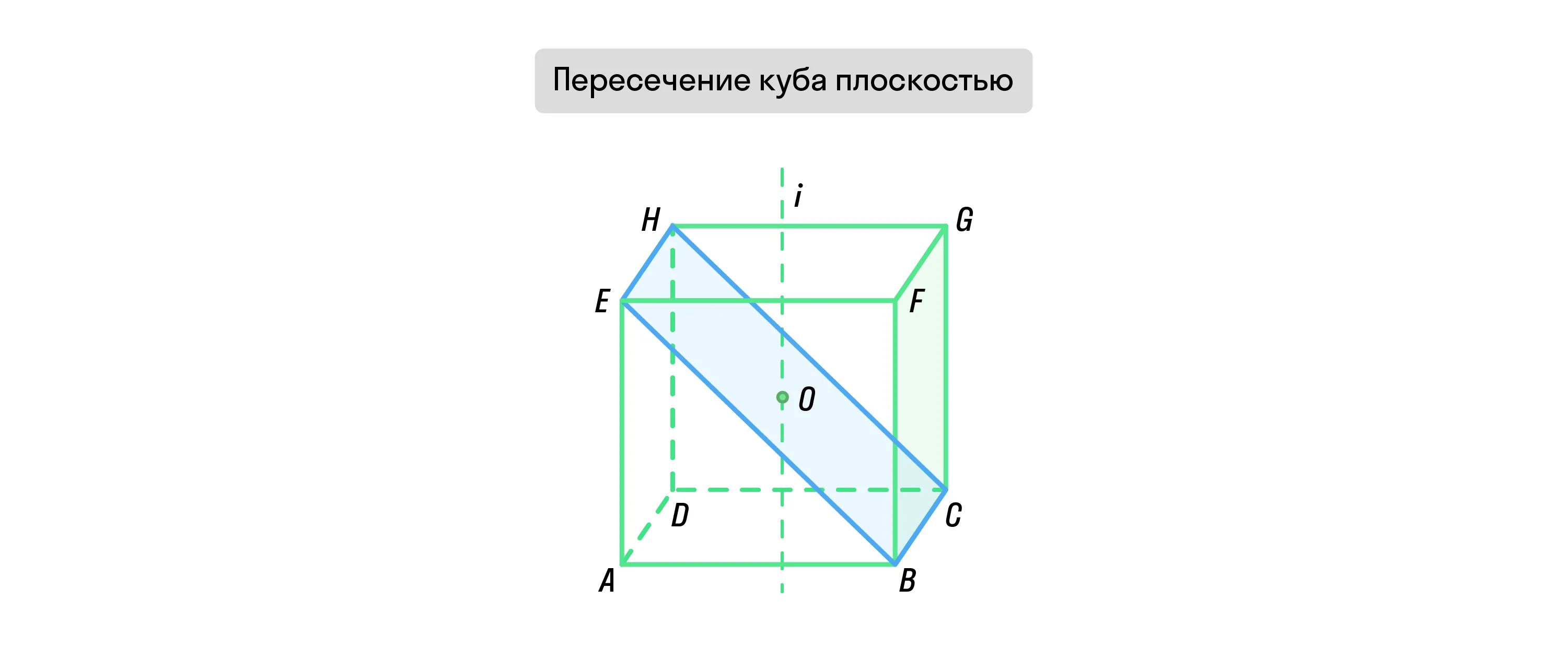
Если куб пересекает плоскость, которая проходит через 3 его вершины, то в сечении будет правильный треугольник. Его сторона будет равна a√2, площадь сечения — a²√3/2, объём большей части — 5a³/6, а меньшей — a³/6.

Одна из диагоналей куба тогда будет перпендикулярна плоскости сечения, пройдёт через центр треугольника и будет делиться плоскостью в отношении 2:1.

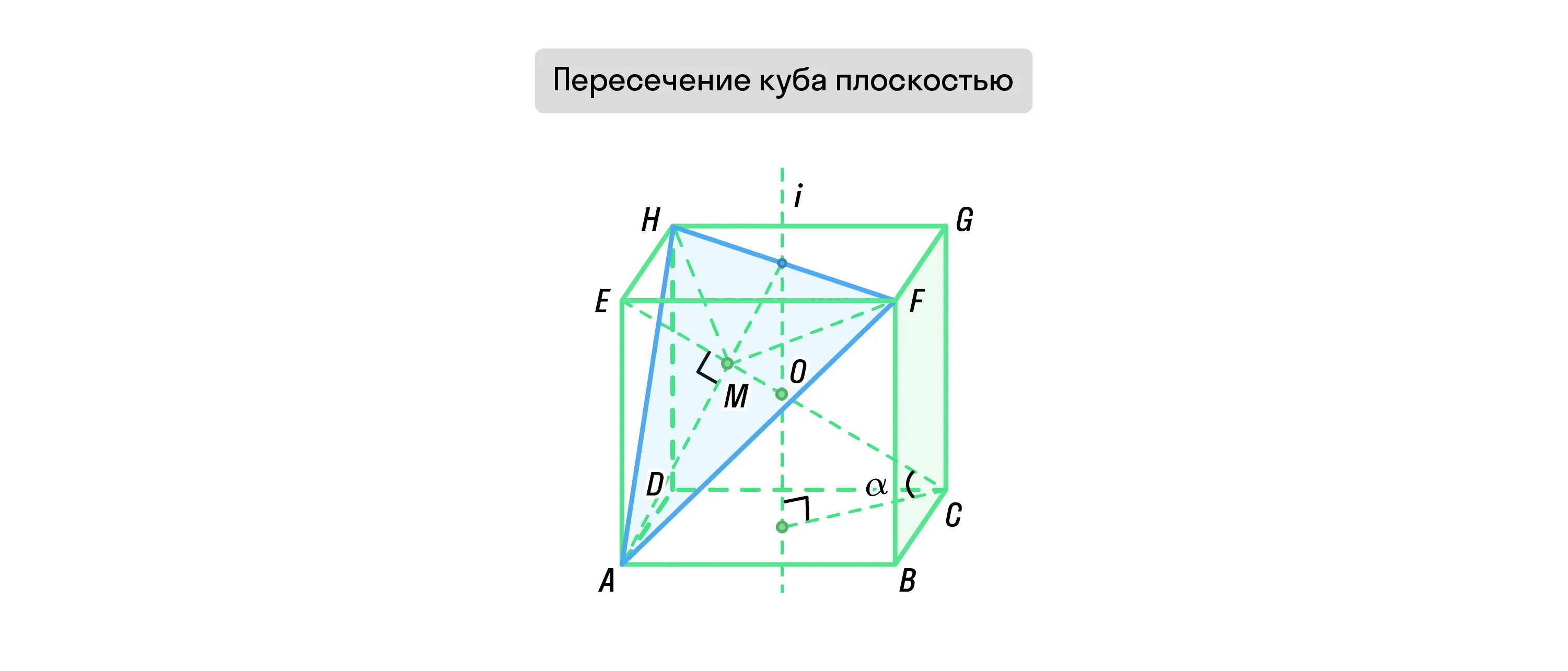
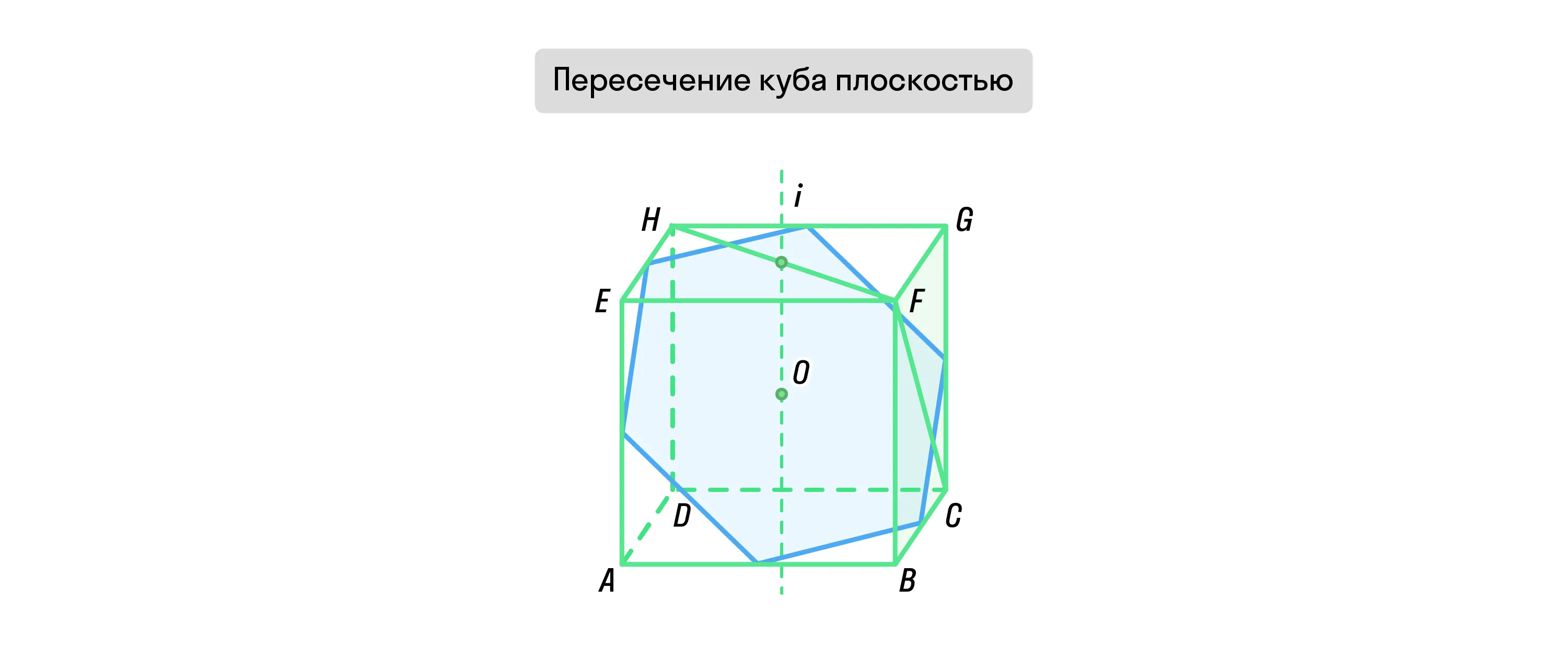
Если куб пересекает плоскость, которая проходит через его центр и середины 6 граней, то в сечении будет правильный шестиугольник. Сторона такого шестиугольника будет равна a√2/2, а площадь сечения — a²(3√3)/4.

В этом случае одна из диагоналей каждой грани куба, что пересекаются, будет перпендикулярна стороне шестиугольника.

Все формулы для решения задач с кубом

Куб: все формулы
Диагональ куба через длину ребра
Диагональ грани через длину ребра
Объём куба через длину ребра
Объём куба через длину диагонали
Площадь поверхности куба через длину ребра
Периметр куба через длину ребра
Радиус вписанной сферы через длину ребра
Объём вписанной сферы через длину ребра
Радиус описанной сферы через длину ребра
Объём сферы, описанной вокруг куба, через длину ребра

Убедитесь, что вы готовы к заданиям по стереометрии, — проверьте свои силы на Тренажёре ЕГЭ. В нём 24/7 доступны экзаменационные задачи с кубами и на другие темы. Причём можно выбрать для практики как один тип заданий, так и написать пробный экзамен целиком. Это бесплатно!