Объём параллелепипеда — это величина, показывающая, сколько пространства занимает данное тело. Вычисляется по формуле:
Например, для параллелепипеда с длиной 3 м, шириной 2 м и высотой 4 м, объём = 3 м × 2 м × 4 м = 24 м³.
Для кого эта статья:
- школьники и студенты, изучающие геометрию и объемные фигуры
- Учителя и преподаватели математики, ищущие объясняющие материалы для своих учащихся
- Любой желающий узнать о вычислении объема параллелепипеда и связанных с ним задачах
Понятие объема
Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.
Объём — это количественная характеристика пространства, занимаемого телом или веществом.
Другими словами, это то, сколько места занимает предмет.
Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.
За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см3), кубический миллиметр (1 мм3), кубический метр (1 м3).
Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.
|
Два свойства объёма
|
Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.
Объем прямоугольного параллелепипеда
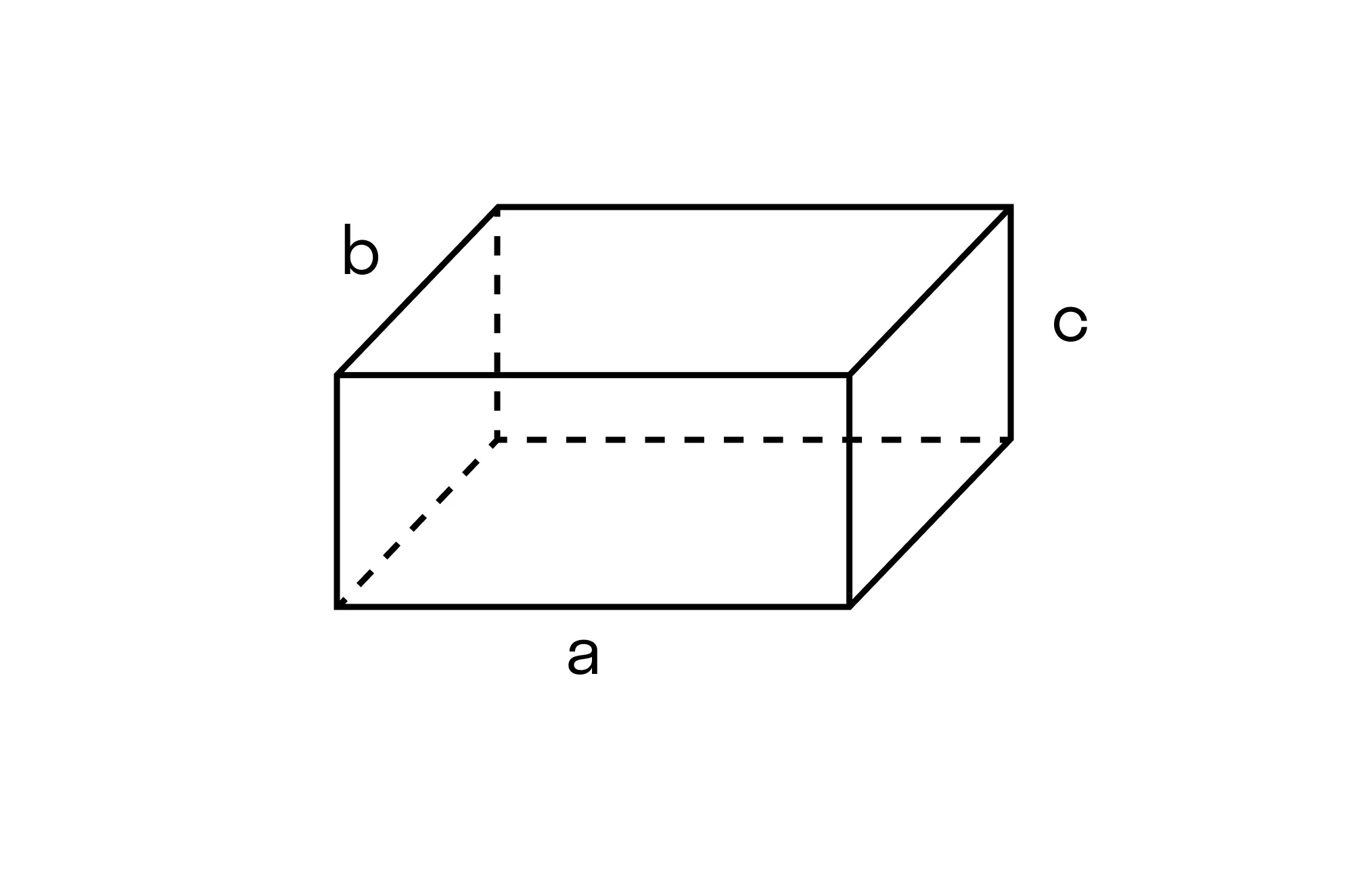
Объём прямоугольного параллелепипеда можно найти, умножив его длину (a), ширину (b) и высоту (h).
Формула для расчёта объёма: V = a * b * h, где V — объём, a, b и h — соответствующие стороны параллелепипеда.
Пример:
- если a = 2 м,
- b = 3 м,
- h = 4 м,
- то V = 2 * 3 * 4 = 24 м³.
Параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.
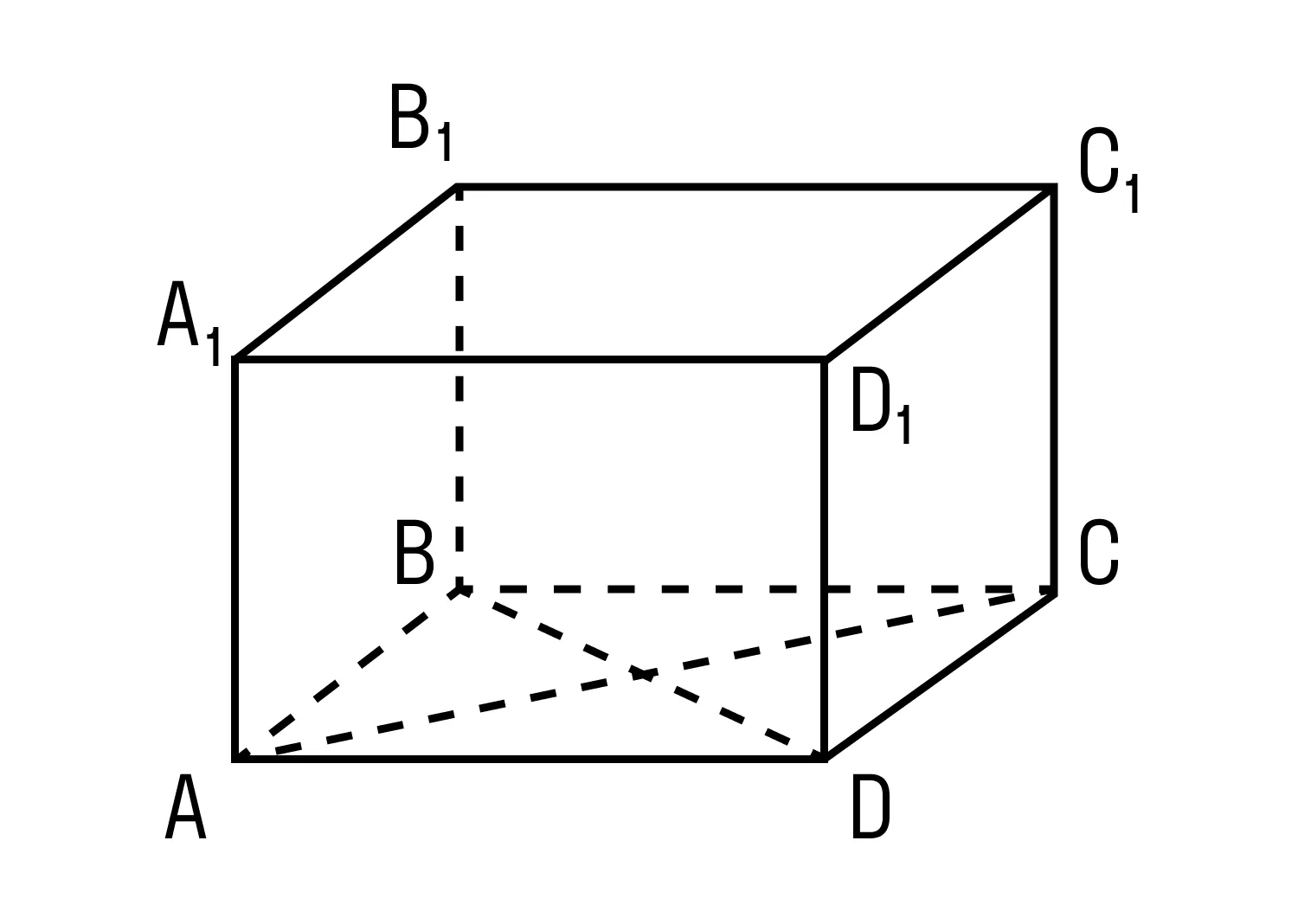
Прямоугольным параллелепипедом называют параллелепипед, у которого все грани являются прямоугольниками.
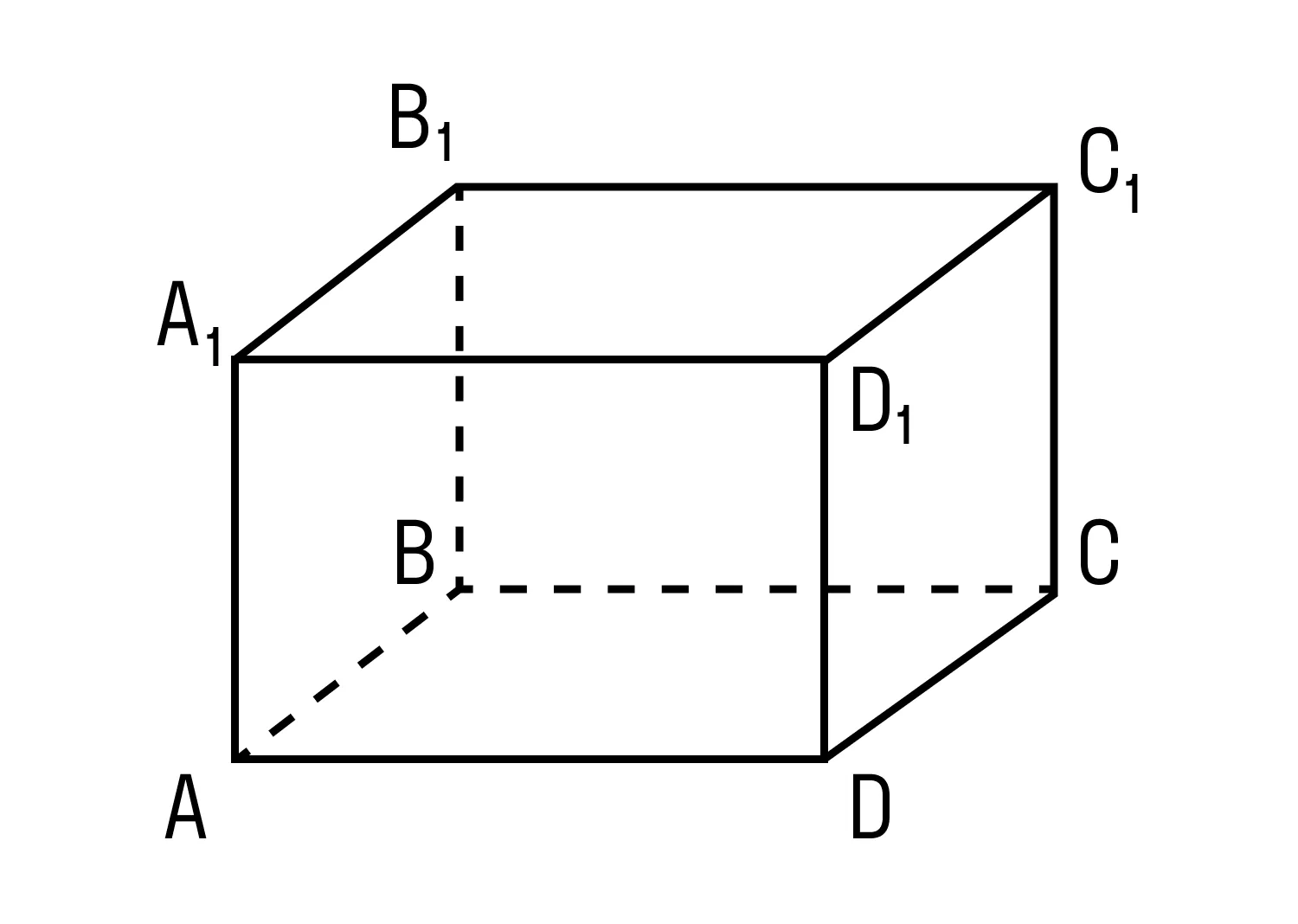
|
Формула объема прямоугольного параллелепипеда Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты: V = a × b × h |
Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.
|
a |
длина параллелепипеда |
|
b |
ширина параллелепипеда |
|
h |
высота параллелепипеда |
|
P (осн) |
периметр основания |
|
S (осн) |
площадь основания |
|
S (бок) |
площадь боковой поверхности |
|
S (п.п.) |
площадь полной поверхности |
|
V |
объем |
Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.
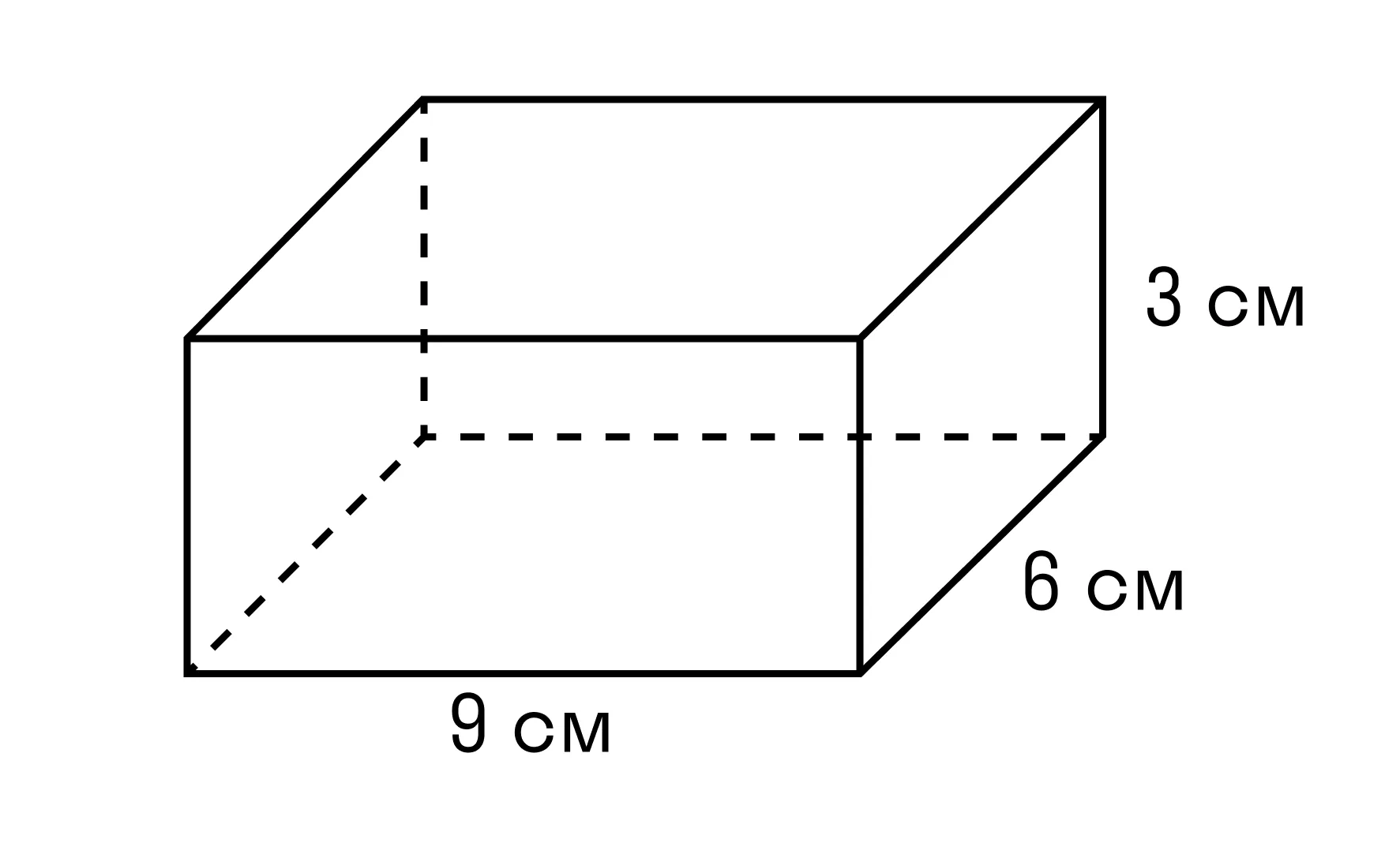
a = 9 см
b = 6 см
h = 3 см
V = a × b × h
V = 9 × 6 × 3 = 162 см3.
Ответ: объем прямоугольного параллелепипеда равен 162 см3.
|
Следствие Объем параллелепипеда равен произведению площади основания на высоту. V = Sосн × h |
Из этого следствия выведем формулу нахождения площади основания параллелепипеда.
Sосн = V : h
Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 96 см3, а высота 8 см.
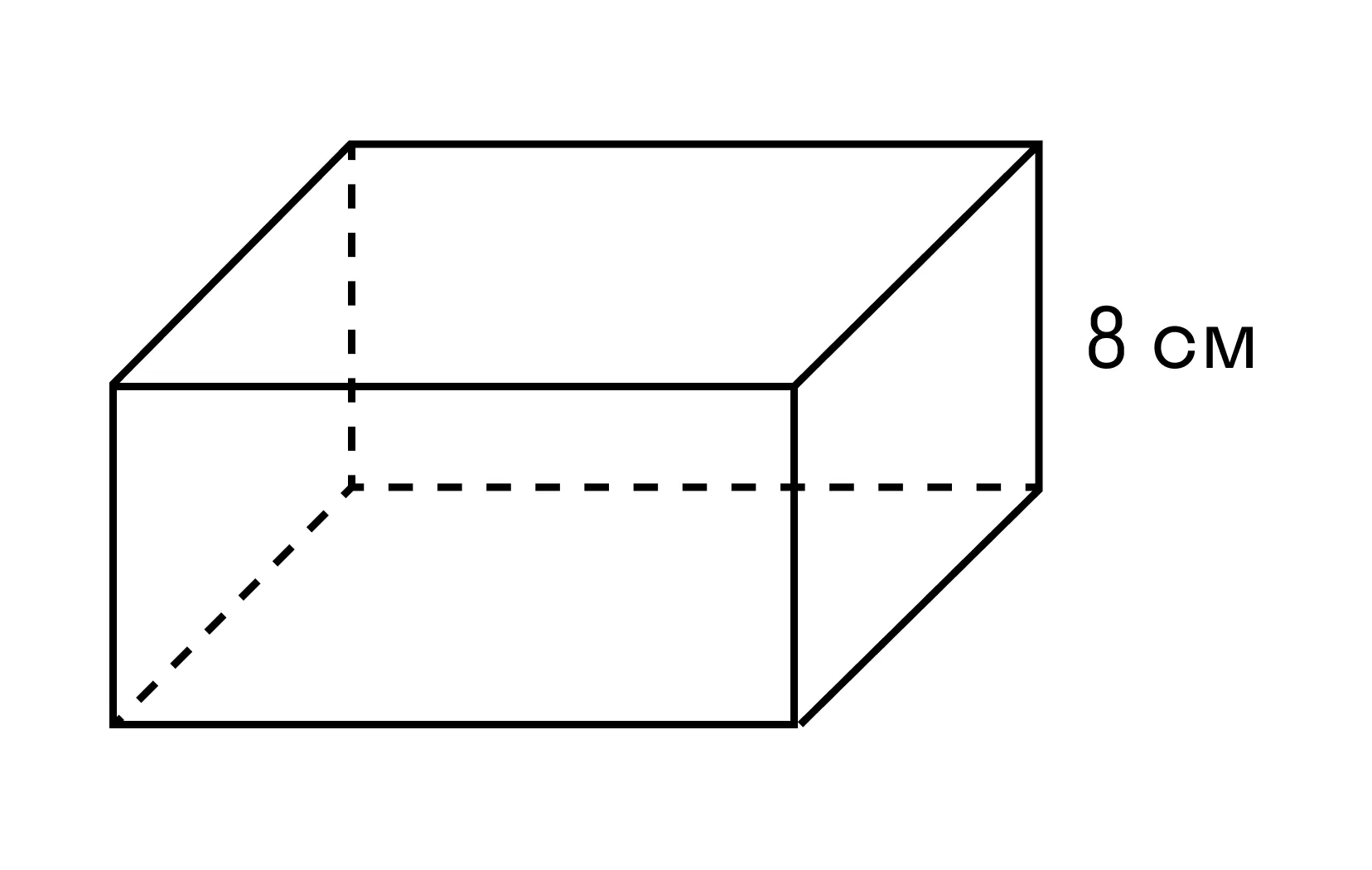
V = 96 см3
h = 8 см
V = Sосн × h
Sосн = V : h
Sосн = 82 см3 : 8 см = 12 см2.
Ответ: площадь основания параллелепипеда равна 12 см2.
Обучение на курсах по математике в онлайн-школе Skysmart поможет быстрее разобраться в теме и правильно решать задачки!
Получи больше пользы от Skysmart:
-
Прокачивай знания на курсах математики
-
Выбирай из 1200+ репетиторов по математике
Записывайся на бесплатные курсы для детей
Вычисление площади
Площадь параллелепипеда - это сумма площадей всех его шести граней. Формула для вычисления общей площади параллелепипеда: S = 2(ab + bc + ac), где a, b, c – длины ребер параллелепипеда.
Примеры:
- Для параллелепипеда со сторонами 2, 3 и 4: S = 2(2*3 + 3*4 + 2*4) = 2(6 + 12 + 8) = 52
- Для куба со стороной a: S = 6a².
Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде.
Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений.
Так как противолежащие грани прямоугольного параллелепипеда одинаковые, то получим формулу:
- Sб. п. = 2 (ac + bc)
Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания. Так как площади оснований у прямоугольного параллелепипеда одинаковые, то получим формулу:
- Sп. п. = 2 (ab + ac + bc)
Пример 3. Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (6 × 4 + 6 × 3 + 4 × 3) = 2 × (24 + 18 + 12) = 2 × 54 = 108 см2.
Ответ: площадь поверхности параллелепипеда — 108 см2.
Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно.
Задачи на самопроверку
Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.
Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.
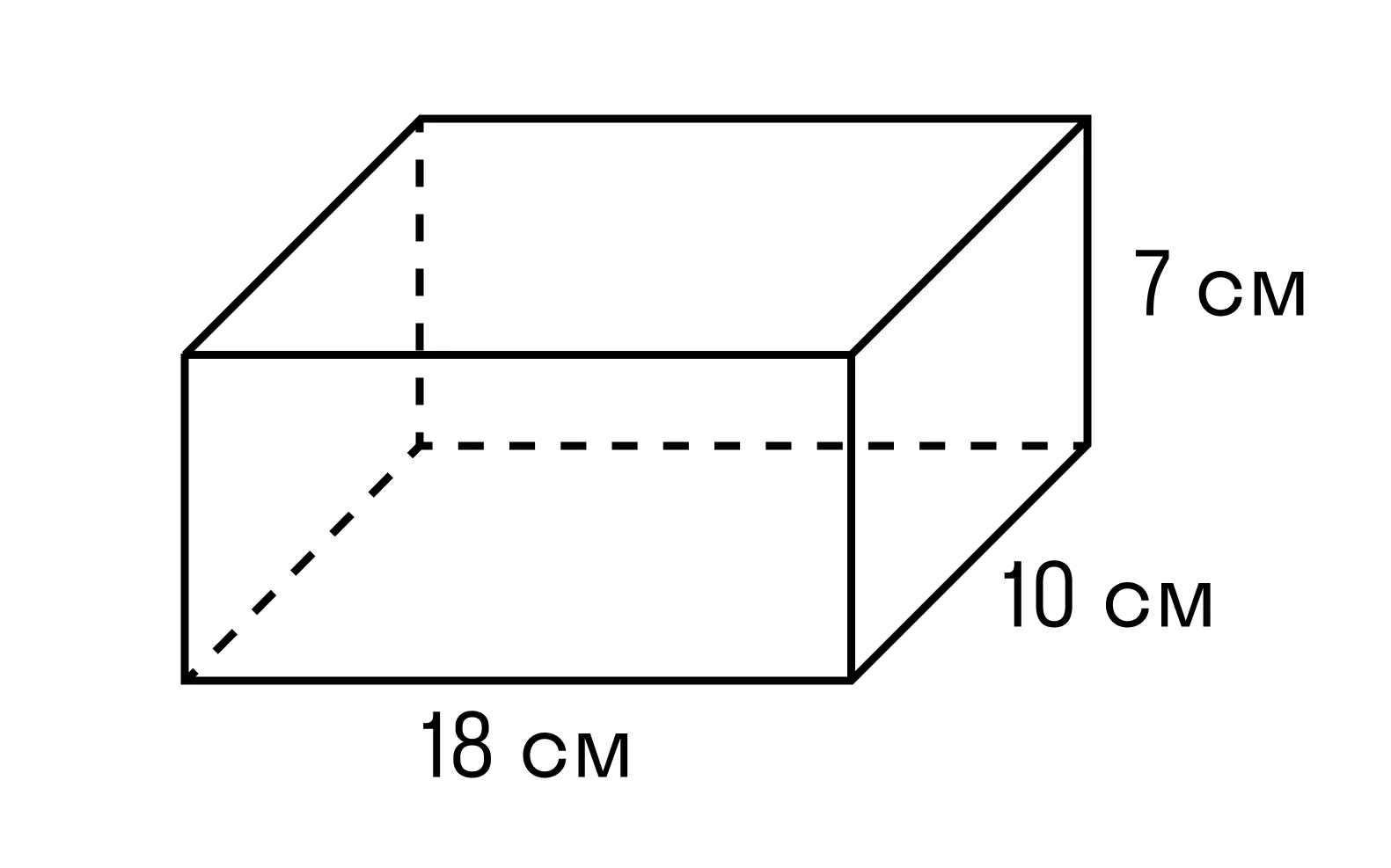
Как решаем:
a = 18 см
b = 10 см
h = 7 см
Формула нахождения объема параллелепипеда:
V = a × b × h
Подставляем наши числа:
V = 18 × 10 × 7 = 1260 см3.
Ответ: объём параллелепипеда равен 1260 см3.
Задачка 2. Найдите площадь основания параллелепипеда, если его объём равен 120 см3, а высота — 15 см.
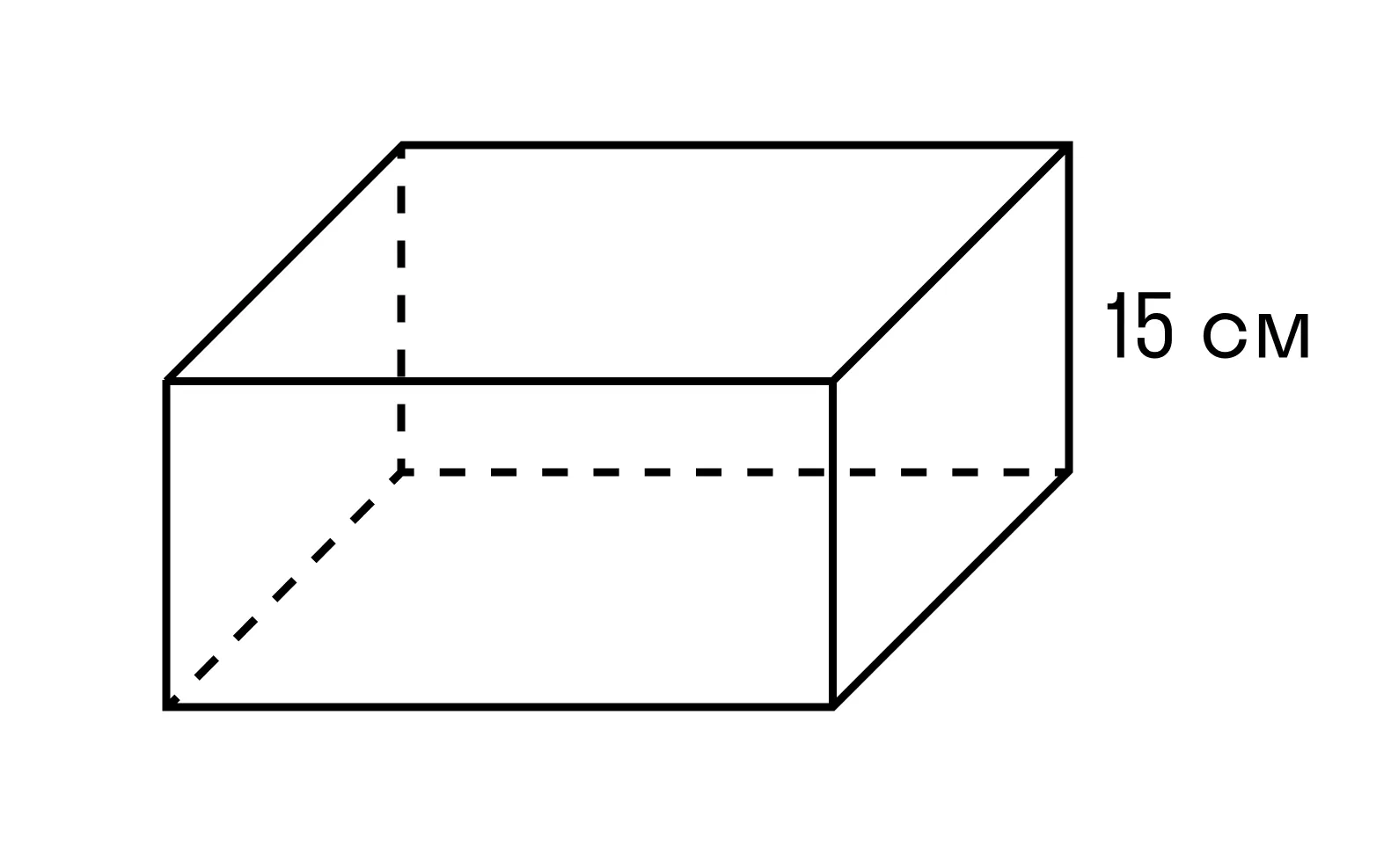
Как решаем:
V = 120 см
h = 15 см
V = Sосн × h
Sосн = V : h
Sосн = 120 см3: 15 см = 8 см2.
Ответ: площадь основания параллелепипеда равна 8 см2.
Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания равна 30 сантиметров, ширина равна 12 см, а высота равна 5 см.
Как решаем:
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (30 × 12 + 30 × 5 + 12 × 5) = 2 × (360 + 150 + 60) = 2 × 570 = 1140 см2.
Ответ: площадь полной поверхности параллелепипеда равна 1140 см2.
Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.
|
V параллелепипеда |
V = a × b × h |
|
|
V = Sосн × h |
|
S боковой поверхности |
Sб. п. = 2 (ac + bc) |
|
S полной поверхности |
Sп. п. = 2 (ab + ac + bc) |