Многогранники и их свойства
Многогранник — это геометрическое тело, которое ограничено конечным числом плоских многоугольников.
Такие многоугольники — это грани многогранника. Также у него есть рёбра — стороны граней, вершины — точки, где рёбра пересекаются друг с другом, и диагональ — отрезок, соединяющий две вершины, не принадлежащие одной грани.
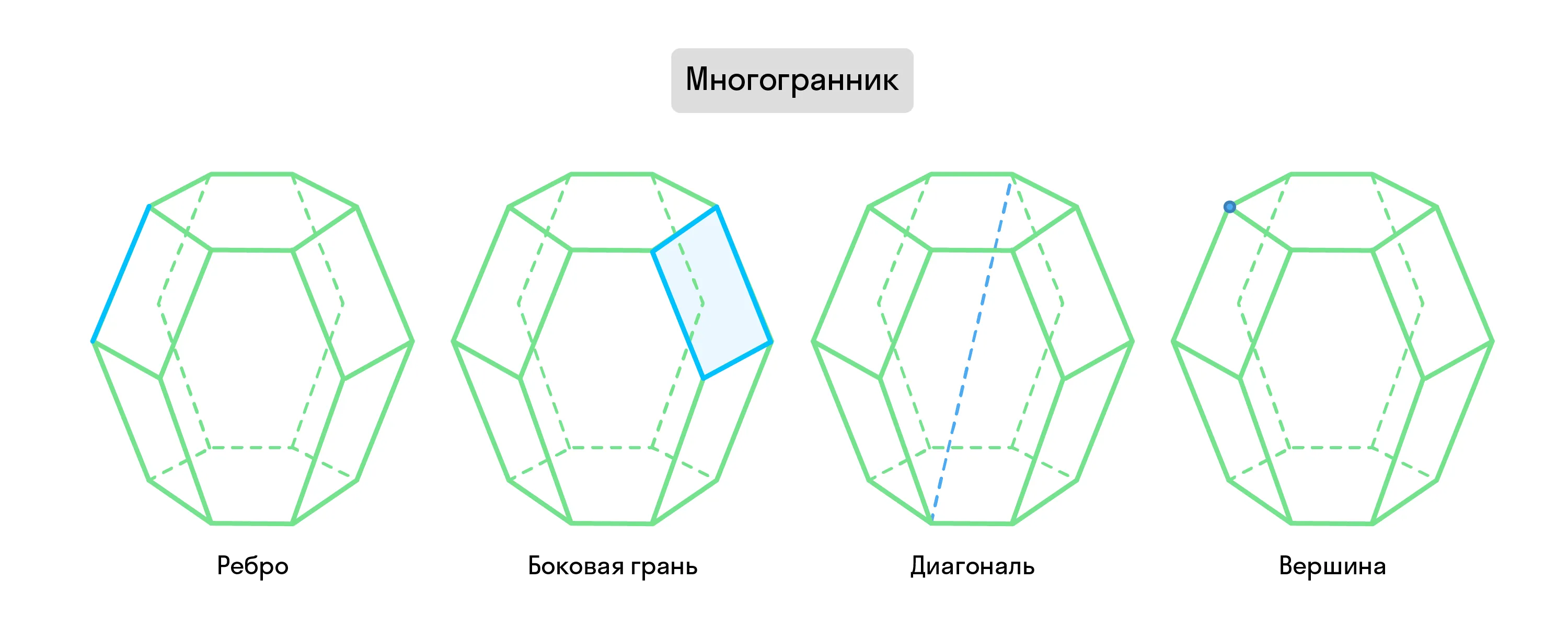
Как и многоугольники, многогранники бывают выпуклыми и невыпуклыми (вогнутыми).
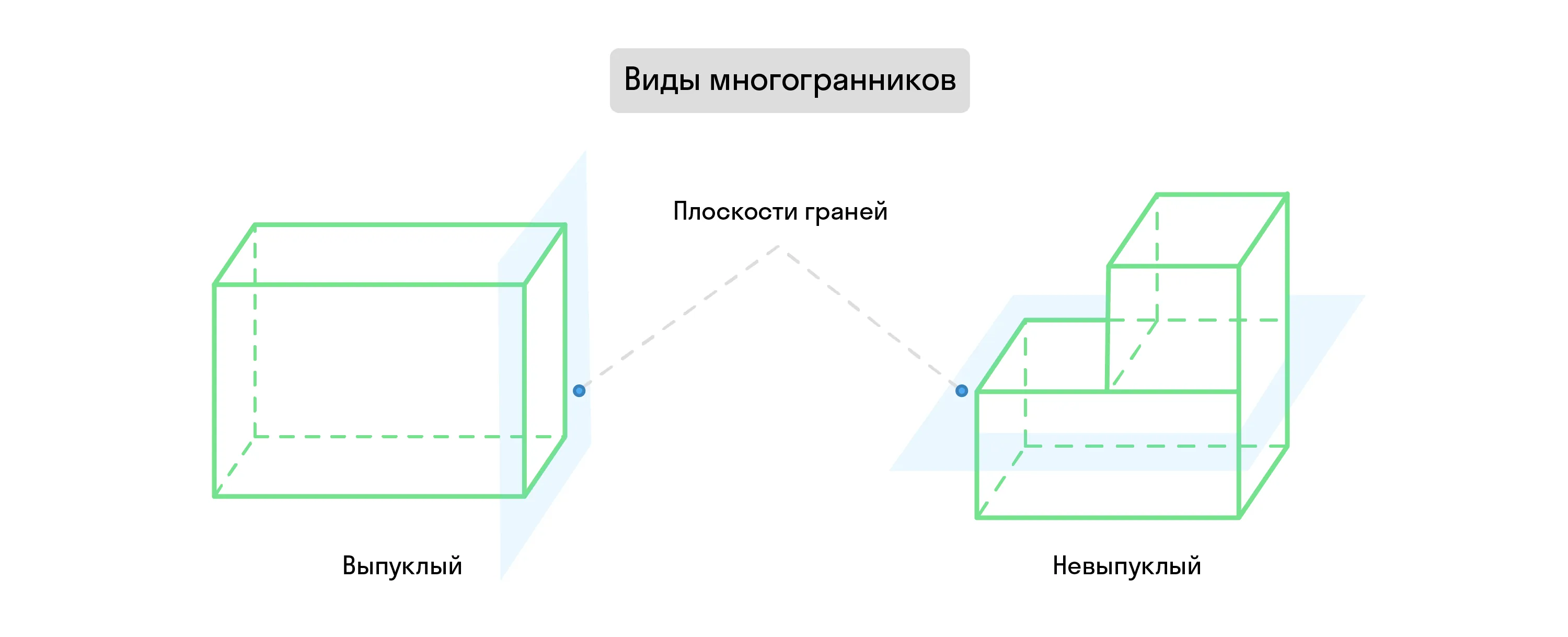
Выпуклый многогранник — это такой многогранник, который целиком расположен по одну сторону от плоскости одной из своих граней.
Все грани такого многогранника — это выпуклые многоугольники. Т. е. фигуры, которые лежат по одну из сторон своих граней.
Невыпуклый (вогнутый) многогранник — это такой многогранник, плоскости граней которого делят его на части.
На рисунке ниже видно, как плоскость проходит через многогранник и делит его на верхний и нижний сегменты.
Правильные многогранники
Правильный многогранник — это выпуклый многогранник, грани которого — правильные многоугольники. При этом в каждой его вершине сходится одинаковое количество рёбер.
Т. о., все рёбра правильного многогранника равны между собой. То же самое справедливо и для двугранных углов, которые включают грани с общим ребром.
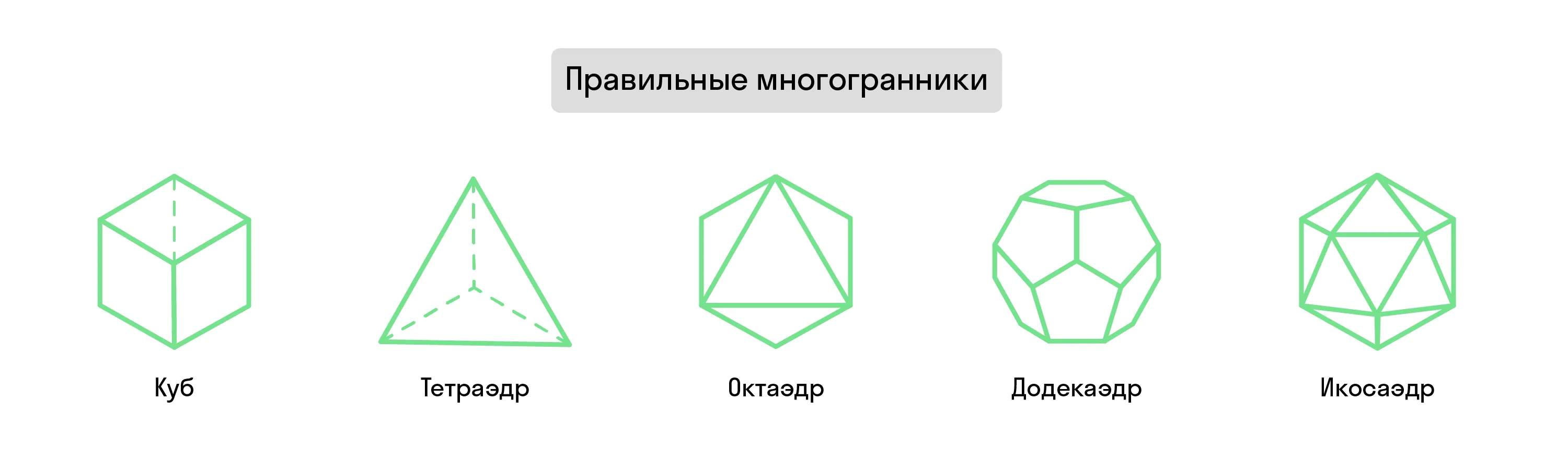
Всего есть пять видов правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр.
Теорема Эйлера
С вопросом, какими бывают правильные многогранники, в своё время помогла разобраться теорема Эйлера
Теорема Эйлера для многогранников
В любом выпуклом многограннике сумма числа граней и числа вершин на 2 больше числа рёбер.
Если представить число рёбер как
Теперь подставим в неё значения для каждого элемента существующих правильных многогранников и получим:
-
тетраэдр: 4 – 6 + 4 = 2;
-
куб: 8 – 12 + 6 = 2;
-
октаэдр: 6 – 12 + 8 = 2;
-
икосаэдр: 12 – 30 + 20 = 2;
-
додекаэдр: 20 – 30 + 12 = 2.
В каждом случае сохраняется соотношение сторон, вершин и граней по теореме Эйлера.
Не бывает правильных многогранников, гранями которых были бы правильные многоугольники с 6 и более сторонами. Есть и минимальное число сторон таких граней — 4.
Выходит,
Получи больше пользы от Skysmart:
-
Подготовься к ОГЭ на пятёрку.
-
Подготовься к ЕГЭ на высокие баллы.
Записывайся на бесплатные курсы для детей.
Решай задания в бесплатном тренажёре ЕГЭ.
Призма и её свойства
Призма — это выпуклый многогранник, две грани которого представляют собой равные многоугольники, расположенные в параллельных плоскостях. При этом все рёбра, не лежащие в этих плоскостях, параллельны между собой.
Эти два равных многоугольника — основания призмы. Остальные её стороны, которые представляют собой параллелограммы, называют боковыми гранями. Эти элементы определяют вид призмы.
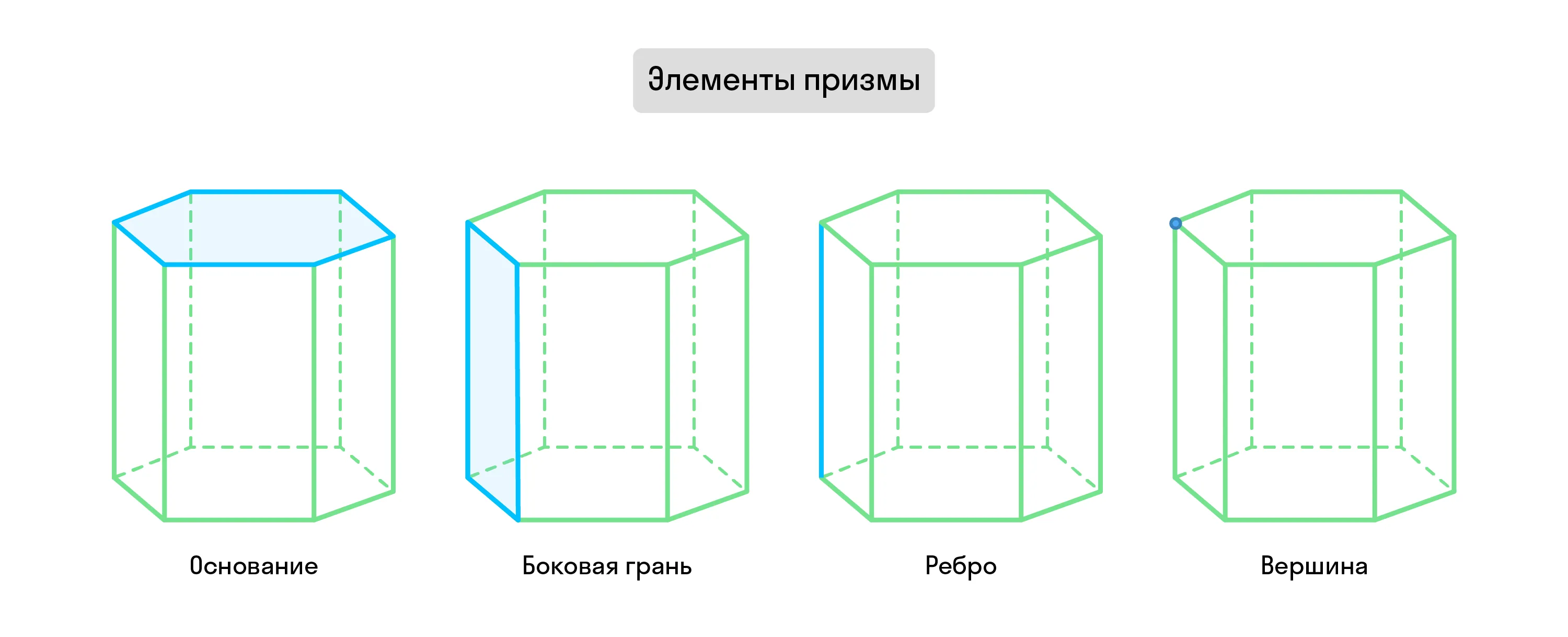
Призму с основаниями-треугольниками называют треугольной. По этому же принципу существуют четырёхугольные, пятиугольные и любые другие n-угольные призмы.
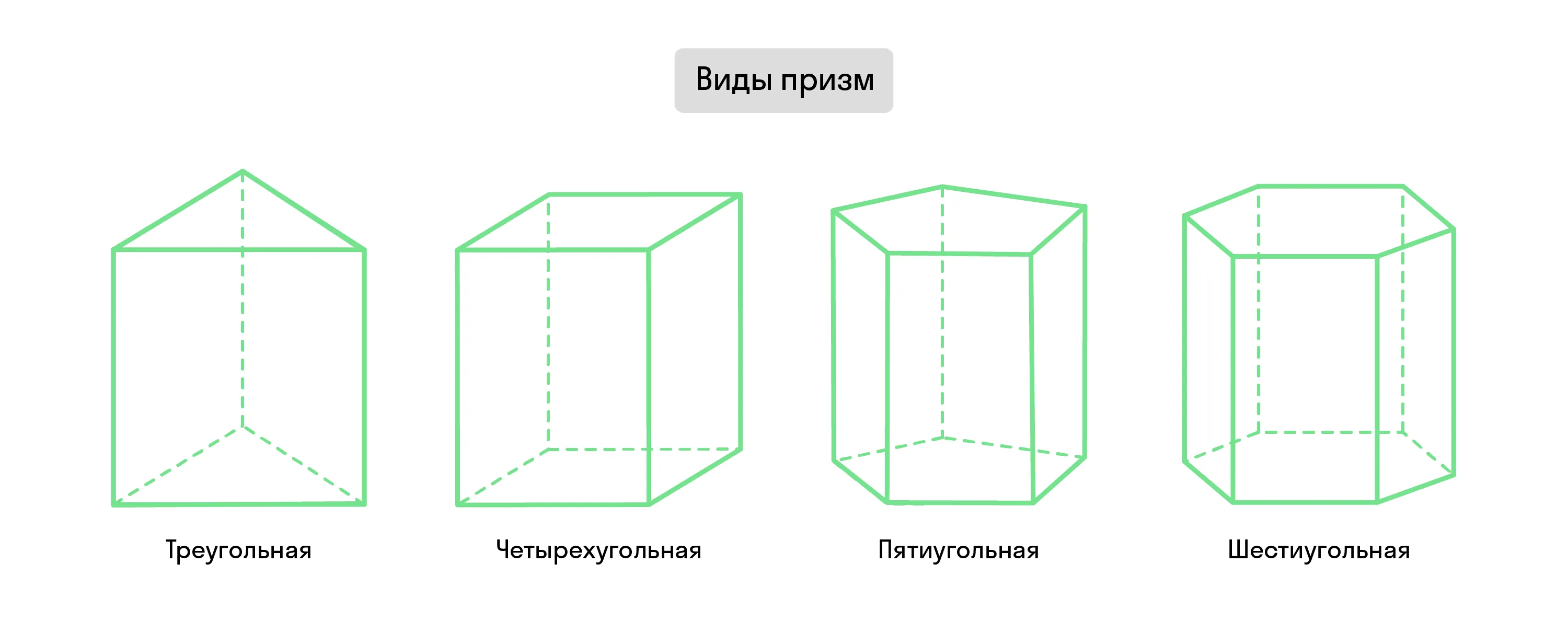
Призму, боковые рёбра которой перпендикулярны плоскости основания, называют прямой. Все остальные призмы, не подходящие под это определение, — наклонные.
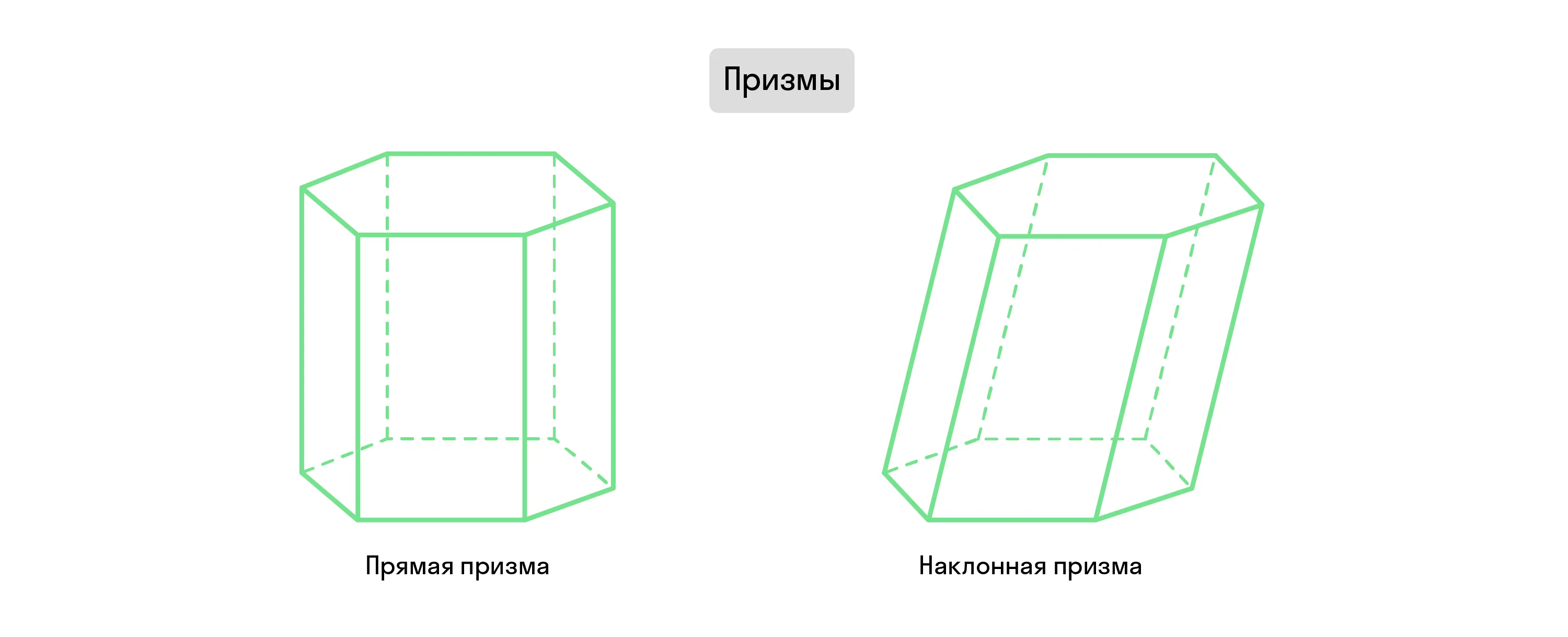
Если из любой точки одного основания провести перпендикулярную прямую к плоскости другого, такая прямая будет считаться высотой призмы.
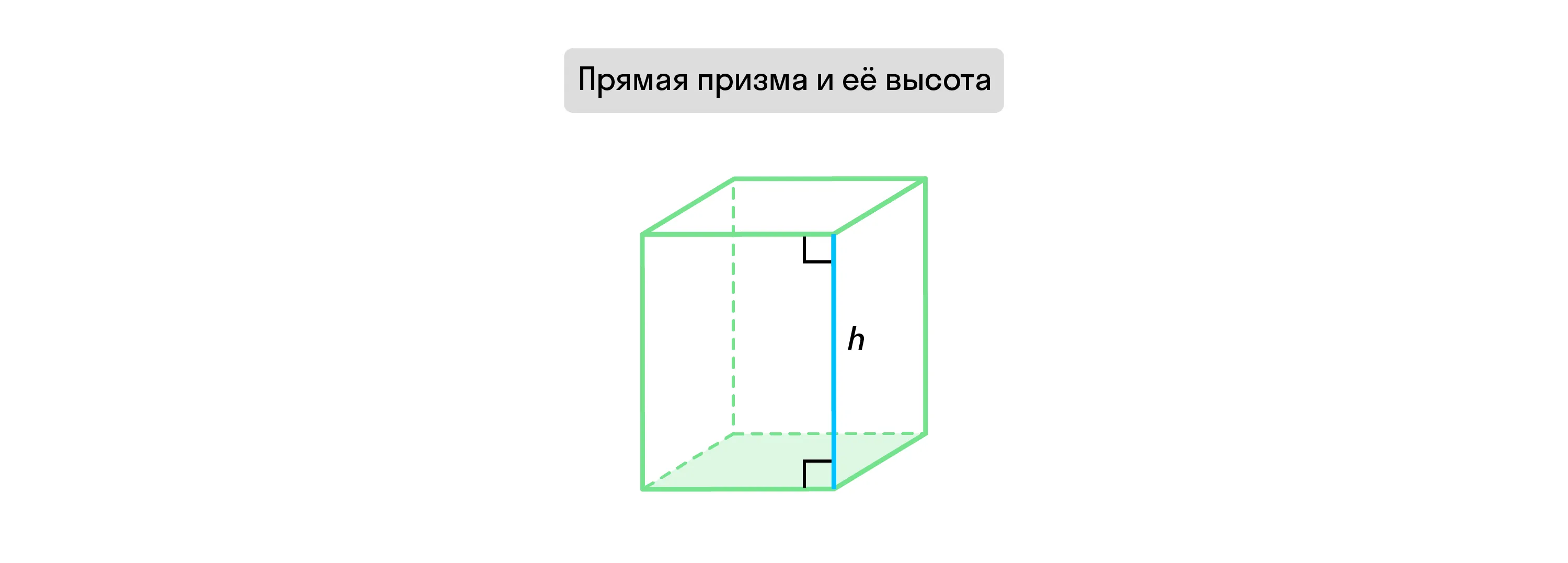
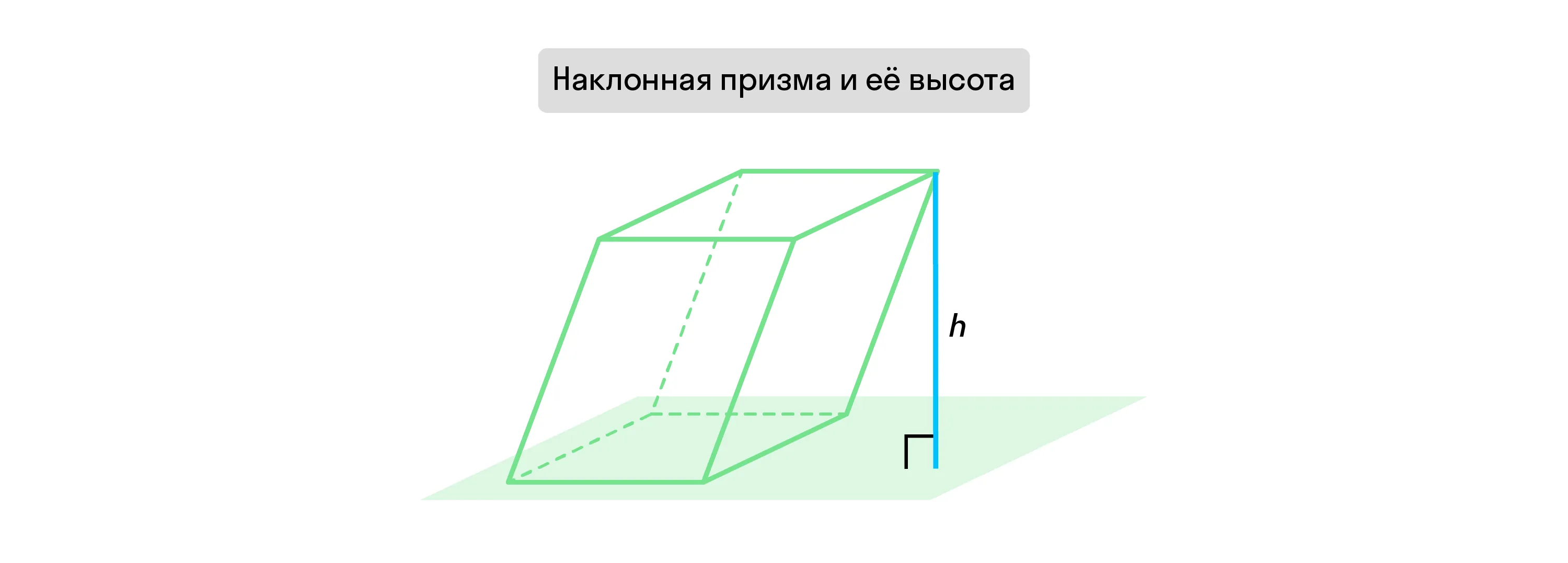
Призма называется правильной, если её основания — это правильные многоугольники.
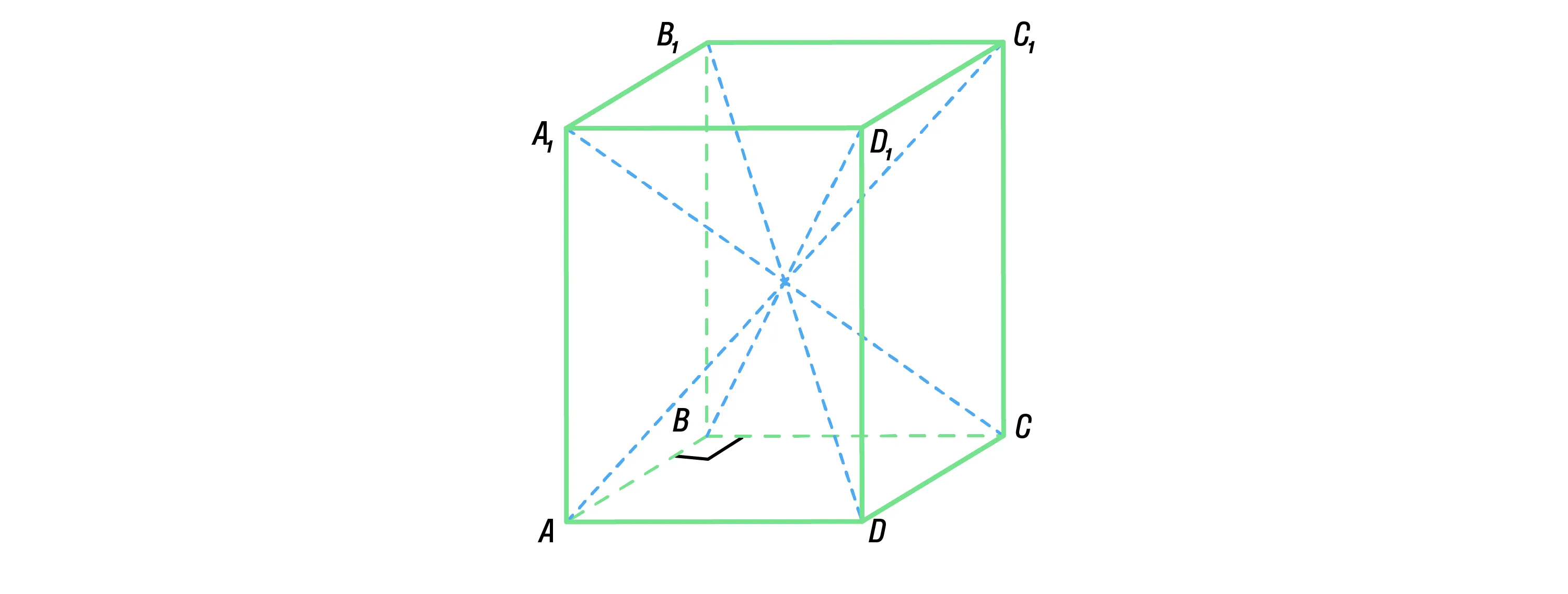
Важное свойство правильной призмы заключается в том, что все её диагонали равны. Также они всегда пересекаются в одной точке, которая делит их пополам.
|
Призма: все формулы |
|
|---|---|
|
Объём призмы через площадь основания и высоту |
|
|
Объём наклонной призмы через площадь перпендикулярного сечения и длину бокового ребра |
|
|
Объём правильной прямой призмы через высоту ( |
|
|
Площадь боковой поверхности призмы через периметр основания и высоту |
|
|
Площадь поверхности призмы через площадь основания, периметр основания и высоту |
|
|
Площадь поверхности правильной призмы через высоту ( |
|
Параллелепипед и его свойства
Параллелепипед — это четырёхугольная призма, основания которой — параллелограммы.
Противоположные грани такой фигуры равны и параллельны друг другу, а значит, она также считается правильной. При этом, если основания параллелепипеда — это прямоугольники, его так и называют — прямоугольный.
Все прямоугольные параллелепипеды — прямые, т. к. их боковые грани находятся под углом 90° относительно основания. Если грани не перпендикулярны основаниям, параллелепипед считается наклонным.
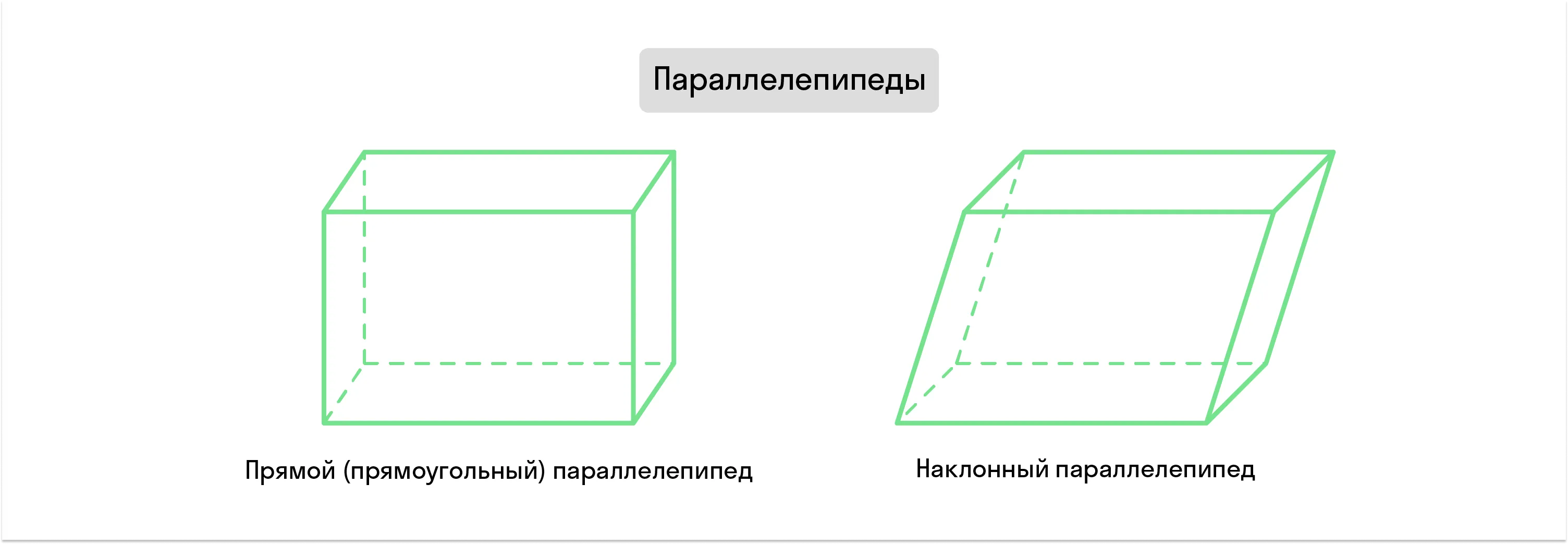
Все 4 диагонали прямоугольного параллелепипеда равны и пересекаются в одной точке. Длина его диагонали и длины попарно перпендикулярных рёбер
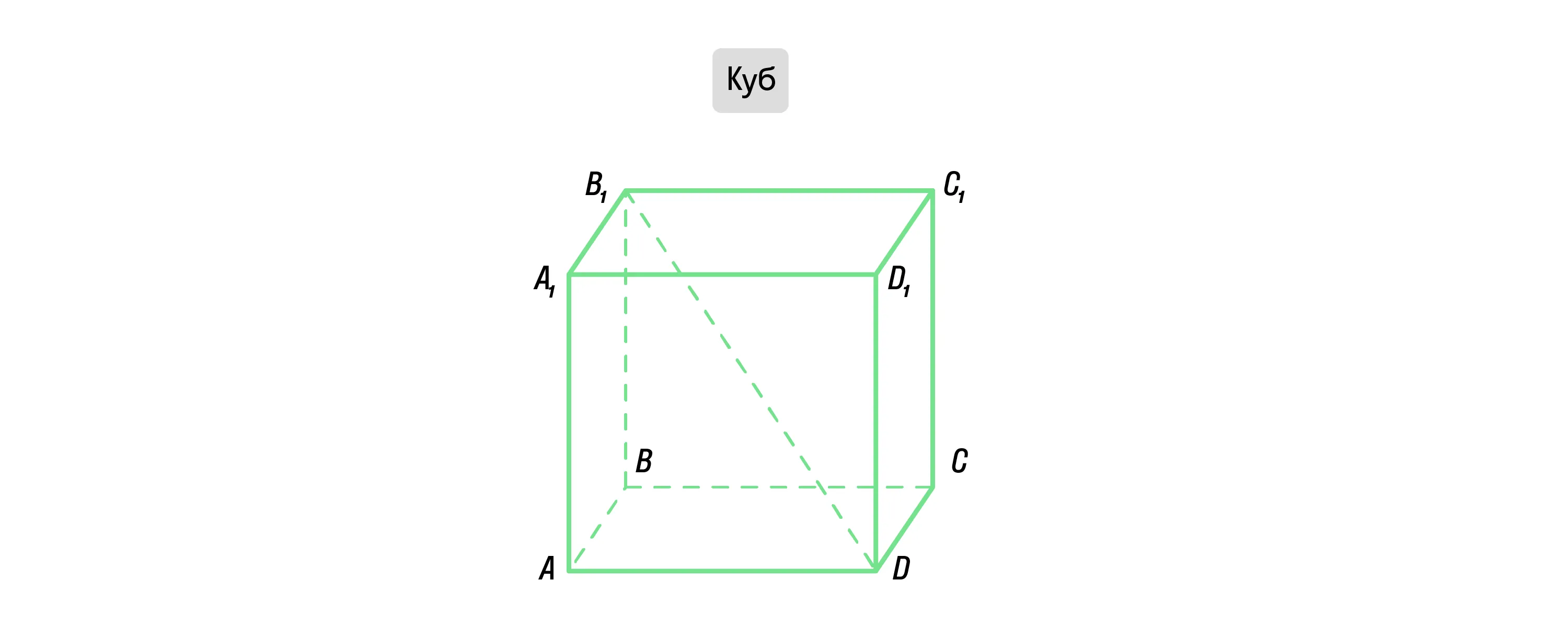
Прямой параллелепипед, основания которого — это квадраты, называют кубом.
Куб — правильная фигура. Все его рёбра равны между собой, а также боковые грани равны основаниям. Иначе говоря, куб целиком состоит из 6 квадратов.
|
Параллелепипед: все формулы |
|
|---|---|
|
|
|
|
Площадь поверхности прямоугольного параллелепипеда через длины его сторон |
|
|
Длина диагонали прямоугольного параллелепипеда через длины его сторон |
|
|
Диагональ куба через длину ребра ( |
|
|
Диагональ грани через длину ребра ( |
|
|
Объём куба через длину ребра ( |
|
|
Объём куба через длину диагонали |
|
|
Площадь поверхности куба через длину ребра ( |
|
|
Периметр куба через длину ребра ( |
|
|
Радиус вписанной сферы через длину ребра ( |
|
|
Объём вписанной сферы через длину ребра ( |
|
|
Радиус описанной сферы через длину ребра ( |
|
|
Объём сферы, описанной вокруг куба, через длину ребра ( |
|
Пирамида и её свойства
Пирамида — это многогранник, который состоит из многоугольника в основании и треугольников, образованных при соединении точки вершины пирамиды и вершин её основания.
Треугольники — это боковые грани пирамиды, а её ребра — это общие стороны треугольников. Также у пирамиды есть апофема — перпендикулярная прямая, опущенная из её вершины к стороне основания.
Пирамида может быть остроугольной и тупоугольной. В первом случае апофема больше длины стороны основания, во втором — меньше.
Если высота пирамиды соединяет её вершину с центром основания, а оно само представляет из себя правильный многоугольник, то и пирамида называется правильной.
Все боковые грани такой фигуры — одинаковые равнобедренные треугольники.
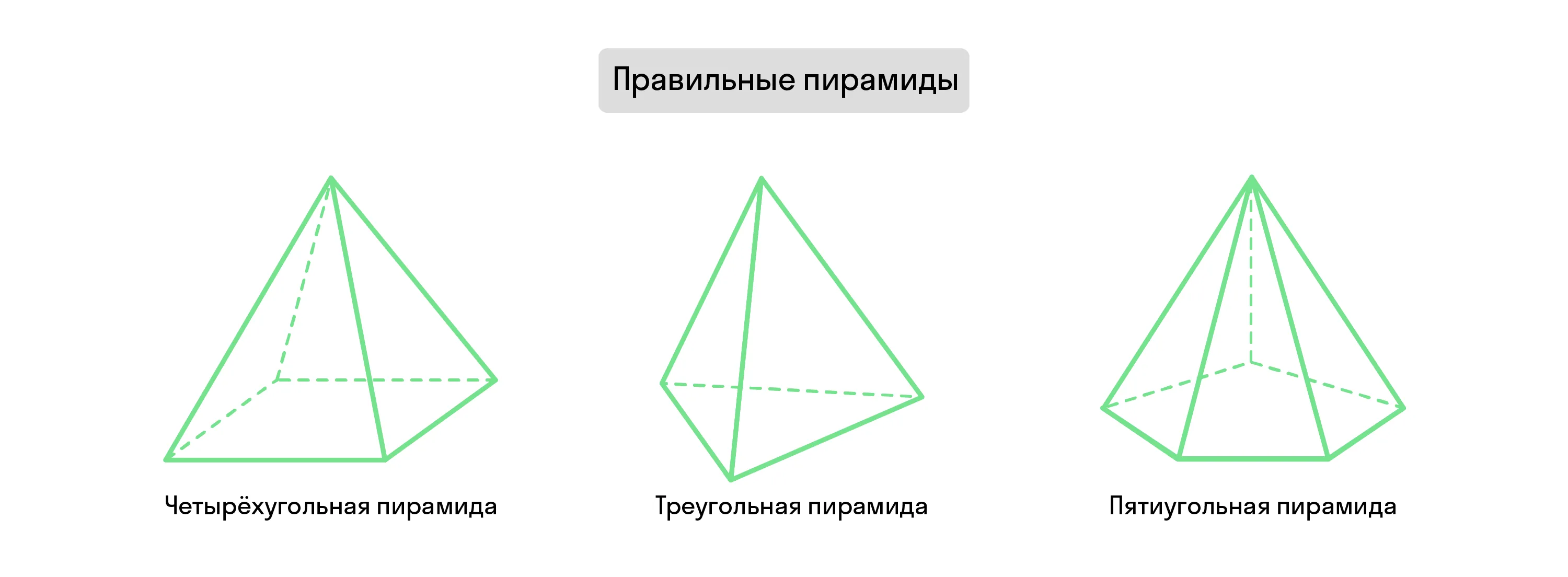
В этом случае все рёбра пирамиды наклонены к её основанию под одинаковыми углами.
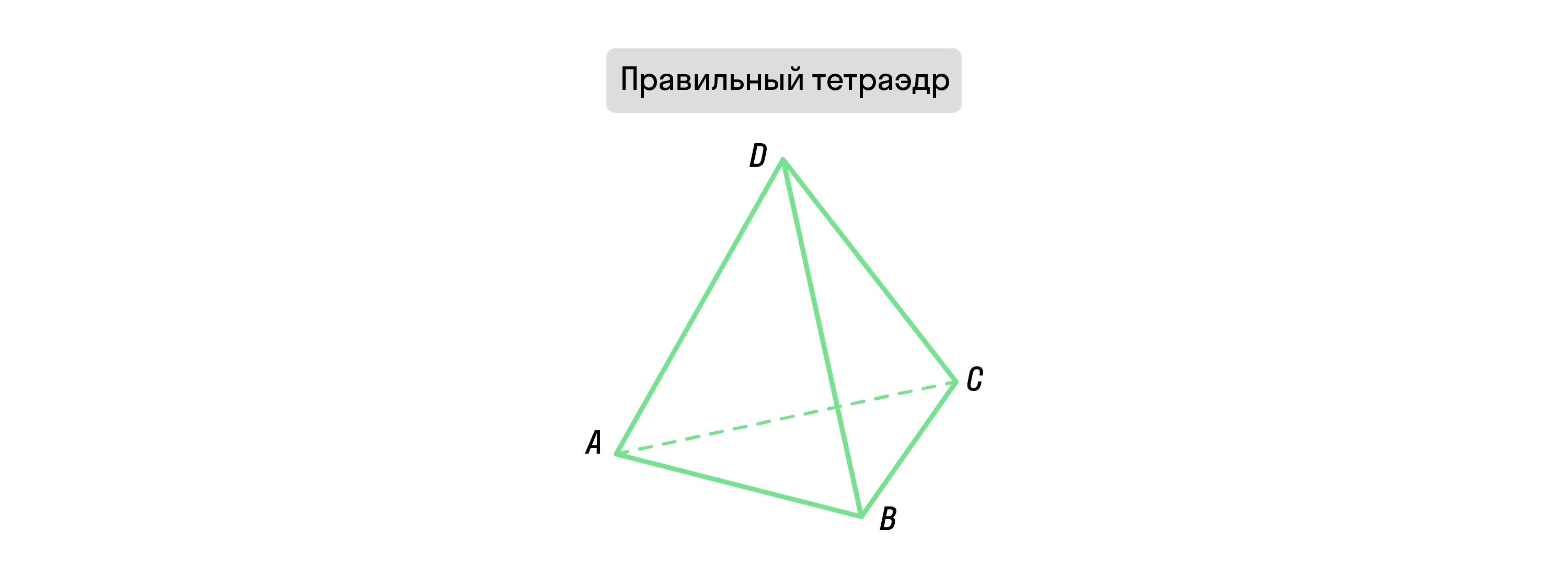
Если все грани правильной пирамиды — это равносторонние треугольники, то она называется правильным тетраэдром.
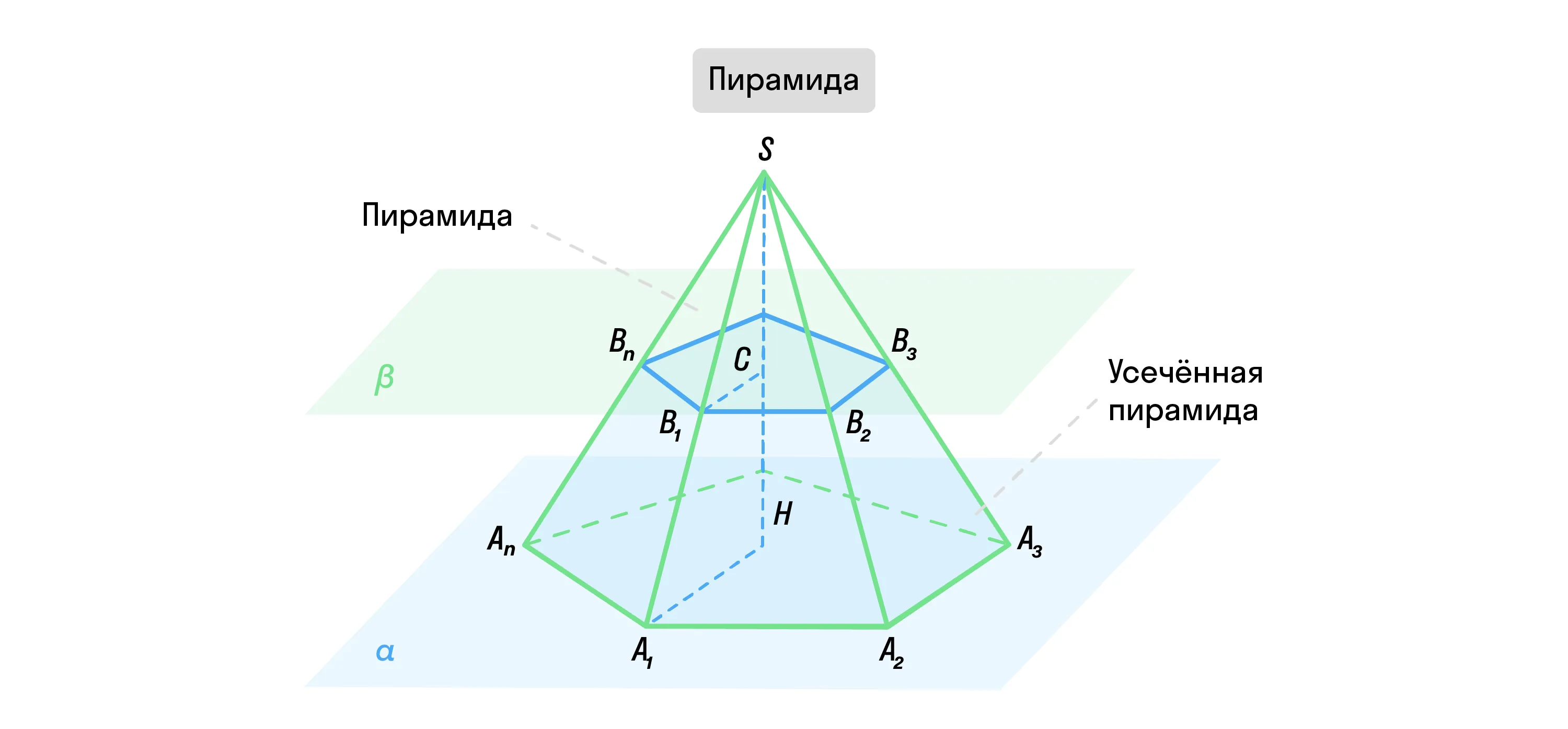
Если пирамиду разделяет плоскость, параллельная основанию фигуры, её нижняя часть называется усечённой пирамидой.
Параллельные грани такой пирамиды считают её основаниями. Расстояние между ними, т. е. перпендикуляр, опущенный от одного основания к другому, — высота усечённой пирамиды.
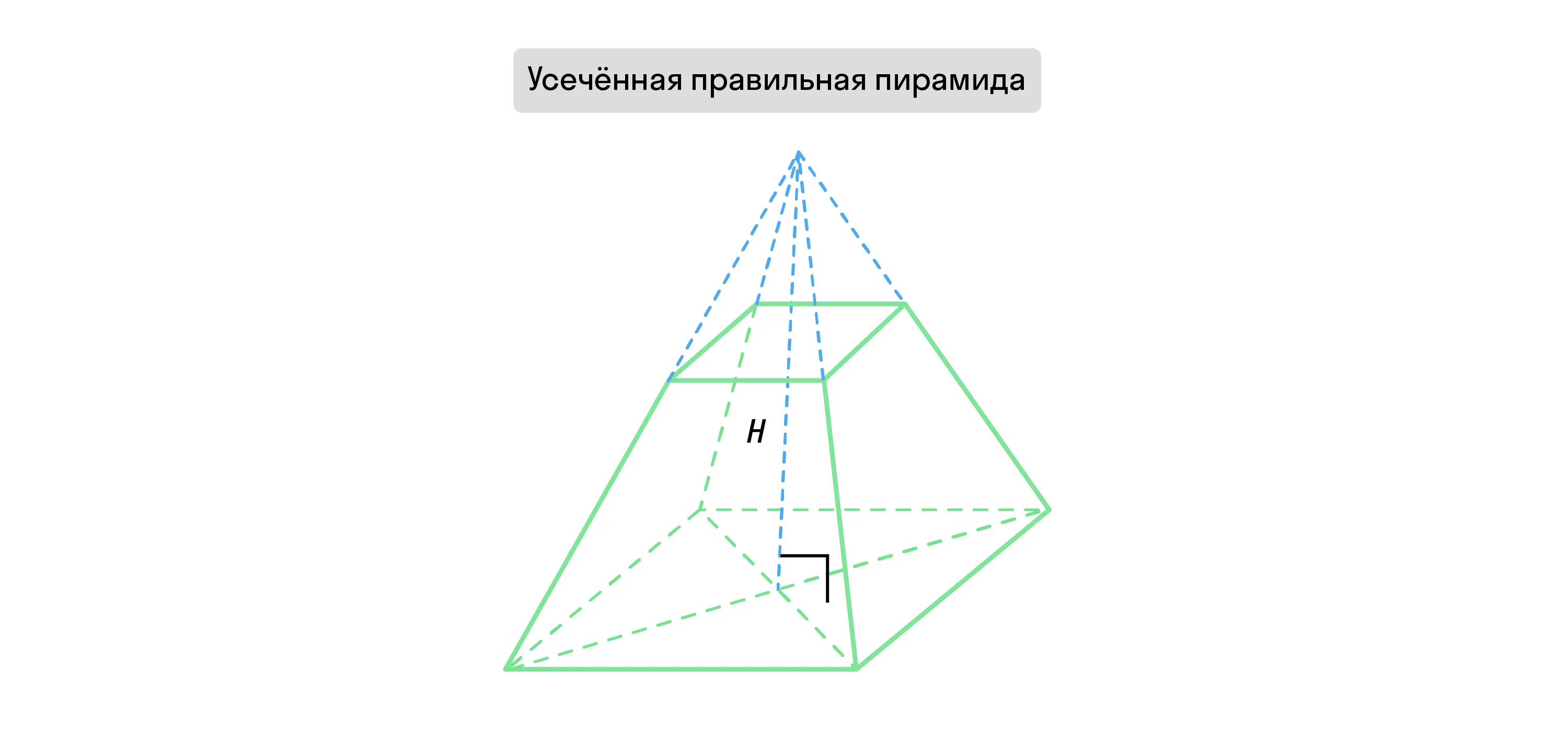
Если такая фигура была получена усечением правильной пирамиды, её называют усечённой правильной пирамидой.
|
Пирамида: все формулы |
|
|---|---|
|
Объём пирамиды через площадь основания и высоту |
|
|
Площадь боковой поверхности правильной пирамиды через периметр основания и апофему |
|
|
Площадь полной поверхности пирамиды через площади боковой поверхности и основания |
|
|
Площадь боковой поверхности правильной усечённой пирамиды через периметры оснований и апофему |
|
|
Объём правильной усечённой пирамиды через площади оснований и апофему |
|
Даже если уверены в своих знаниях, помните: перед ЕГЭ практики не бывает мало. Если отточить навык решения задач, это может сохранить вам баллы. Попробуйте Тренажёр ЕГЭ — сборник заданий экзамена по математике с автопроверкой ответов. Это бесплатно!
