Призма

Что такое призма

Призма — это выпуклый многогранник, две грани которого представляют собой равные многоугольники, расположенные в параллельных плоскостях. Все рёбра, не лежащие в этих плоскостях, параллельны между собой.

Эти два одинаковых многоугольника называют основаниями призмы. Остальные её стороны, которые представляют собой параллелограммы, — боковые грани. Грани этих сторон — это рёбра призмы, они бывают боковыми и рёбрами основания. Места их пересечения друг с другом называются вершинами.

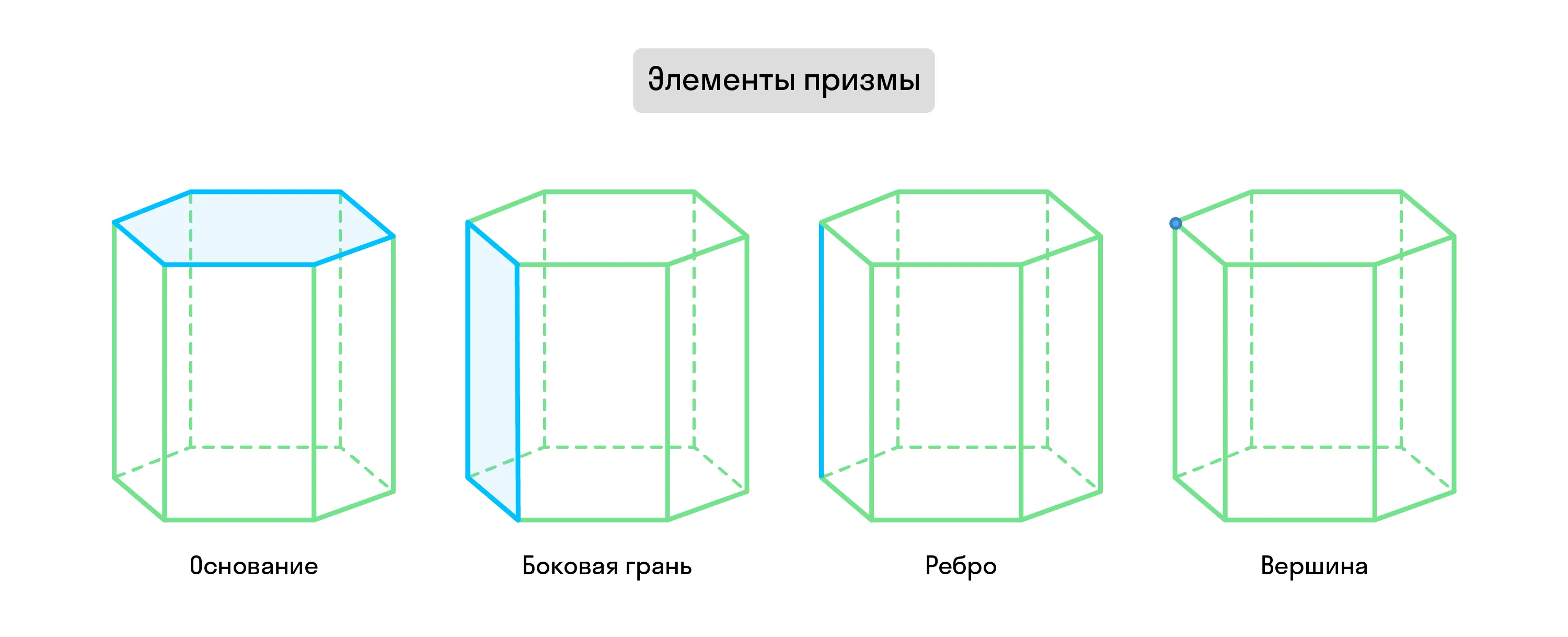
Виды призм и их свойства

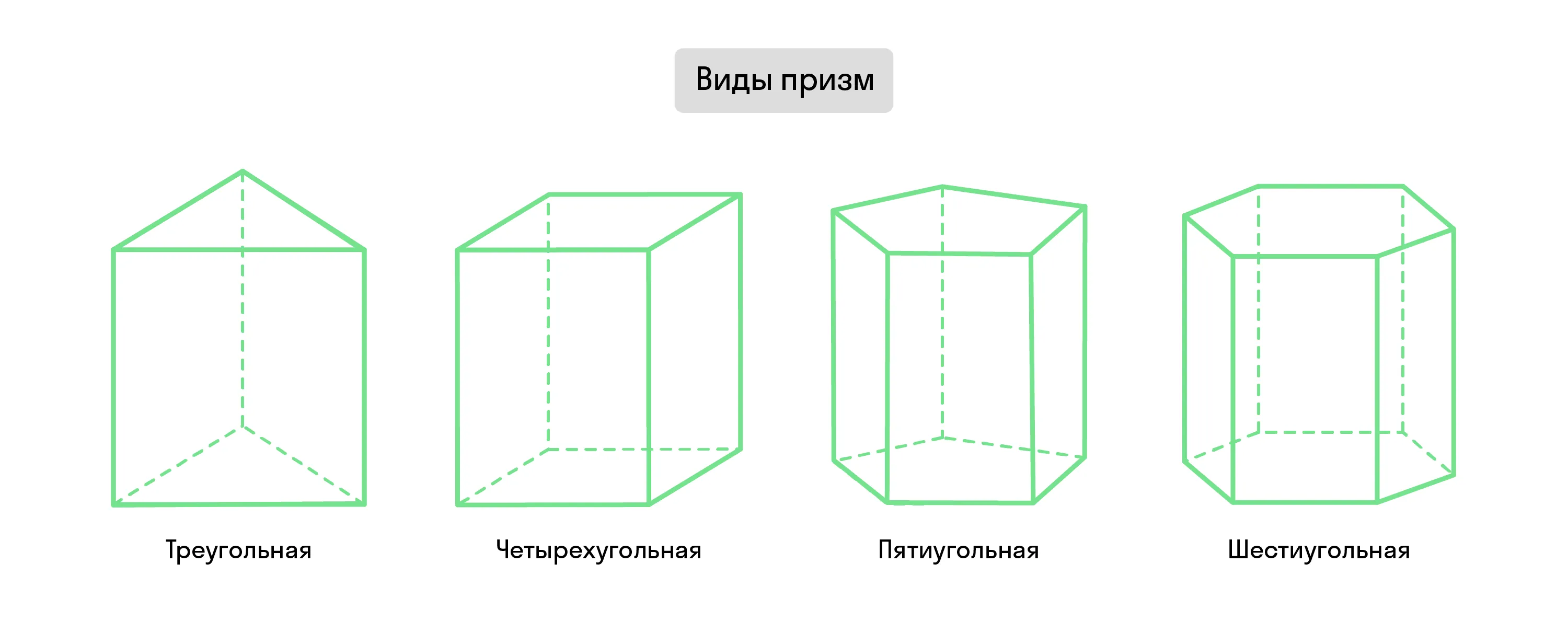
В основаниях призмы могут лежать разные многоугольники: треугольники, четырёхугольники, пятиугольники, шестиугольники и т. д.. В зависимости от этого меняется и вид призмы — она может быть треугольной, четырёхугольной и т. д.

Запомните: боковые рёбра любой призмы равны и параллельны друг другу.

Прямые и наклонные призмы

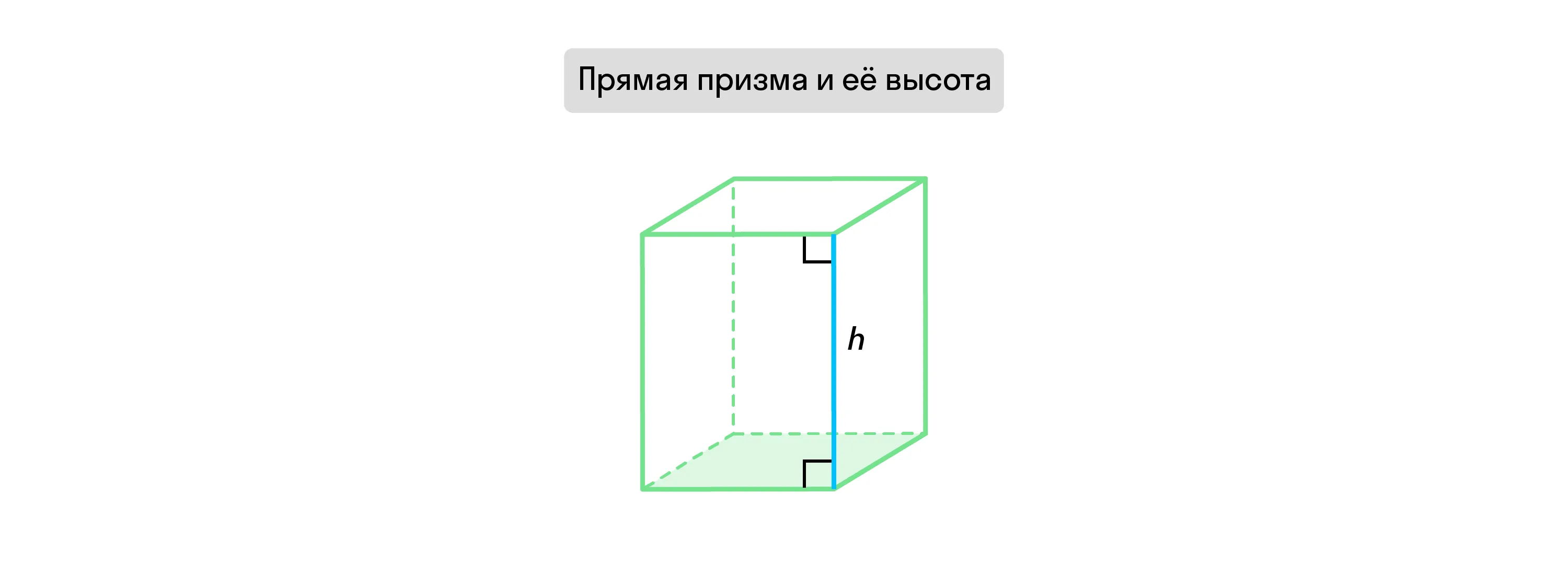
Если боковые рёбра призмы перпендикулярны плоскости её основания, такую фигуру называют прямой призмой.

У такой призмы боковые грани — это прямые четырёхугольники, т. е. прямоугольники и квадраты. Их грани перпендикулярны основаниям призмы, соответственно, угол между её рёбрами и плоскостью основания равен 90°.

Перпендикулярная прямая, проведённая из любой точки одного основания призмы к плоскости другого, называется её высотой. У прямых призм высота совпадает с боковым ребром, т. к. они равны.

Во всех остальных случаях призма считается .наклонной Её боковые грани — это параллелограммы общего вида, т. к. рёбра и основания призмы образуют углы более или менее 90°. При этом высота наклонной призмы всегда меньше длины ребра.

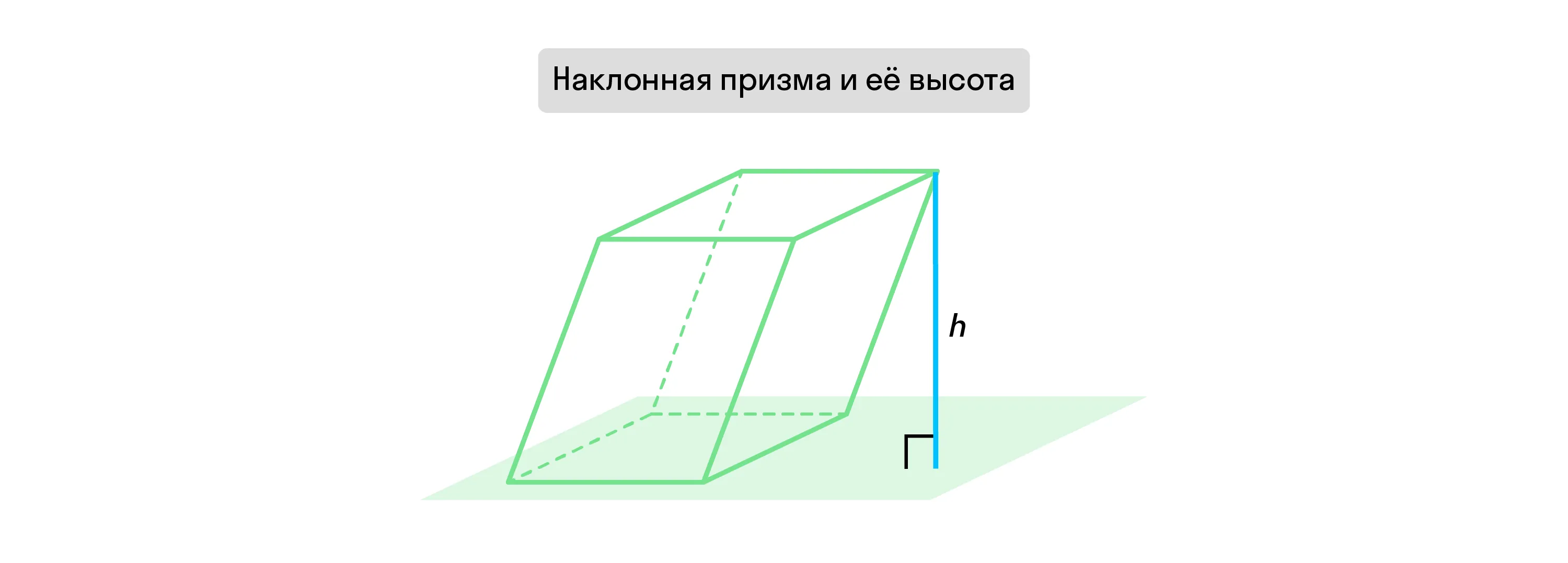
Правильные и неправильные призмы

Если основания призмы — это правильные многоугольники, её тоже называют правильной.

Все , т. е. отрезки, которые соединяют две не принадлежащие одной грани вершины, равны.диагонали При этом они всегда пересекаются в одной точке. Эта точка — центр фигуры, который делит её диагонали пополам.

170.4K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Призма: основные формулы

В таблице ниже оставляем все формулы, которые помогут вам решать задачи с разными видами призм.

Призма: все формулы
Объём призмы через площадь основания и высоту
Объём наклонной призмы через площадь перпендикулярного сечения и длину бокового ребра
Объём правильной прямой призмы через высоту (), длину стороны () и количество сторон ()
Площадь боковой поверхности призмы через периметр основания и высоту
Площадь поверхности призмы через площадь основания, периметр основания и высоту
Площадь поверхности правильной призмы через высоту (), длину стороны () и количество сторон ()

Также советуем не заучивать формулы и определения, а разобраться, как они работают. И самое главное — после этого закрепить знания на практике. Подготовиться к заданиям с призмами, которые ждут вас на экзамене, можно в бесплатном Тренажёре ЕГЭ. Там найдутся тренировочные материалы по этой и другим темам в стереометрии.