Показательные уравнения

Для кого эта статья:

• Читатели, интересующиеся темой статьи
• Специалисты в данной области знаний
• Студенты или школьники, стремящиеся углубить свои знания

Определение показательного уравнения

Показательными называются уравнения, в которых переменная находится в показателе степени. Простейшее уравнение такого вида: a^х = b, где a > 0, a ≠ 1 и a^x = a^y.

Для решения даже простейших показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс тему «Свойства степенной функции» — советуем повторить ее перед тем, как читать дальнейший материал.

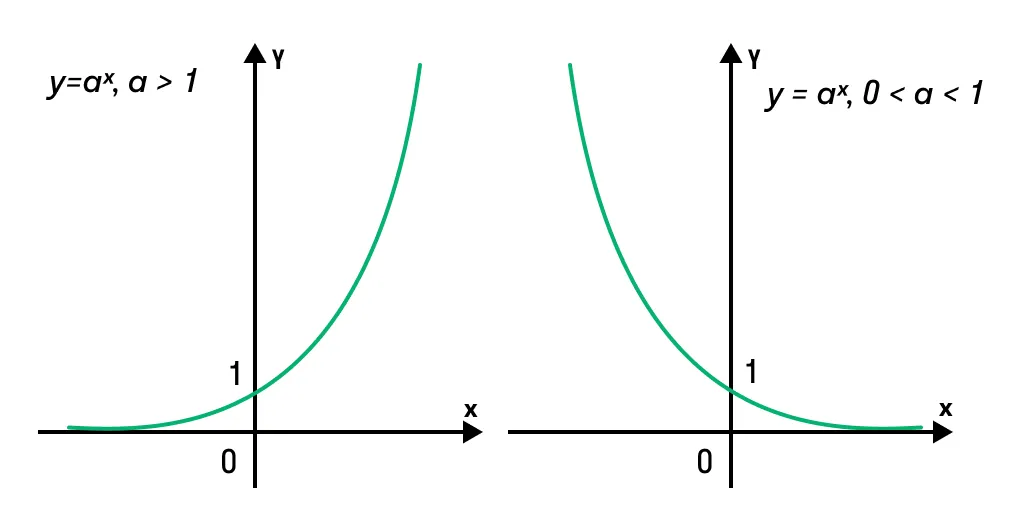
Показательной функцией называют такую: y = a^x, где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a < 1 (но больше 0) — непрерывно убывает. Это хорошо видно на рисунке ниже.

Важно знать

Показательная функция не может быть отрицательным числом, т. е. выражение у = a^x при а ≤ 0 корней не имеет.

Свойства степеней

Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут решать сложные показательные уравнения.

am · an	am+n
am:an	am-n
(a · b)n	an · bn
(a : b)n	an : bn
(an)m	an · m
a−n

Как видите, ничего нового здесь нет, все это проходят в 6–7 классе.

Методы решения показательных уравнений

Самые короткие и простые показательные уравнения решаются легко при помощи свойств степеней. Например:

4^х = 64.

Требуется найти, в какую степень нужно возвести 4, чтобы получить 64.

4 · 4 · 4 = 64

4³ = 64

4^x = 4³

Х = 3

Но как решать показательные уравнения вот такого вида: ? Нужно немного повозиться с преобразованием этого выражения. Например, сделать так, чтобы либо основания, либо степенные показатели стали одинаковы. Для этого мы можем разложить 128 и 4. Вы ведь заметили, что у них есть общий множитель? Правильно, это 2.

Теперь в нашем уравнении появились одинаковые основания, а значит, мы можем приравнять и степени.

В данном случае мы используем один из алгоритмов решения показательных уравнений — привели обе части равенства к одинаковым основаниям. Дальше рассмотрим и другие методы.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

208.5K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Прокачивай знания на курсах математики

• Выбирай из 1200+ репетиторов по математике

• Записывайся на бесплатные курсы для детей

Приведение к одинаковому основанию

Весомую часть уравнений вида а^х = b (при а и b 0) можно решить, превратив b в определенную степень числа a. Именно это мы сделали в примере выше, получив одинаковые основания. Главная трудность в том, чтобы найти у этих чисел общее основание.

Если у нас есть одинаковые основания, но разные показатели степени, то при умножении чисел степени складываются, а при делении — вычитаются.

Пример 1

Рассмотрим еще одно показательное уравнение с корнем.

Мы знаем, что 64 и 8 являются степенями 2. Попробуем использовать это, и тогда 64² = 2¹², а 8 = 2³.

Ответ: .

Пример 2

В этом примере показательного уравнения нужно будет отдельно преобразовать каждую составляющую.

(0,5)^х2 · 4^х+1 = 64^-1

Найдем общее основание показательных функций:

0,5 = 1/2 = 2⁻¹

4 = 2²

64 = 2⁶

В результате у нас получается:

(2⁻¹)^х2 · (2²)^х+1 = (2⁶)⁻¹

2^−х2 · 2^2х+2 = 2⁻⁶

2^−х2+2х+2 = 2⁻⁶

−х² + 2х + 2 = −6

х²− 2х − 8 = 0

Ответ: x = −2; 4.

Приведение к одинаковой степени

Не все показательные уравнения с разными основаниями можно решить предыдущим способом. Иногда проще преобразовать не основания, а показатели степени. Правда, пользоваться этим методом есть смысл только в том случае, когда мы имеем дело с умножением или делением.

При умножении чисел с разными основаниями, но одинаковыми степенными показателями можно перемножить только основания (степень останется прежней): a^xb^x = (ab)^x.

Пример

5^2х−4 = 49^2−х

Общих множителей у левой и правой части уравнения нет и привести их к одинаковому основанию достаточно трудно. Поэтому стоит поработать с показателями степеней:

5^2х−4 = 49^2−х

5^2х−4 = 7^4−2х

5^2х−4 = (1/7)^2х−4

35^2х−4 = 1

2х − 4 = 0

х = 2

Пример 2

2^х−2 = 5^2−х

Нам нужно привести обе части уравнения к одинаковым степенным показателям, и для этого вначале попробуем преобразовать правую часть, используя свойство степенных функций.

2^х−2 = 1/5^х−2

Теперь умножим обе части на 5^2−х и придем к уравнению:

2^х−2 × 5^2−х = 1

10^х−2 = 1

10^х−2 = 10⁰

х − 2 = 0

х = 2

Замена переменной

Суть этого способа решения показательных уравнений проста: мы заменяем «трудную» переменную на более простую и решаем уравнение, а после производим обратную замену. Главное — определить, какую именно переменную стоит заменить.

Пример

4^x- 2^x+1- 8 = 0

Очевидно, что в этом уравнении показательные функции легко привести к общему основанию: 4^х = 2^2х, а 2^х+1 = 2 × 2^х.

2^2х - 2 × 2^х - 8 = 0

Что-то напоминает. 🤔 Если бы из этого выражения можно было волшебным образом убрать 2^х, получилось бы обычное квадратное уравнение. Поэтому мы обозначим 2^х новой переменной — допустим, y.

Если 2^х = y, y > 0, то получается: у²- 2у - 8 = 0.

У такого уравнения есть два корня: у₁ = 4, у₂ = -2.

Проведем обратную замену: 2^х = 4 (подходит по ограничениям).

х = 2.

Ответ: х = 2.

Пример 2

25^х - 6 × 5^х + 5 = 0

Если присмотреться к этому выражению, становится понятно, что у него много общего с квадратным уравнением. Введем новую переменную: 5^х = у, y > 0.

у² - 6у + 5 = 0

Корни такого уравнения: 1 и 5.

Выполним обратную замену:

5^х = 1, значит х = 0.

5^х = 5, значит х = 1.

Ответ: x = 0; 1.

Вынесение общего множителя

В предыдущих примерах мы преобразовывали разные виды показательных уравнений путем разложения многочленов на множители, потому что хотели найти способ решения — получить одинаковые основания или выделить переменную, которую можно заменить.

Общий множитель — это некий многочлен, содержащий переменную, который в скрытом виде присутствует во всех показательных функциях уравнения. Его можно вынести за скобки, чтобы упростить уравнение.

Проблема только в том, чтобы научиться верно определять такое выражение, а этот навык появляется лишь с опытом.

Пример 1

3^х+1 + 3^х - 3^х-2 = 35

Вынесем 3^3-x за скобки и получим:

3^х-2(3³ + 3² - 1) = 35

3^х-2 × 35 = 35

3^х-2 = 1

Поскольку 1 равно любое число в нулевой степени, мы можем записать:

3^х-2 = 3⁰

х - 2 = 0

х = 2

Ответ: х = 2.

Пример 2

5 × 3^-3х+1 + 3^-3х+2 = 24

Для начала мы попробуем в левой части уравнения получить одинаковую степень: 3^-3х+2 = 3^-3х+1+1 = 3 · 3^-3х+1.

Теперь у нас есть общий множитель 3^-3х+1, который можно вынести за скобки, чтобы получить более простое уравнение:

3^-3х+1(5+3) = 24

8 · 3^-3х+1 = 24

3^-3х+1 = 3¹

-3х + 1 = 1

х = 0

Ответ: х = 0.