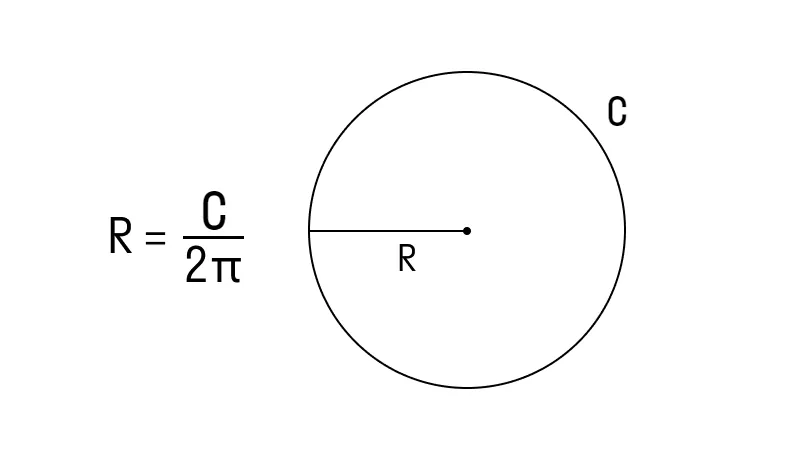
Чтобы найти радиус окружности, нужно знать её диаметр или длину. Радиус равен половине диаметра. Если известна длина окружности, используйте формулу:
Например, если длина окружности 31.4, то радиус равен 5.
Для кого эта статья:
- Студенты и школьники, изучающие математику и геометрию
- Учителя и преподаватели математики
- Все, кто интересуется основами геометрии и основным понятием окружности
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — часть плоскости, которая лежит внутри окружности. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать - как найти длину окружности?

Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Если известна площадь круга
Если известна длина
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Если известен диаметр окружности
Диаметр и радиус — это основные геометрические характеристики окружности.
- Диаметр — отрезок, который соединяет две точки окружности и проходит через её центр.
- Радиус — отрезок, который соединяет центр окружности с любой её точкой.
Примеры: для круга радиусом 5 см, диаметр будет 10 см.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ прямоугольника.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
Получи больше пользы от Skysmart:
-
Подготовься к ОГЭ на пятёрку
-
Подготовься к ЕГЭ на высокие баллы
Записывайся на бесплатные курсы для детей
Решай задания в бесплатном тренажёре ЕГЭ
Если известна сторона описанного квадрата
Сторона описанного квадрата равна диаметру окружности.
Если известны стороны и площадь вписанного треугольника
Если известна площадь и полупериметр описанного треугольника
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Если известна сторона вписанного правильного многоугольника
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.




















