Признаки равенства треугольников - это условия, при которых два треугольника считаются равными.
- Первый признак: по двум сторонам и углу между ними.
- Второй признак: по стороне и двум прилежащим углам.
- Третий признак: по трём сторонам.
Примеры:
- ΔABC = ΔDEF (AB=DE, AC=DF, ∠A=∠D).
- ΔXYZ = ΔPQR (XQ=PQ, ∠X=∠P, ∠Y=∠Q).
- ΔMNO = ΔJKL (MN=JK, NO=KL, MO=JL).
Первый признак равенства треугольников
1 признак равенства треугольников - это если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Пример: треугольники ABC и DEF равны, если:
- AB = DE
- AC = DF
- ∠A = ∠D
Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.
Давайте рассмотрим три признака равенства треугольников.
Теорема 1. Равенство треугольников по двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Даны два треугольника △ABC и △A1B1C1, у которых AC = A1C1, AB = A1B1, ∠A = ∠A1.
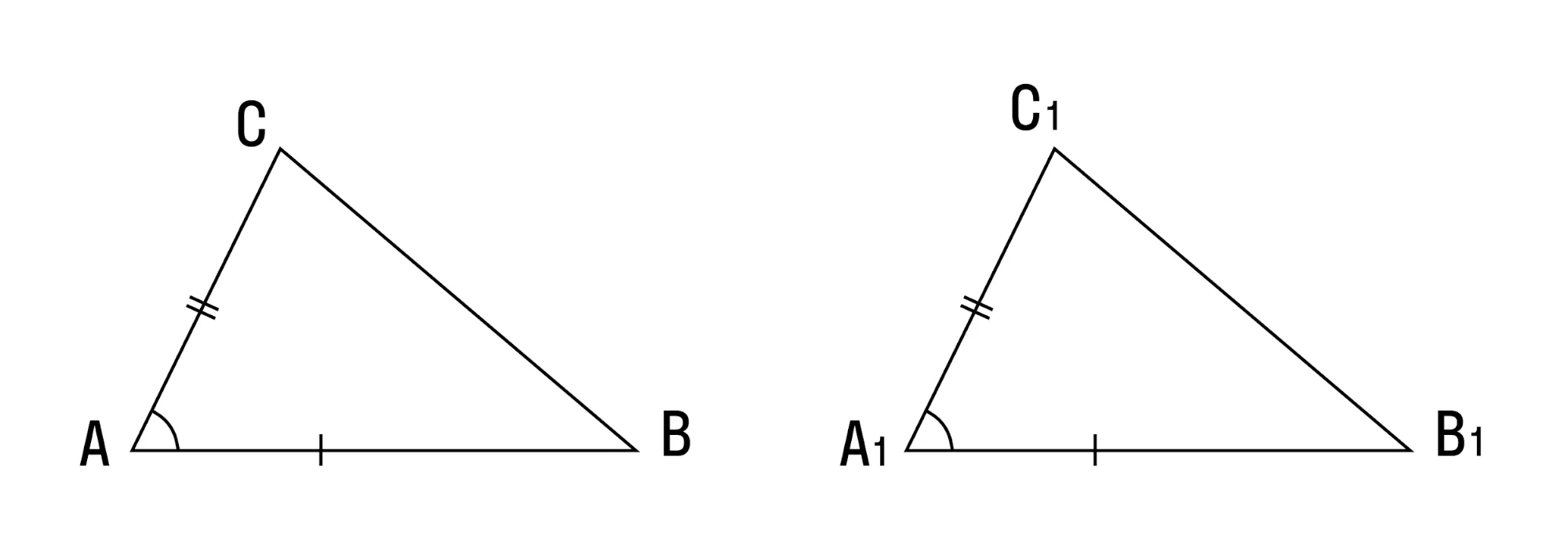
Докажите, что △ABC = △A1B1C1.
Доказательство:
При наложении △A1B1C1 на △ABC вершина A1 совмещается с вершиной A, и сторона A1B1 накладывается на сторону AB, AC — на сторону A1C1.
Сторона A1B1 совмещается со стороной AB, вершина B совпадает с вершиной B1, сторона A1С1 совмещается со стороной AС, вершина C совпадает с вершиной C1.
Значит, происходит совмещение вершин В и В1, С и С1.
B1C1 = BC, следовательно, △ABC совмещается с △A1B1C
Теорема доказана.
Познавайте математику вместе с нашими лучшими преподавателями на курсах по математике для учеников с 1 до 11 класса!
Второй признак равенства треугольников
Второй признак равенства треугольников — это условие, при котором два треугольника считаются равными, если у них одна сторона и два прилежащих к этой стороне угла равны соответственно одной стороне и двум прилежащим к этой стороне углам другого треугольника.
Пример:
- ΔABC и ΔDEF, если AB=DE, ∠A=∠D, ∠B=∠E, то ΔABC = ΔDEF.
Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Даны два треугольника △ABC и △A1B1C1, у которых:
AC = A1C1, ∠A = ∠A1, ∠C = ∠C1.
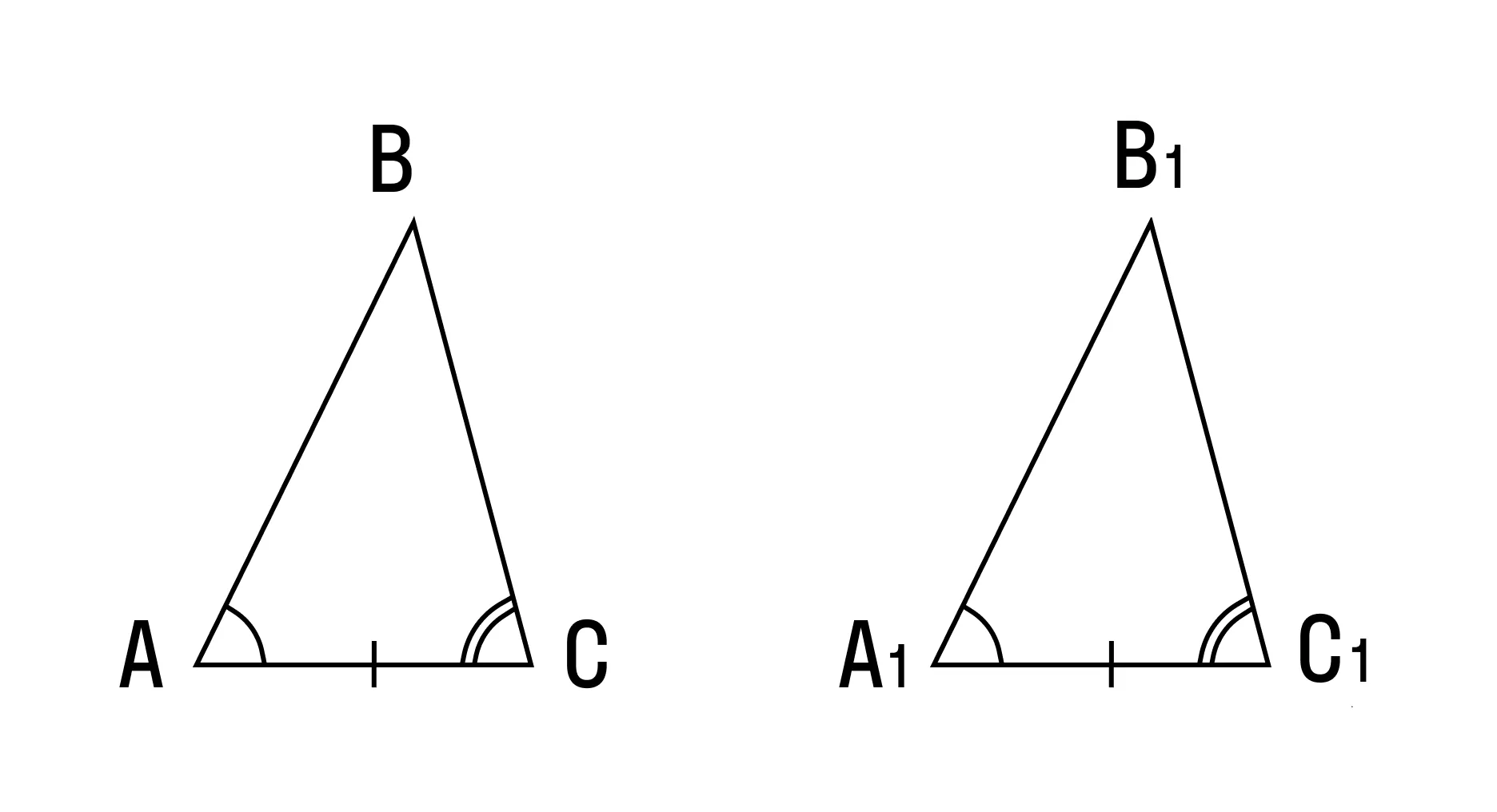
Докажите, что △ABC = △A1B1C1.
Доказательство:
Путем наложения △ABC на △A1B1C1, совмещаем вершину А с вершиной A1, вершины В и В1 лежат по одну сторону от А1С1.
Тогда АС совмещается с A1C1, вершина C совпадает с C1, поскольку мы знаем, что АС = A1C1.
AB накладывается на A1B1, поскольку мы знаем, что ∠A = ∠A1.
CB накладывается на C1B1, поскольку мы знаем, что ∠C = ∠C1.
Вершина B совпадает с вершиной B1.
Если АВ совмещается с А1В1, ВС совмещается с В1С1, то △ABC совмещается с △A1B1C1, значит, △ABC = △A1B1C1 .
Теорема доказана.
Пройдите тест и узнайте, какие темы отделяют от пятёрки по математике
Добро пожаловать в школу магии.
О нет! Мальчик-молния случайно попал в школьные часы. Теперь они отстают. Мы все можем задержаться в школе
Жми на стрелки сверху, чтобы путешествовать в истории→
Одна ученица когда-то была в школьной кладовке и видела там схему часов
Но в кладовку просто так не попадёшь→
Реши два примера от волшебной статуи на входе в кладовку
Схема у нас!
Деталь можно сделать из проволоки и формы для заливки металла. Найди их на картинке
Теперь осталось взять инструменты у садовника! Он обменяет их на волшебные бобы для его сада
Для починки часов нужны: молоток, отвертка и плоскогубцы.
Ты можешь либо одолжить у садовника набор, либо отдельные инструменты, либо и то, и другое. Какое минимальное количество волшебных бобов ты можешь отдать садовнику?
Деталь имеет форму прямоугольника со сторонами 5 см и 12 см. Найди периметр и площадь детали, чтобы посчитать, сколько проволоки для неё понадобится
Периметр прямоугольника равен
Площадь прямоугольника равна
Мальчик-молния выплавил деталь, часы должны работать! Но они почему-то не идут... Кажется, одной шестерёнки не хватает — она куда-то упала
В коробке, шкатулке, ящике и банке находятся пыльца, волчий корень, золото и шестерёнка. Шестерёнка и пыльца не в коробке, ёмкость с волчьим корнем стоит между ящиком и ёмкостью с золотом, в банке не волчий корень и не шестерёнка. Шкатулка стоит около банки и ёмкостью с пыльцой. В какой ёмкости что находится?
Соедини ёмкости с содержимым на картинках ниже
Ура, мы вставили последнюю шестеренку, и часы пошли! Сегодня уроки закончатся вовремя. Спасибо тебе за помощь!
Дальше узнаешь свои результаты →
Получи больше пользы от Skysmart:
-
Прокачивай знания на курсах математики.
-
Выбирай из 1200+ репетиторов по математике.
Записывайся на бесплатные курсы для детей.
Третий признак равенства треугольников
ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ: Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. Например, если в треугольнике ABC стороны:
- AB = XY,
- BC = YZ,
- CA = ZX,
то треугольники ABC и XYZ равны.
Теорема 3. Равенство треугольников по трем сторонам.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Даны два треугольника △ABC и △A1B1C1, у которых:
AC = A1C1,
AB = A1B1,
CB = C1B1.
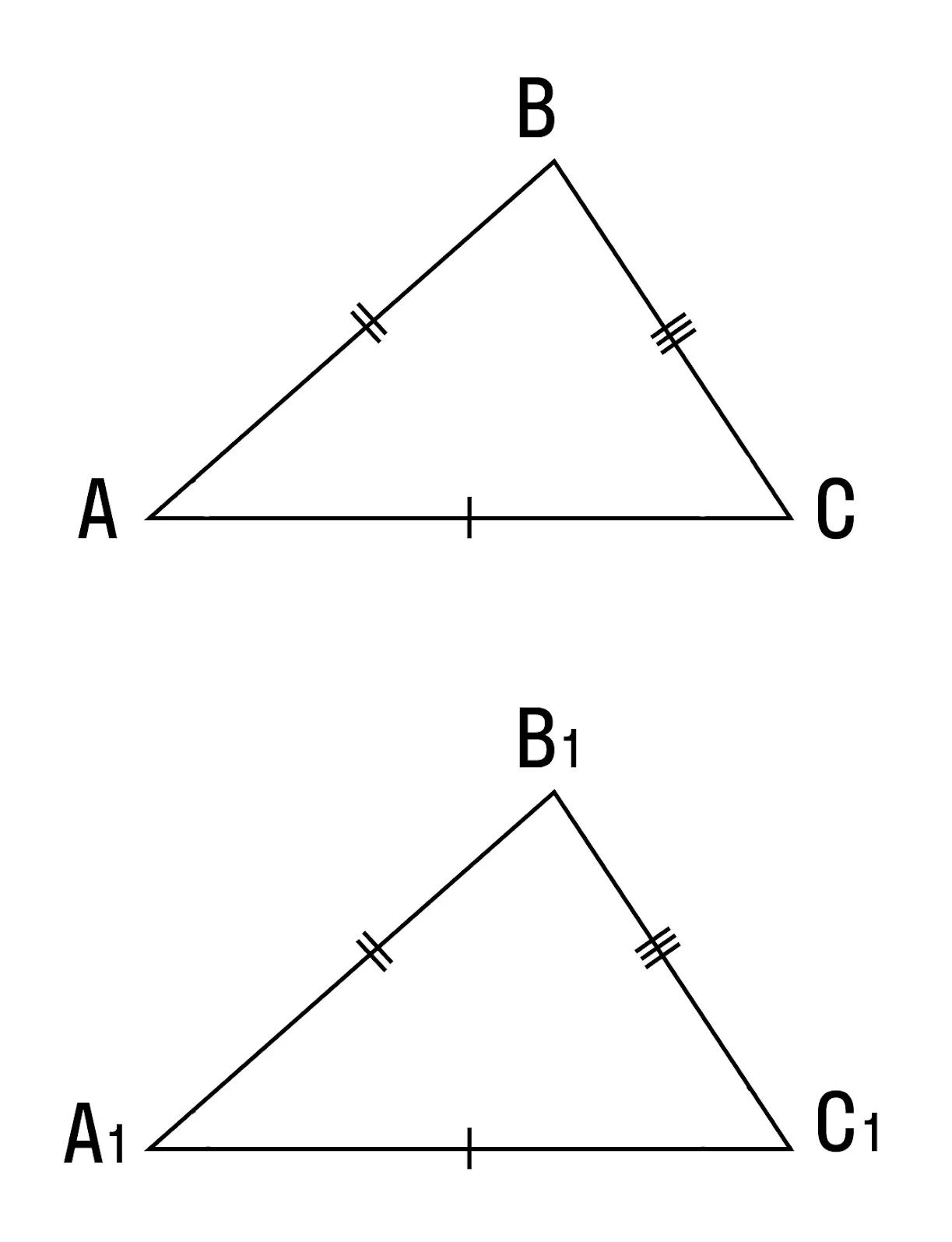
Докажите, что △ABC = △A1B1C1.
Доказательство 3 признака равенства треугольников:
Приложим △ABC к △A1B1C1 таким образом, чтобы вершина A совпала с вершиной A1, вершина B — с вершиной B1, вершина C и вершина C1 лежат по разные стороны от прямой А1В1.
AC = A1C1, BC = B1C1, то △A1C1С и △B1C1С — равнобедренные.
∠1=∠2, ∠3=∠4 (по свойству равнобедренного треугольника), значит,
∠A1СB1 = ∠A1C1B1.
AC = A1C1, BC = B1C1.
∠C = ∠C1, тогда △ABC = △A1B1C1 (по первому признаку равенства треугольников).
Теорема доказана.
Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.
Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.
- Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
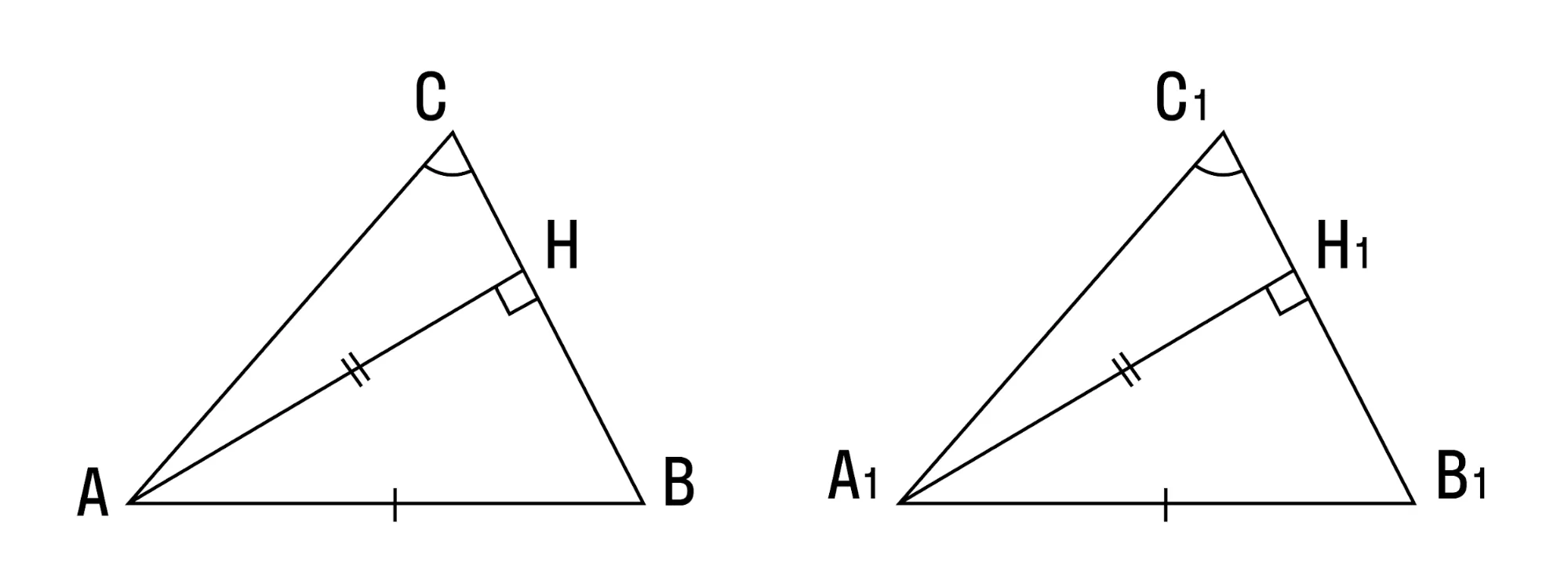
- Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
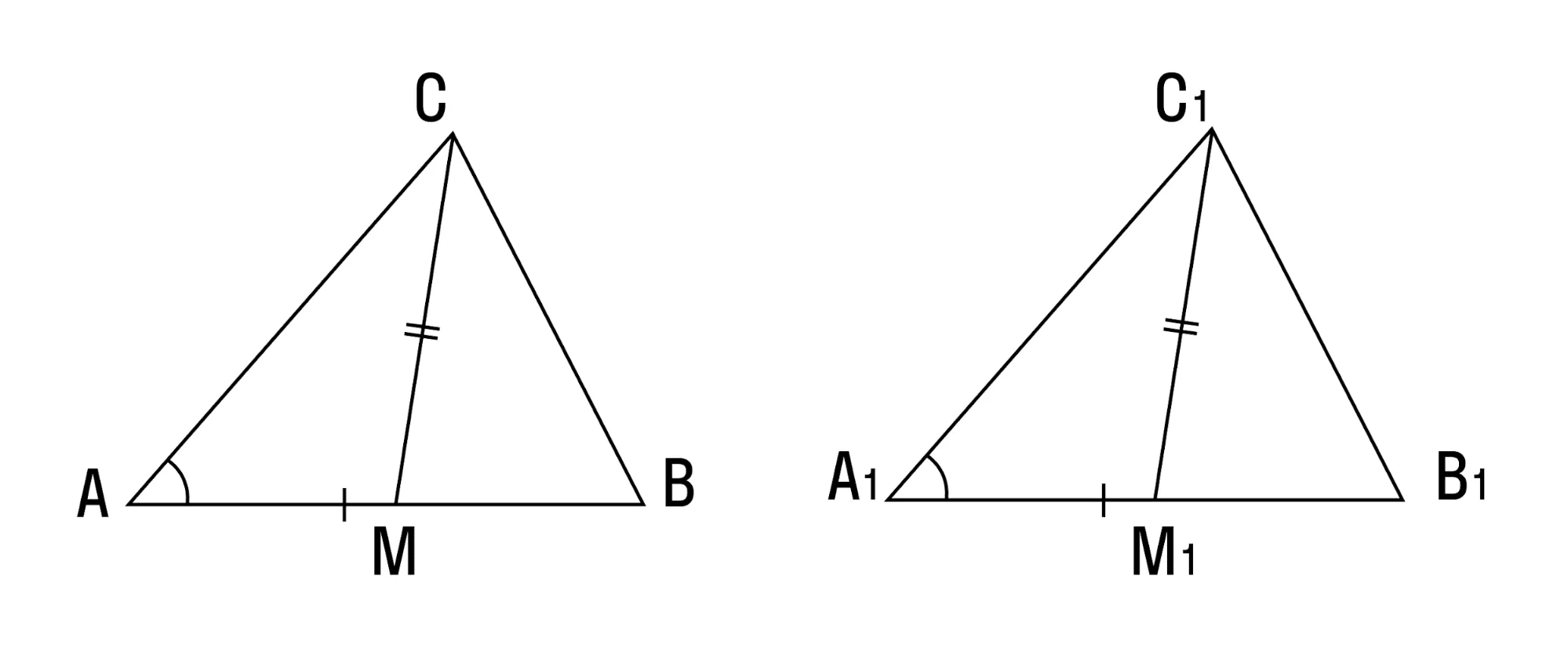
- Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
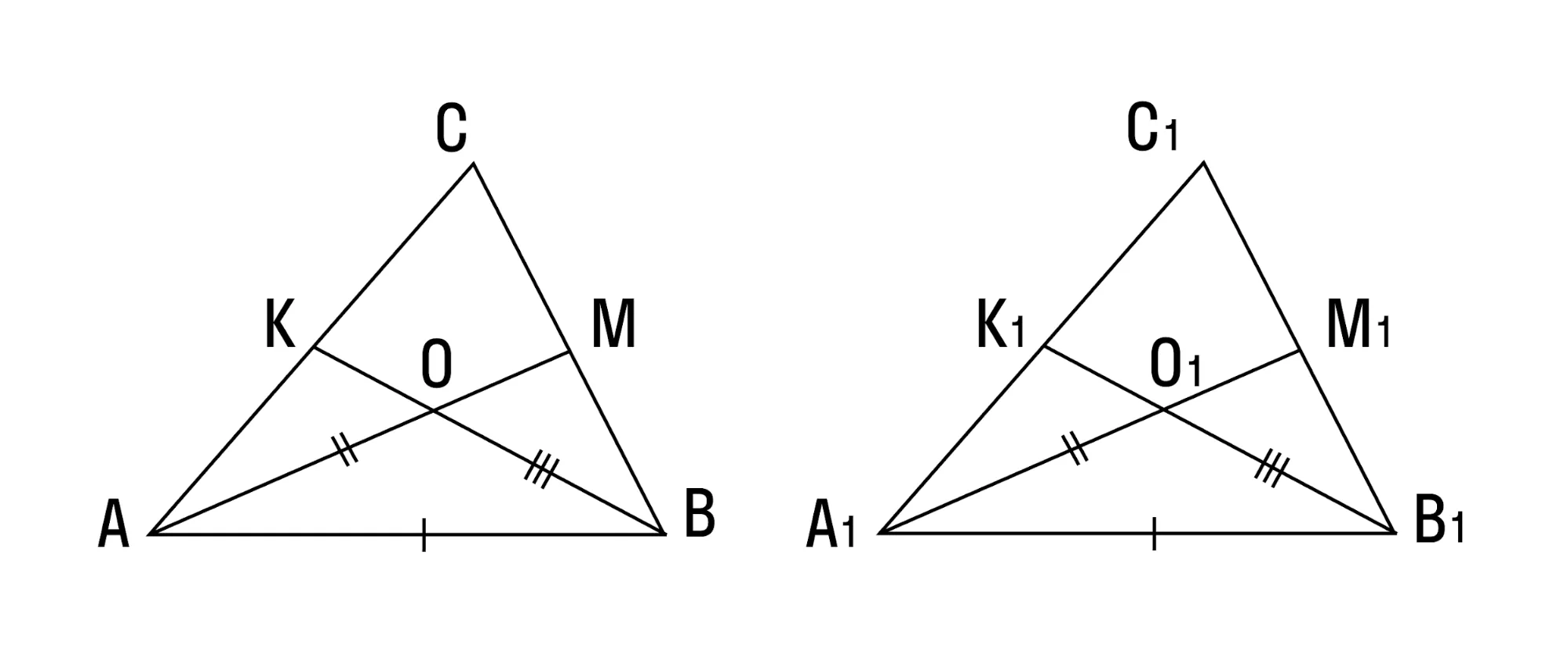
- Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
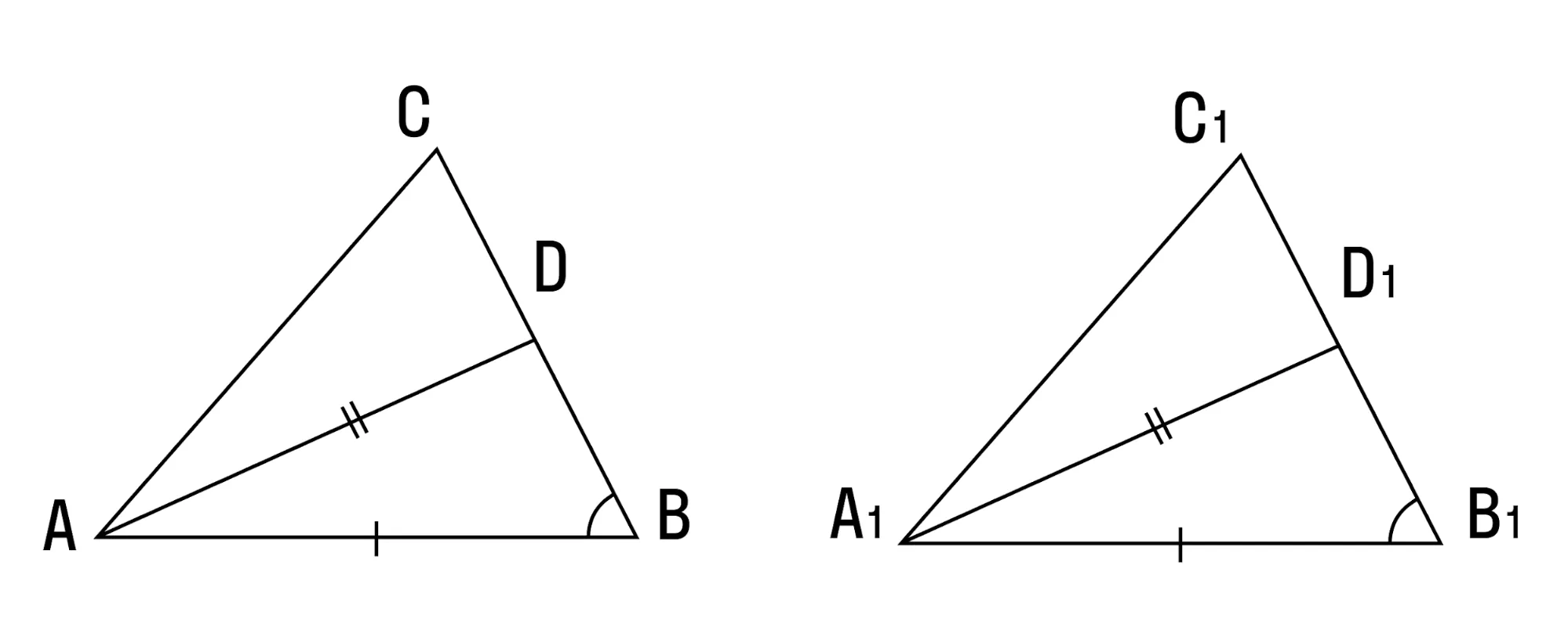
- Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.
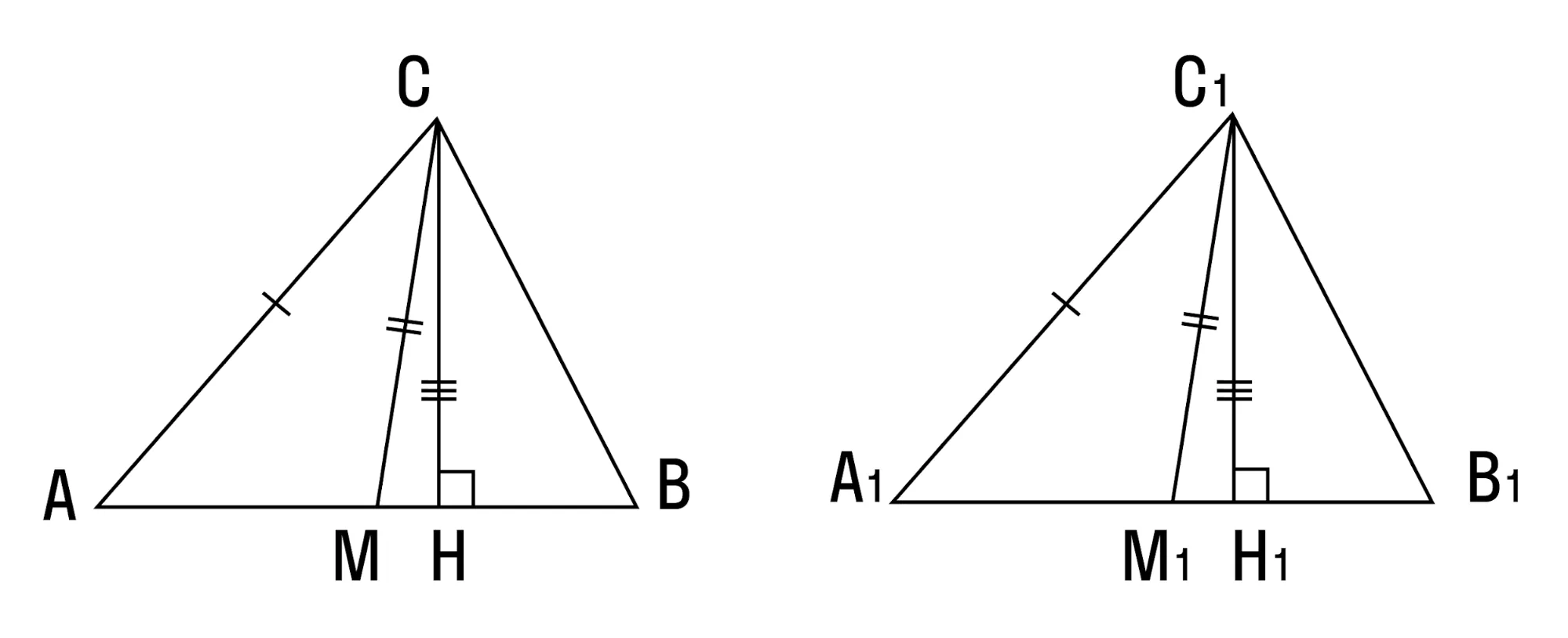
Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.
