Деление дробей — это операция, в которой первая дробь умножается на перевернутую вторую дробь. Например, для дробей
Пример:
Понятие дроби
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b.
Существует два формата записи:
обыкновенный вид — 1/2 или a/b,
десятичный вид — 0,5.
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление. В 5 классе ребята это уже знают.
Дроби бывают двух видов:
Числовые — состоят из чисел, например, 5/9 или (1,5 - 0,2)/15.
Алгебраические — состоят из переменных, например, (x + y)/(x - y). В этом случае значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается —
Основные свойства дроби
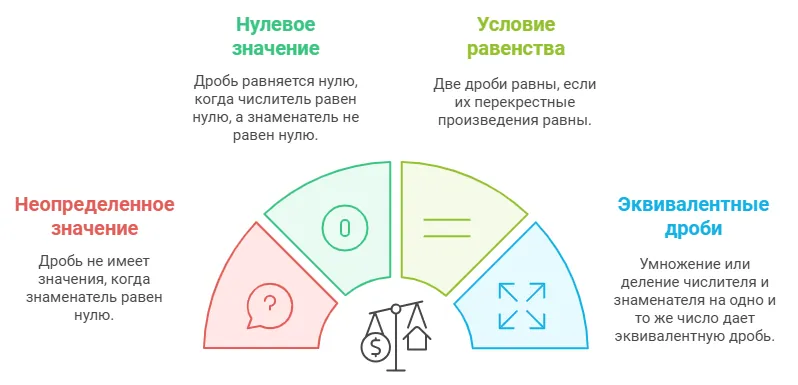
1. Дробь не имеет значения, при условии, если знаменатель равен нулю.
2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
3. Две дроби a/b и c/d называются равными, если a * d = b * c.
4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Получи больше пользы от Skysmart:
-
Прокачивай знания на курсах математики.
-
Выбирай из 1200+ репетиторов по математике.
Записывайся на бесплатные курсы для детей.
Деление дробных чисел
Деление — арифметическое действие, по которому можно узнать, сколько раз одно число содержится в другом. А еще деление — это обратное действие умножения.
Свойства деления:
При делении на единицу получится такое же число: a : 1 = a.
На ноль делить нельзя.
При делении нуля на что-либо получится ноль: 0 : a = 0.
При делении числа на само себя получится единица: a : a = 1.
При деления суммы на какое-либо число, можно разделить на него каждое слагаемое и сложить полученные результаты: (a + b) : c = a : c + b : c.
При делении разности на какое-нибудь число, можно разделить на него уменьшаемое и вычитаемое отдельно и из первого частного вычесть второе: (a - b) : c = a : c - b : c.
При делении произведения двух множителей на число, можно разделить на него любой из множителей и частное умножить на второй множитель: (a * b) : c = (a : c) · b = a * (b : c).
Деление обыкновенных дробей
Как делить дробь на дробь? Выполняем следующую последовательность действий:
числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Как делить дроби с разными знаменателями? Тут все просто: пользуемся правилами выше, поскольку на практике нам не важно, одинаковые знаменатели или нет.
Деление дроби на натуральное число
Чтобы разделить дробь на целое число, нужно умножить знаменатель дроби на это число, оставив числитель без изменений. Например, чтобы разделить
Для деления дроби на натуральное число нужно:
представить данный делитель в виде неправильной дроби, где числитель равен этому числу, а знаменатель единица;
произвести деление по предыдущему правилу.
Деление натурального числа на дробь
Чтобы поделить натуральное число на обыкновенную дробь нужно:
делимое записать в виде дроби;
умножить полученную дробь на дробь, обратную делителю, воспользовавшись алгоритмом, который мы уже разобрали выше.
Деление на смешанное число
Для деления смешанных чисел необходимо:
представить числа в виде неправильных дробей
выполнить деление с полученными дробями.
