Разложение чисел на простые множители

Зачем раскладывать число на простые множители

А ведь и правда интересно, стоит ли вообще изучать эту тему или в жизни она не пригодится? Насколько полезен навык разложения числа на множители?

Вопрос очень хороший! Математические задачки прекрасно развивают логику и умение мыслить нестандартно, что пригодится в любой профессии. К тому же в математике многие темы словно ступеньки, ведущие к более объемным и сложным. Вот и предмет нашего обсуждения не исключение.

Когда вы научитесь раскладывать число на простые множители, то:

• заодно повторите понятие «простые множители»;

• вспомните тему «Признаки делимости»;

• сможете находить наименьшее общее кратное;

• поймете, как можно сокращать дроби и находить общий множитель.

И это только разделы, с которыми вы познакомитесь в 6-м классе. Представляете, сколько еще ждет впереди! Как видно, плюсов от изучения темы достаточно много, — давайте же начнем.

Вспоминаем, что такое простые множители

Первое, с чем стоит разобраться, — это само понятие «простой множитель». Помните, что это такое?

Множитель — это число, которое показывает, сколько раз нужно повторить слагаемым какое-нибудь другое число (множимое), чтобы получить произведение.

Так, в примере 2 × 7 = 14 число 2 называют первым множителем, число 7 — вторым множителем, а 14 — произведением, или значением произведения.

В уравнении 5х = 20 число 5 можно назвать известным множителем, х — неизвестным множителем, 20 — значением произведения.

Простое число — это число, которое делится только на само себя и единицу.

Попробуем перечислить все простые числа от 1 до 10: 3, 5, 7.

А число 9 простое? Нет, так как, помимо 1 и 9, число делится на 3.

А число 8? Нет, так как восьмерка делится на 1, 8, 2 и 4.

Как вы думаете, сколько простых чисел существует?

Правильно, бесконечное множество! Разумеется, весь этот числовой ряд выучить не получится. Но есть две хорошие новости: во-первых, нам и не нужно знать все это множество, математики давно составили таблицы простых чисел (от 1 до 100, от 1 до 1 000), которыми мы можем воспользоваться в любой момент. А самое главное, зная алгоритм проверки числа, мы можем самостоятельно установить, является ли оно простым.

Один из способов проверки — метод перебора делителей. Для этого нам необходимо проверить делимость числа на разные другие числа. Если подобрать дополнительные делители для числа получится — оно составное, а если среди его делителей будет только единица и оно само — то простое.

201.6K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Прокачивай знания на курсах математики.

• Выбирай из 1200+ репетиторов по математике.

• Записывайся на бесплатные курсы для детей.

Понятие разложения на простые множители

Итак, с основными понятиями мы разобрались. Что же тогда означает «разложить число на простые множители»?

Разложить на простые множители — значит представить число в виде произведения простых множителей (чисел).

Например:

20 = 2 × 2 × 5;

99 = 11 × 3 × 3;

126 = 2 × 2 × 31;

1 084 = 2 × 2 × 271.

Разложение на простые множители можно сравнить с разменом купюры. Представьте, что вам захотелось купить газировку из автомата, а он принимает только монеты. Вы идете в магазин и просите разменять купюру, продавец выдает вам целую стопку монет разного номинала. Среди всего количества будут повторы: несколько рублевых, парочка пятирублевых, горсть десяток. Теперь можно бежать к автомату: какой напиток возьмем, вишневый или грушевый?

Возможно, кто-то сейчас начал волноваться и переживать, что ошибется при выполнении разложения. Спешим успокоить!

В арифметике есть теорема: любое натуральное число n, большее единицы, можно разложить на произведение простых чисел, причем это разложение единственно с точностью до порядка следования сомножителей.

А значит, каким бы способом разложения вы ни воспользовались, все равно придете к верному ответу — при условии, что все множители в произведении будут простыми.

Практика

Теперь про способы разложения. В школе на уроках математики часто пользуются методом, который заключается в записывании множителей столбиком, этаком последовательном делении. Мы перебираем простые множители по порядку, начиная с числа 2, и делим на них число до тех пор, пока от него не остается единичка.

Задачка 1

Разложим число 52 на простые множители:

1. Начинаем перебор простых множителей. 52 точно делится на 2, так как является четным: 52 : 2 = 26.

2. Получившийся ответ 26 также делится на 2: 26 : 2 = 13.

3. Число 13 не делится ни на 2, ни на 3, ни на 5. Перебирая ряд простых чисел, мы сможем разделить 13 только на само себя, а значит, это число — простое.

Наглядно это записывается таким образом:

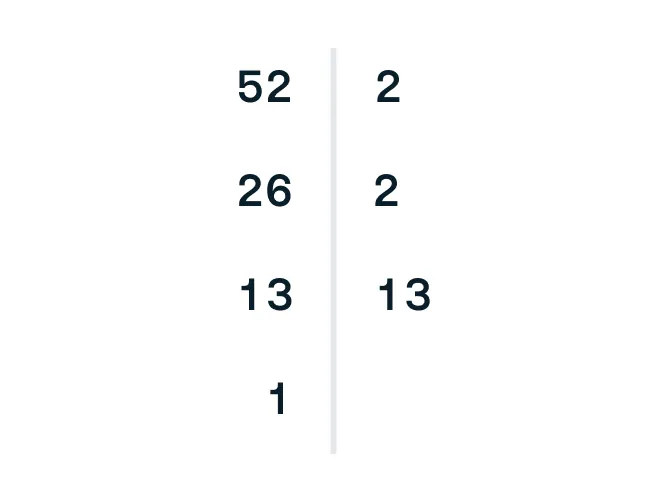
Разложение прошло успешно!

52 = 2 × 2 × 13.

«Practice makes perfect», — говорят в Англии, что означает «Практика приводит к совершенству». Давайте продолжим решать задачи и подытожим разбор метода алгоритмом, которым вы сможете воспользоваться на уроках математики.

Задачка 2

Разложим число 63 на простые множители:

1. Начинаем перебор простых множителей. 63 не делится на 2, а вот на 3 — прекрасно! 63 : 3 = 21.

2. Число 21 вновь не делится на 2, так как является нечетным. Следующий простой множитель — это 3, проверяем делимость на него: 21 : 3 = 7.

3. Перебираем ряд простых чисел и делим на них число 7. Без остатка 7 делится только на само себя: 7 : 7 = 1.

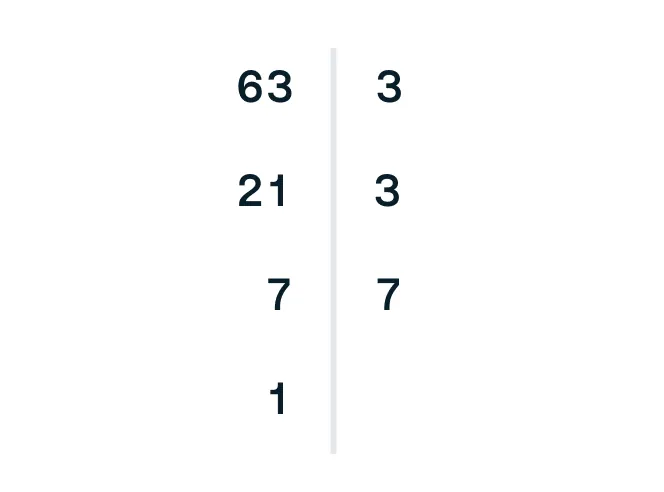
63 = 3 × 3 × 7.

Задачка 3

Разложим число 128 на простые множители:

1. 128 точно делится на 2: 128 : 2 = 64.

2. Число 64 тоже является четным, а значит, 64 : 2 = 32.

3. Продолжаем делить на два: 32 : 2 = 16.

4. Еще немножко: 16 : 2 = 8.

5. 8 : 2 = 4.

6. 4 : 2 = 2.

7. 2 : 2 = 1.

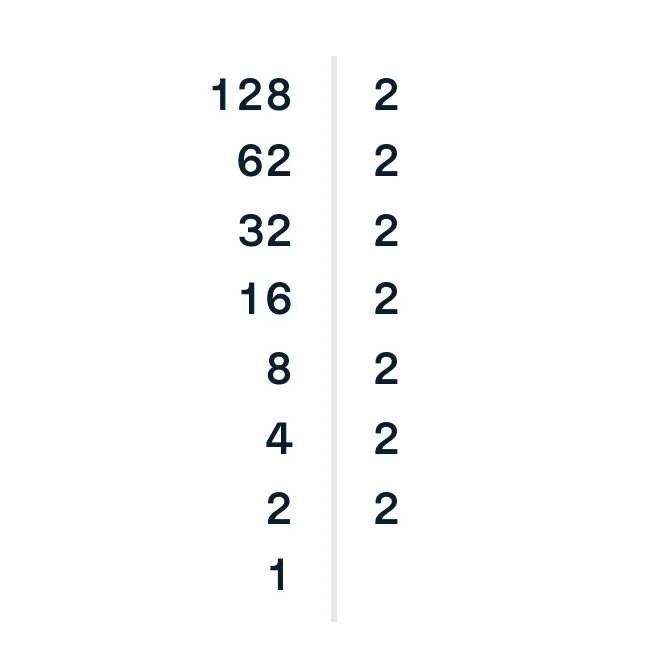
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2, или же 128 = 2⁷. О втором виде записи поговорим чуть ниже.

Задачка 4

Разложим число 37 на простые множители.

Перебирая простые множители от 1 до 37, мы не найдем ни одного числа, кроме самого 37, которое бы делилось на него без остатка. Значит, число 37 простое и разложение провести невозможно.

37 = 37.

Алгоритм разложения числа на множители

Время подвести промежуточный итог и составить алгоритм разложения числа на множители:

1. В первый столбик записываем исходное число.

2. Во второй столбик, напротив первого числа, записываем наименьший простой множитель, на который исходное число делится без остатка (идем по порядку ряда простых чисел: 2, 3, 5, 7 и т. д.).

3. В первый столбик записываем результат деления и вновь ищем наименьший простой множитель, на который это число делится без остатка.

4. Проводим разложение до тех пор, пока в левом столбике не запишем число 1.

Каноническая запись

В теме «Разложение на простые множители» встречается понятие «канонический вид» или «каноническая запись». Что означают эти страшные слова?

Канонический вид — это такой тип записи, который иначе можно назвать стандартным, общепринятым. То есть такой, что где бы вы ни показали записанное, вас обязательно поймут — и в Индии, и в Китае, и даже в Арктике (при условии, что вы показываете записи математикам, конечно).

Это как показать любому ученому химическую формулу Н₂О: это каноническая, общепринятая запись для обозначения молекулы воды.

Но вернемся к простым множителям. Думаем, вы уже заметили, что при разложении могут повторяться одни и те же числа. Так, при разложении числа 128 мы получили аж семь двоек! Для упрощения записи произведение одинаковых множителей записывают с помощью степени.

Степень — это число, которое показывает, сколько раз множитель был умножен сам на себя.

5² = 5 × 5.

7³ = 7 × 7 × 7.

10⁴ = 10 × 10 × 10 × 10.

Таким образом, запись разложения на простые множители будет выглядеть так:

63 = 3² × 7;

52 = 2² × 13;

32 = 2⁵.

Применение признаков делимости при разложении на простые множители

Последний нюанс, который нам нужно обсудить, — это применение признаков делимости при разложении на простые множители. Иными словами, как определить, что число делится на 3, или на 7, или на другие числа, не прибегая непосредственно к делению?

Почему это важно? Порой при поиске простых делителей нам приходится перебирать число за числом, что достаточно долго и энергозатратно. Математики (и программисты тоже) всегда стремятся упростить задачу, найти более легкое решение. А зная свойства делимости, как раз можно ускорить процесс разложения.

Для начала давайте вспомним: как определить, на что делится число? Приведем некоторые примеры.

Признак делимости на…	Правило	Примеры
2	Число четное, оканчивается на 0, 2, 4, 6, 8	10, 24, 12 658: 10 : 2 = 5; 24 : 2 = 12; 12 658 : 2 = 6 329
3	Сумма цифр делится на 3	24, 63, 102: 24 : 2 + 4 = 6, а 6 делится на 3, значит, 24 делится на 3; 63 : 6 + 3 = 9, а 9 делится на 3, значит, и 63 делится на 3; 102 : 1 + 0 + 2 = 3, а 3 делится на 3, значит, и 102 делится на 3
4	Последние две цифры — нули или образуют число, которое делится на 4	100, 1 024: 100 : 4 = 25; 1 024 : 24 делится на 4, значит, и 1024 : 4 = 256
5	Оканчивается на 0 или 5	15, 105, 1 200: 15 : 5 = 3; 105 : 5 = 21; 1 200 : 5 = 240
6	Делится на 2 и на 3	36: делится на 2, так как является четным; делится на 3, так как сумма цифр 3 + 6 = 9 делится на 3 72: делится на 2, так как является четным; делится на 3, так как сумма цифр 3 + 6 = 9 делится на 3
7	Разность числа без последней цифры и удвоенной последней цифры делится на 7	343: 34 − 3 × 2 = 34 − 6 = 28; 28 делится на 7, значит, и 343 : 7 = 49
8	Последние три цифры — нули или образуют число, которое делится на 8	12 000 : 8 = 1 500; 1 320 : 8 = 165; 1 567 488 : 8 = 195 936
9	Сумма цифр делится на 9	252 делится на 9, так как 2 + 5 + 2 = 9; 9 900 делится на 9, так как 9 + 9 + 0 + 0 = 18
10	Оканчивается на 0	50 : 10 = 5; 600 : 10 = 60; 75 460 : 10 = 7 546

Кстати, чтобы определить, делится ли число на составной множитель, нужно проверить, делится ли оно на простые множители, входящие в его состав.

Например, чтобы проверить, делится ли число на 14, нужно определить, можно ли его разделить на 2 и на 7. А число, делящееся на 27, будет делиться одновременно и на 3, и на 9.

Попробуем применить знание о делимости к разложению на множители.

Задачка 5

Разложим на множители число 5 600:

1. Так как число оканчивается на два нуля, оно точно делится на 100. 100 = 25 × 4 = 5 × 5 × 2 × 2.

2. Число 56 не делится на 3 (т. к. 5 + 6 = 11), 4, 5, 6, зато делится на 7. 56 = 7 × 8 = 7 × 2 × 2 × 2.

3. Значит, 5 600 = 56 × 100 = 7 × 8 × 25 × 4 = 7 × 2 × 2 × 2 × 5 × 5 × 2 × 2. В каноническом виде 5 600 = 2⁵ × 5² × 7.

Задачка 6

Разложим на множители число 364:

1. Оно оканчивается на число 64, которое, в свою очередь, делится на 4. Значит, и само число делится: 364 : 4 = 91.

2. Число 91 не делится на 2, 3, 4, 5, 6, но делится на 7: 91 : 7 = 13.

3. 364 = 4 × 7 × 13 = 2² × 7 × 13.

Задачка 7

Разложим на множители число 750:

1. Число оканчивается на 0, а значит, делится на 10. 10 = 2 × 5.

2. 75 делится на 3 (7 + 5 = 12): 75 : 3 = 25.

3. 750 = 75 × 10 = 25 × 3 × 2 × 5 = 5 × 5 × 3 × 2 × 5 = 5³ × 2 × 3.

Арифметика как наука завораживает своей простотой и изящностью. Из десяти цифр складывается бесконечное множество чисел, которые взаимодействуют друг с другом, рождая закономерности и правила. Больше о царице наук вы сможете узнать на курсах профильной математики в онлайн-школе Skysmart. На уроках вы получите ответы на вопросы: «Откуда взялось число пи?», «Как получить бесконечную десятичную дробь?», «Что значит округлить по избытку?» и многие другие. Интересно? Тогда с нетерпением ждем вас!