Действительные числа

Определение действительных чисел

Рациональные числа объединяют в себе целые числа и дробные числа. А действительные числа объединяют рациональные и иррациональные числа. Отсюда сформулируем определения различных видов чисел:

Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Множество рациональных чисел — .

Иррациональное число — это число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби m/n. Оно может быть выражено в форме бесконечной непериодической десятичной дроби. Примеры иррациональных чисел — .

Множество действительных (вещественных) чисел состоит из множества рациональных и множества иррациональных чисел. Оно обозначается буквой , а также его можно записать как (-∞; +∞). Можно записать так, что есть объединение двух множеств: рациональных и иррациональных чисел: .

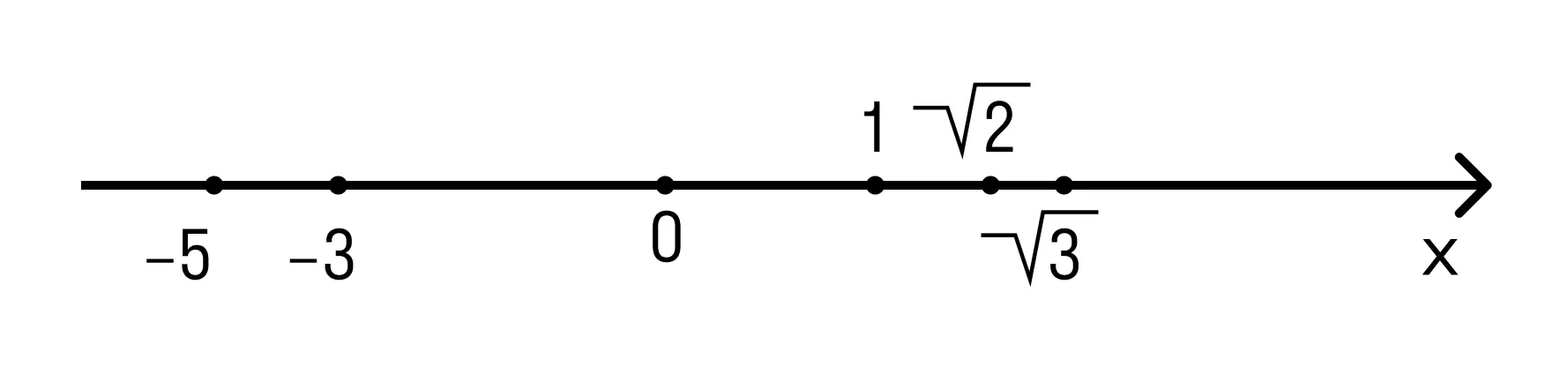
Примеры действительных чисел:

.

Действительные числа могут быть как положительными, так и отрицательными, а также нулем.

При помощи действительных чисел можно описать величины, значения которых могут изменяться непрерывно. Проще говоря, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное значение этой величины.

Действительные числа на координатной прямой

Координатная прямая — это прямая с заданным началом отсчета, единичным отрезком и направлением.

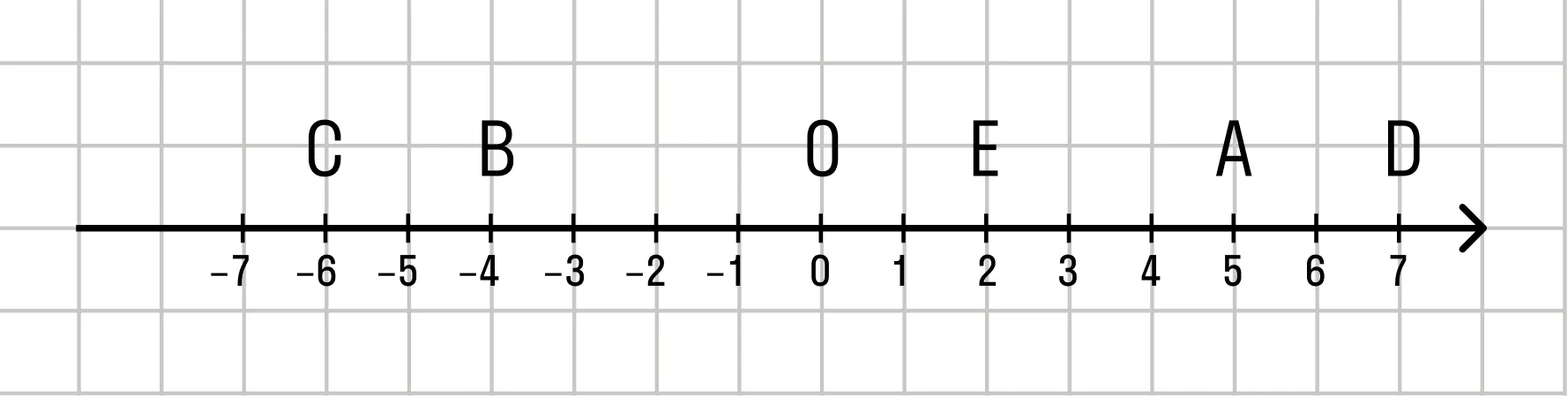
Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

170.4K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Представления действительных чисел

По определению действительными числами являются:

• любое натуральное число;

• любое целое число;

• любая обыкновенная дробь (как положительная, так и отрицательная);

• любое смешанное число;

• любая десятичная дробь (положительная, отрицательная, конечная, бесконечная периодическая, бесконечная непериодическая).

Часто можно встретить действительные числа в виде корней, степеней, логарифмов и др. Кроме того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа.

Также из действительных чисел с помощью арифметических действий, корней, степеней, логарифмических, тригонометрических функций можно составлять числовые выражения, значения которых также будут действительными числами. Например, значения выражений и будут действительными числами.

Сравнение действительных чисел

На множестве действительных чисел справедливы формулы сокращенного умножения и привычные нам законы математики. Например: — это было справедливо на множестве рациональных чисел, но все это справедливо и на множестве действительных чисел.

— все эти законы справедливы на множестве действительных чисел.

Любые действительные числа можно сравнивать. Из двух действительных чисел a и b большим считается то, которое расположено правее на координатной прямой. Для того, чтобы определить, какое число будет правее, можно вычислить их разность.

Число a считается больше числа b, если разность a − b > 0.

Аналогично a меньше b тогда и только тогда, когда разность a − b < 0.

Соответственно:

Примеры: