Угол между прямой и плоскостью — это угол между прямой и её проекцией на эту плоскость.
Например, если прямая
Если угол равен 90°, то проекция прямой является точкой.
Правильный ответ такой: все эти случаи можно озаглавить геометрическим понятием «пересечение плоскости прямой под некоторым углом». Об этом мы сегодня и поговорим, а именно:
рассмотрим главные определения и примеры;
изучим свойства и теоремы по теме;
научимся находить угол между прямой и плоскостью.
Определение угла между прямой и плоскостью
Угол между прямой и плоскостью — это угол между прямой и её проекцией на эту плоскость.
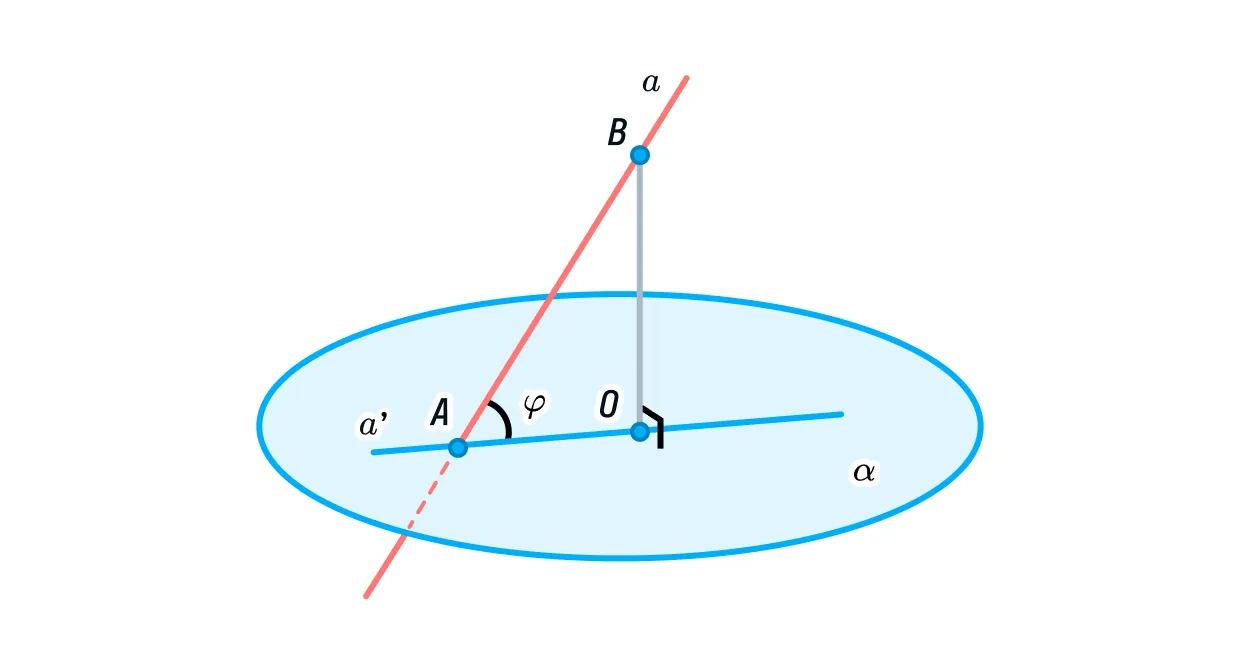
Мы уже знакомы с понятиями «угол», «прямая» и «плоскость» (если подзабыли, то можете повторить по нашим материалам). А сейчас давайте вспомним, что такое проекция.
Проекция — это геометрическое изображение на плоскости, полученное проведением перпендикуляров из всех точек данного тела на плоскость.
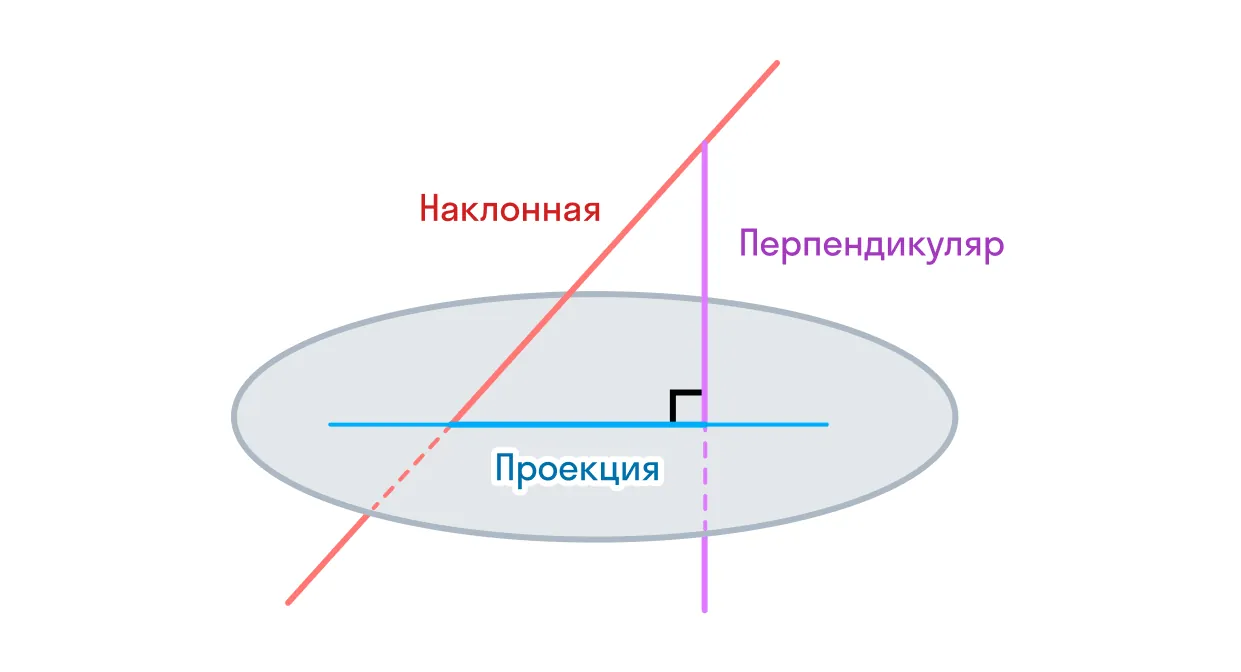
То есть под углом между прямой и плоскостью в пространстве мы подразумеваем угол между прямой и её отображением на плоскость.
Также стоит заметить, что если прямая параллельна плоскости, то у них нет ни одной общей прямой, а значит, угол между ними не определяется.
Как вы думаете, какой тип имеет угол между прямой и плоскостью? Верно, он может быть только острым. Попробуйте доказать это самостоятельно 😊
Свойства и теоремы
Свойство угла между прямой и плоскостью
Углом между прямой и плоскостью называется наименьший из углов между прямой и произвольной прямой в плоскости.
Попробуем привести доказательство. Для этого нарисуем плоскость и проведём к ней прямую АВ, являющуюся наклонной. Тогда АВ1 — проекция прямой на плоскость, АН — произвольная прямая, принадлежащая плоскости, а ВН и ВВ1 — перпендикуляры к плоскости (ВН ⟂ АН, ВВ1 ⟂ АВ). Чтобы лучше представить себе этот объёмный чертеж, можно сделать небольшой макет из сложенного листа бумаги, прислонив его к поверхности стола или тетради.
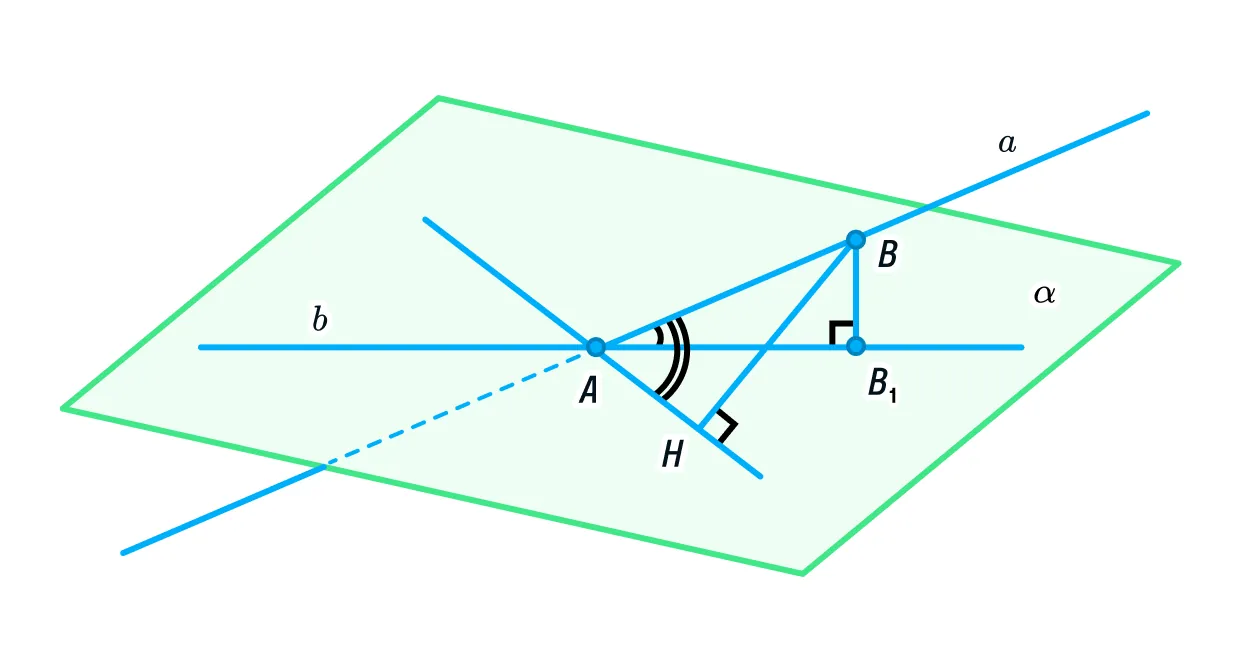
Чтобы проверить истинность свойства, нам необходимо доказать, что угол ∠ВАВ1 намного меньше, чем угол ∠ВАН.
Обозначим проблему: значения этих углов, как и других исходных, нам неизвестны. А значит, на помощь может прийти тригонометрия, ведь сравнить углы можно и через их синусы.
Синус — это отношение противолежащего угла к гипотенузе. В таком случае,
Оба перпендикуляра ВВ1 и ВН проведены из точки В, но только один из них является кратчайшим расстоянием от точки по плоскости, и это перпендикуляр ВВ1. Так как значения синусов представляют собой дроби с одинаковыми знаменателями, большей будет та, у которой больше знаменатель.
Следовательно, sin ∠BAB1 < sin ∠BAH, ∠BAB1 < ∠BAH.
Теорема
Из двух наклонных, проведённых из одной точки к плоскости, меньшая образует с плоскостью больший угол, и наоборот: угол, образованный большей наклонной, будет меньшим из двух.
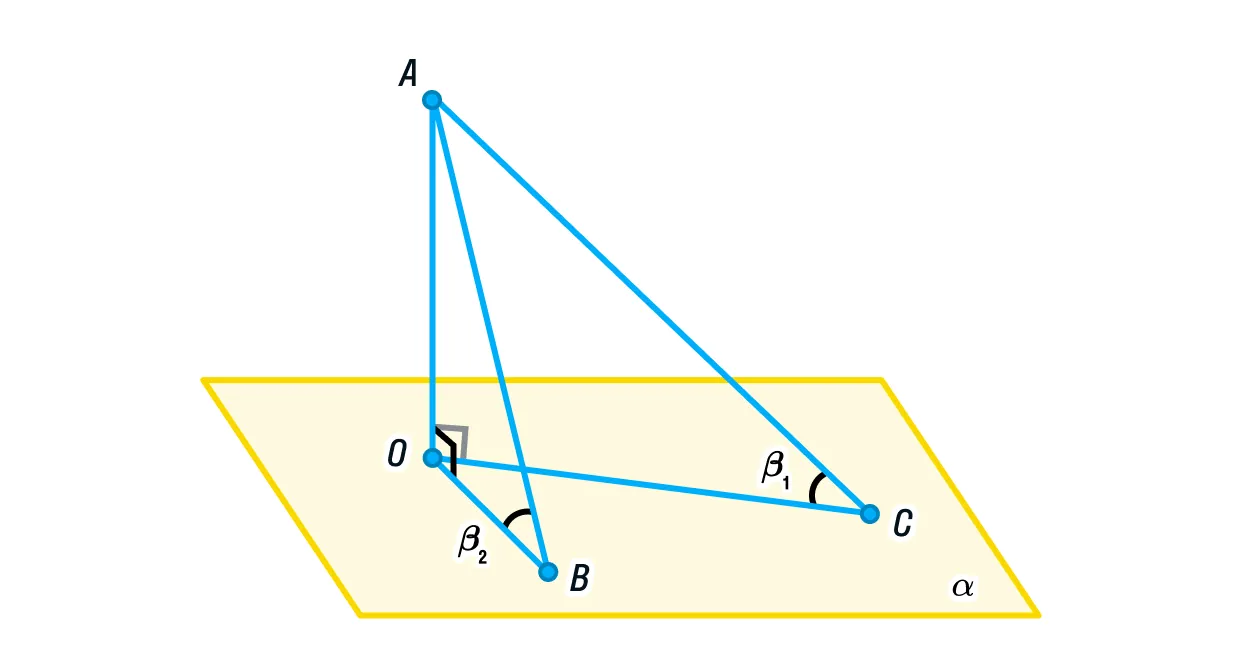
Существует множество разных доказательств этой теоремы, но мы сосредоточимся на одном из них.
Для этого изобразим плоскость и точку
Стороны ОВ и ОС являются проекциями АВ и АС соответственно. Меньшая прямая имеет меньшую проекцию, а значит, ОВ < ОС.
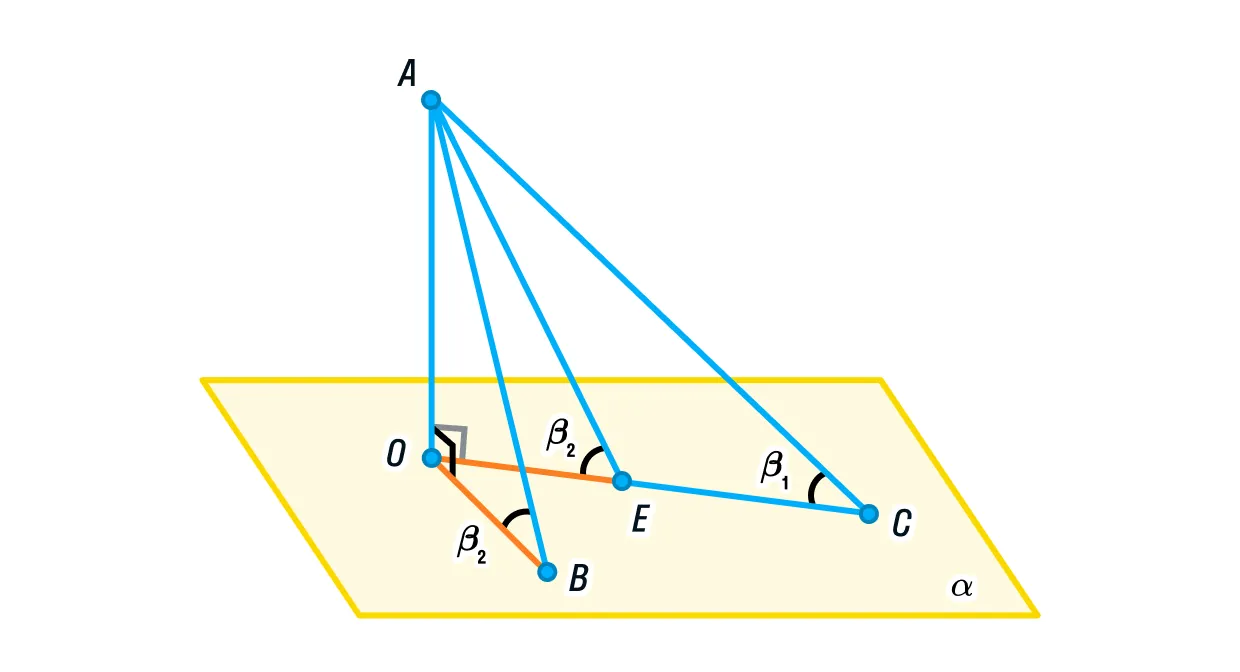
Отложим на стороне ОС отрезок ОЕ, равный ОВ. Можно ли доказать равенство треугольников АОВ и АОЕ?
В данных треугольниках:
ОВ = ОЕ (по построению),
АО — общий катет.
Следовательно, треугольники АОВ и АОЕ равны по двум катетам (или по первому признаку: две стороны и угол между ними). В таком случае равны и соответственные углы: ∠АВО = ∠АЕО.
Угол АЕО является внешним для треугольника АЕС, и по свойству внешнего угла ∠АЕО = ∠АСЕ + ∠САЕ. Не трудно догадаться: раз угол АЕО равен сумме двух других углов треугольника, не смежных с ним, то он больше любого из этих двух углов.
∠АЕО > ∠АСЕ, и так как ∠АЕО = ∠АВО, то ∠АВО > ∠АСЕ.
Что и требовалось доказать. 😎
Получи больше пользы от Skysmart:
-
Подготовься к ОГЭ на пятёрку.
-
Подготовься к ЕГЭ на высокие баллы.
Записывайся на бесплатные курсы для детей.
Решай задания в бесплатном тренажёре ЕГЭ.
Как найти угол между прямой и плоскостью
От теории переходим к практике: а как же можно вычислить угол между прямой и плоскостью? Вопрос лёгкий и сложный одновременно. Дело в том, что задач на нахождение угла очень много, и в каждой из них применяется свой алгоритм решения. Большую роль играет предмет и раздел, в котором эта задача приведена: это может быть стереометрия, векторная алгебра и даже физика. Но все эти алгоритмы сводятся к двум методам: геометрическому и алгебраическому или координатному методу. Давайте подробно рассмотрим каждый из них.
Геометрический метод
Чтобы применить геометрический метод, необходимо опустить перпендикуляр на плоскость из точки, принадлежащей исходной прямой. Выясним, чем в этом задании является перпендикуляр, наклонная и проекция, и решим планиметрическую задачку (чаще всего в таких задачах нам будет необходимо найти один из углов прямоугольного треугольника).
Задача 1
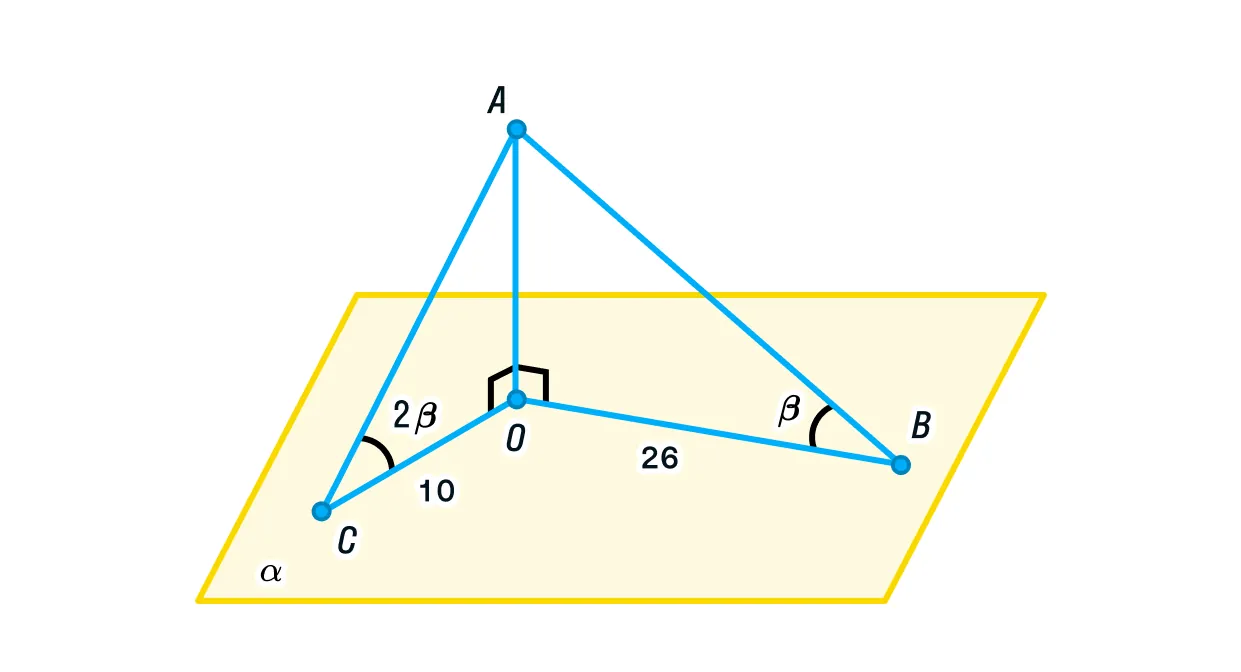
Из точки А на плоскость проведены две наклонные АВ и АС и перпендикуляр АО, причём О, В и С — точки пересечения с плоскостью
Определите, чему равен АО, если СО = 10, ВО = 26, а угол АСО в два раза больше угла АВО.
Решение:
Отметим на стороне ОВ отрезок, равный ОС. Тогда ОС = ОЕ = 10, а ЕВ = 26 – 10 = 16.
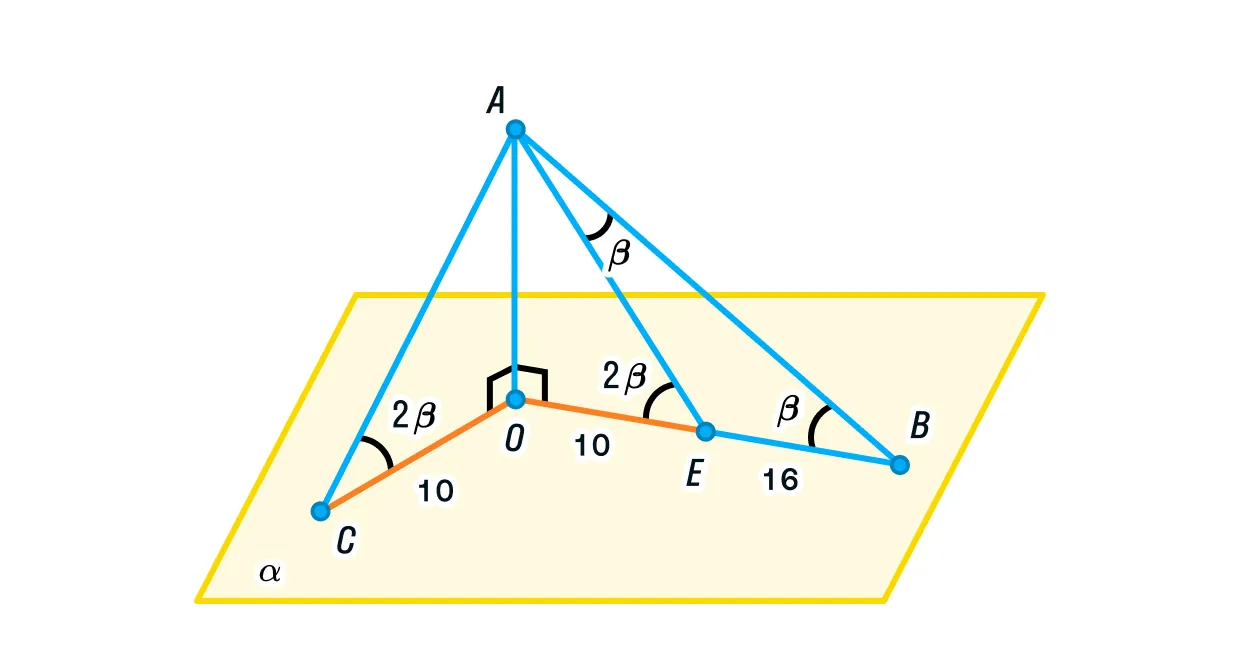
Рассмотрим треугольники АСО и АЕО:
СО = ОЕ (по построению),
АО — общий катет.
Следовательно, треугольники равны по двум катетам. А значит, угол АСО равен углу АЕО.
Угол АЕО является внешним для треугольника АЕВ, а значит, ∠АЕО = ∠АВЕ + ∠ВАЕ. Так как ∠ АВЕ = , значит, ∠ ВАЕ = 2-=, и треугольник АЕВ — равнобедренный.
Тогда найдём АО через прямоугольный треугольник АОЕ по теореме Пифагора:
Ответ:
Алгебраический метод
Алгебраический метод или метод координат для нахождения угла между прямой и плоскостью основывается на особой формуле. Чтобы использовать его, необходимо определить координаты двух точек, принадлежащих прямой, описать уравнение плоскости и применить формулу. По сути в этом методе мы находим угол между вектором и плоскостью.
где (x1, y1, z1) — это координаты первой точки,
(x2, y2, z2) — координаты второй точки,
А, В и С — это координаты в уравнении плоскости Ax + By + Cz + D = 0.
Иначе эти числа называют координатами вектора нормали плоскости.
Тут может возникнуть вопрос: а что, если в задаче даны не координаты точек, а координаты вектора?
В этом случае вспомним, что координаты вектора находятся через разность координат начала и конца. А значит, мы со спокойно душой подставляем эти координаты в формулу вместо (х2 – х1), (y2 – y1) и (z2 – z1).
В некоторых задачах для нахождения угла между прямой и плоскостью вводят понятие направляющего вектора прямой. Направляющий вектор прямой — это любой вектор, не равный нулю, который размещается на данной прямой или же на прямой, параллельной ей.
Координаты этого вектора можно получить из канонического уравнения прямой:
Тогда угол между прямой и плоскостью можно вычислить по формуле:
Задача 2
Найдите угол между прямой
Решение:
Определим координаты направляющего вектора для прямой: (2; –1; 3).
Определим координаты вектора нормали плоскости: (3; –1; –1).
Подставим координаты в формулу для расчёта синуса угла между плоскостью и прямой:
Задача 3
Найдите угол между плоскостью, заданной уравнением x + 2y + 2z – 4 = 0, и прямой, которой принадлежат точки А (0, 2, –1) и В (–2, 4, –1).
Решение:
Определим координаты вектора нормали плоскости: (1; 2; 2).
Подставим координаты вектора нормали и координаты точек прямой в формулу:
За короткий промежуток времени мы изучили понятие угла между прямой и плоскостью, доказали теоремы, разобрали способы нахождения угла и решили практические задания. Мы — молодцы! 💪
Думаем, вы понимаете, что эта тема очень важна — с её помощью решаются сложные стереометрические задачи, которые встречаются на ОГЭ и ЕГЭ. Подготовиться к таким серьёзным заданиям помогут курсы профильной математики в онлайн-школе Skysmart. На уроках мы сможем более подробно разобрать задачи с пирамидами и параллелепипедами, а ещё научимся составлять уравнения для любой плоскости. Узнать свои сильные и слабые стороны, составить план обучения и познакомиться с онлайн-платформой можно на вводном уроке — это бесплатно.
