Определение противоположных чисел
В 6 классе каждый школьник должен узнать, какие числа являются противоположными. Сейчас расскажем! Для начала построим координатную прямую.
Координатная ось — это прямая линия, на которой отмечено начало координат, задан единичный отрезок и стрелкой указано положительное направление.
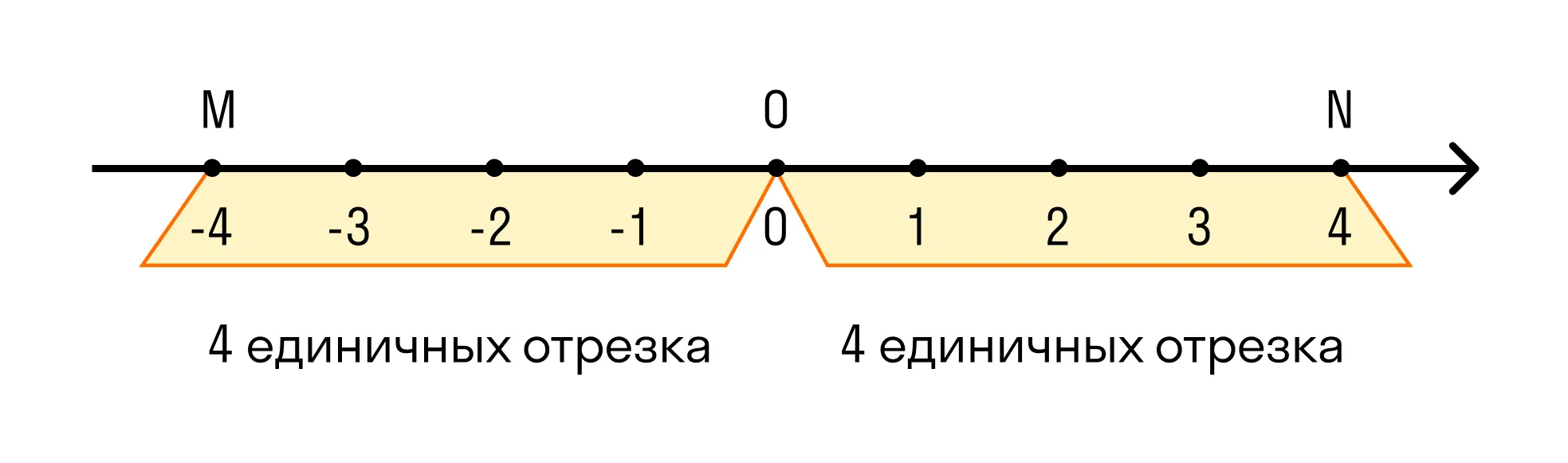
Точки M(-4) и N(4) одинаково удалены от точки O и находятся в противоположных направлениях по разные стороны от нее. Поэтому числа -4 и 4 называют противоположными.
Противоположными называются числа, которым соответствуют такие точки на координатной прямой, в которые мы попадем, если отметим одно и то же расстояние от начала отсчета в разных направлениях (положительном и отрицательном). Нуль при этом находится в начале отсчета и противоположен сам себе.
Пары противоположных чисел:
- 1 и -1;
- 0,25 и -0,25;
- 88,158 и -88,158;
- 2/7 и -2/7.
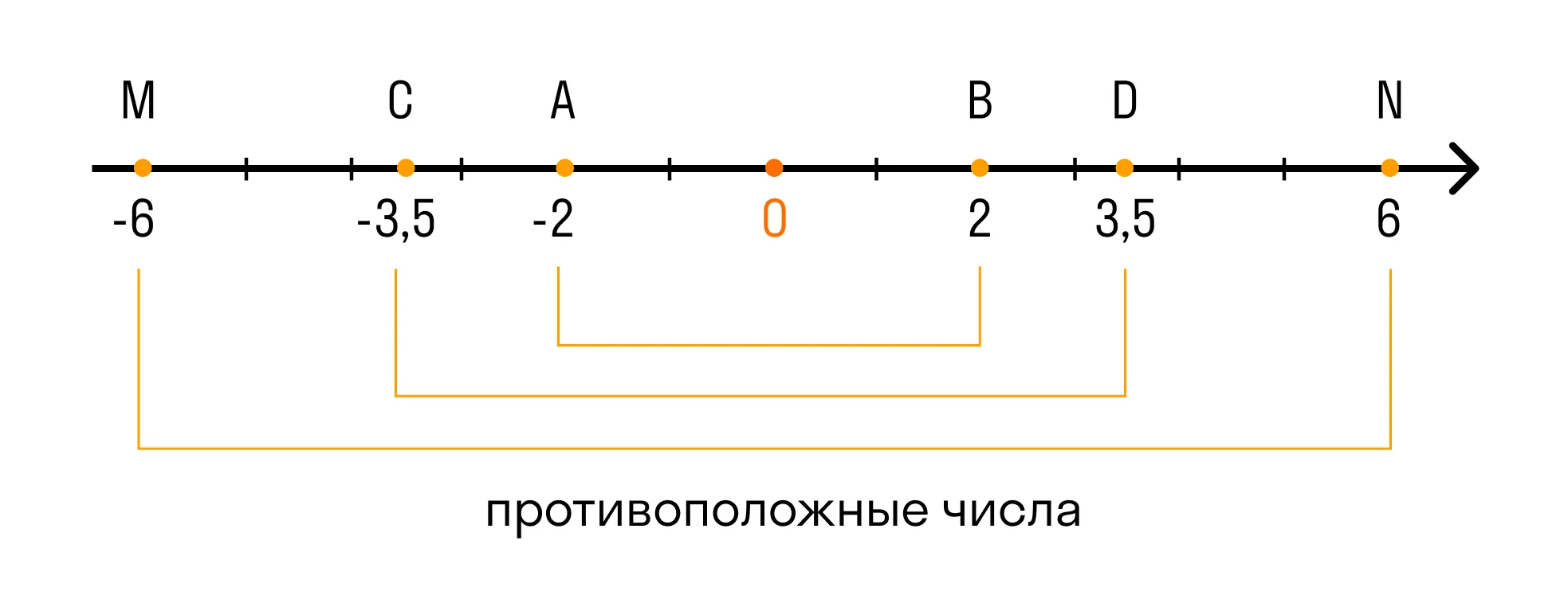
Целые числа включают в себя натуральные числа, числа противоположные натуральным (то есть с отрицательным знаком) и ноль.
Обозначение противоположных чисел
У противоположных чисел есть основные обозначения. Если нам дано число и нужно записать противоположное ему, то для этого нужно использовать знак минус: «-».
Противоположные числа — это два числа, которые отличаются друг от друга знаками.
Другими словами, число, которое противоположно t, обозначается -t. Например:
- Если t = -13, то ему противоположное -t = 13.
- Если t = 0,123, то ему противоположное -t = -0,123.
- Если t = 0, то ему противоположное -t = 0.
Запись -(-t) означает число, противоположное -t. Например, -(-0,09) = 0,09. Число, противоположное -0,09, есть число 0,09.
Примеры противоположных чисел:
- -1809 и 1809;
- √202 и -√202;
- -20 и -(-20).
Примеры противоположных рациональных чисел:
- 1,121 и -1,121;
- 0,(5678) и -0,(5678).
Противоположными могут быть и иррациональные числа, например, значения числовых выражений (√4 + 2) и -(√4 + 2).
Получи больше пользы от Skysmart:
-
Прокачивай знания на курсах математики.
-
Выбирай из 1200+ репетиторов по математике.
Записывайся на бесплатные курсы для детей.
Свойства противоположных чисел
Перечислим основные свойства противоположных чисел:
- Для каждого действительного числа существует только одно число, которое ему противоположно.
Это объясняется тем, что для каждой точки координатной оси существует только одна точка, симметричная ей относительно нуля.
- Противоположные числа имеют разные знаки: одно из них является положительным, а второе отрицательным.
Это свойство следует из того, что противоположные числа находятся на координатной оси по разные стороны от нуля и имеют разные знаки. Исключение: число нуль (0).
Значит, если исходное число со знаком плюс, то противоположное ему будет со знаком минус. А если исходное число является отрицательным, то противоположное ему будет положительным.
- Свойство симметричности: если число a противоположно числу b , то b противоположно a .
- Модули противоположных чисел равны.
Точки координатной прямой, которые соответствуют противоположным числам, находятся на одинаковом расстоянии от начала отсчета.
- Сумма противоположных чисел всегда равна нулю:
n + (-n) = n - n = 0.
То есть, такие числа одинаковы по модулю, но имеют разные знаки.
Рассмотрим несколько примеров. Сумма противоположных чисел 101 и -101 равна 0, результат сложения противоположных чисел √5 и -√5 также равен нулю.
Задания для самопроверки
Назовите число, противоположное данному:
- 20 472;
- −15;
- −0,3;
- √1048;
- 0.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
