Для кого эта статья:
- Ученики, готовящиеся к ЕГЭ по математике
- Преподаватели математики, ищущие материалы для подготовки
- Родители, желающие помочь детям в подготовке к экзаменам
Теорема Пифагора
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии. Она устанавливает соотношение между сторонами прямоугольного треугольника. И звучит так:
В прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы.
c2 = a2 + b2.
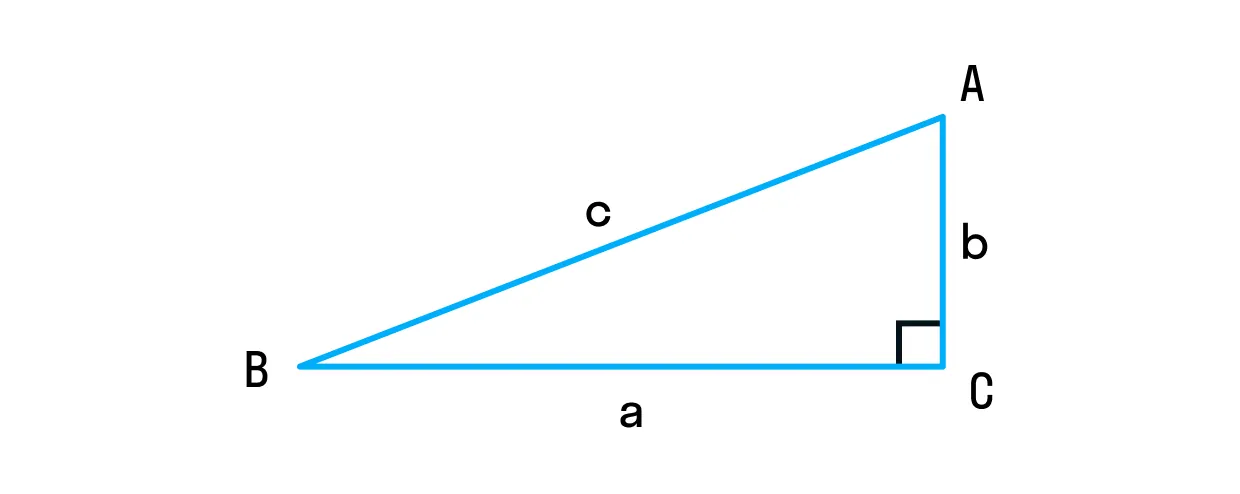
Теорема Пифагора — это частный случай теоремы косинусов. Это объясняется тем, что косинус 90 градусов равен нулю.

Теорема Фалеса
Теорема Фалеса — это свойство параллельных прямых, которые пересекают две секущие с общей точкой.
Вообще, есть две теоремы Фалеса — общая, на все случаи жизни, и частная — то, что нужно для решения задач на ЕГЭ по математике.
Через произвольные точки A1, A2, … An–1, An, лежащие на стороне AO угла AOB, проведены параллельные прямые, пересекающие сторону угла OB в точках B1, B2, … Bn–1, Bn, соответственно. Тогда справедливы равенства:
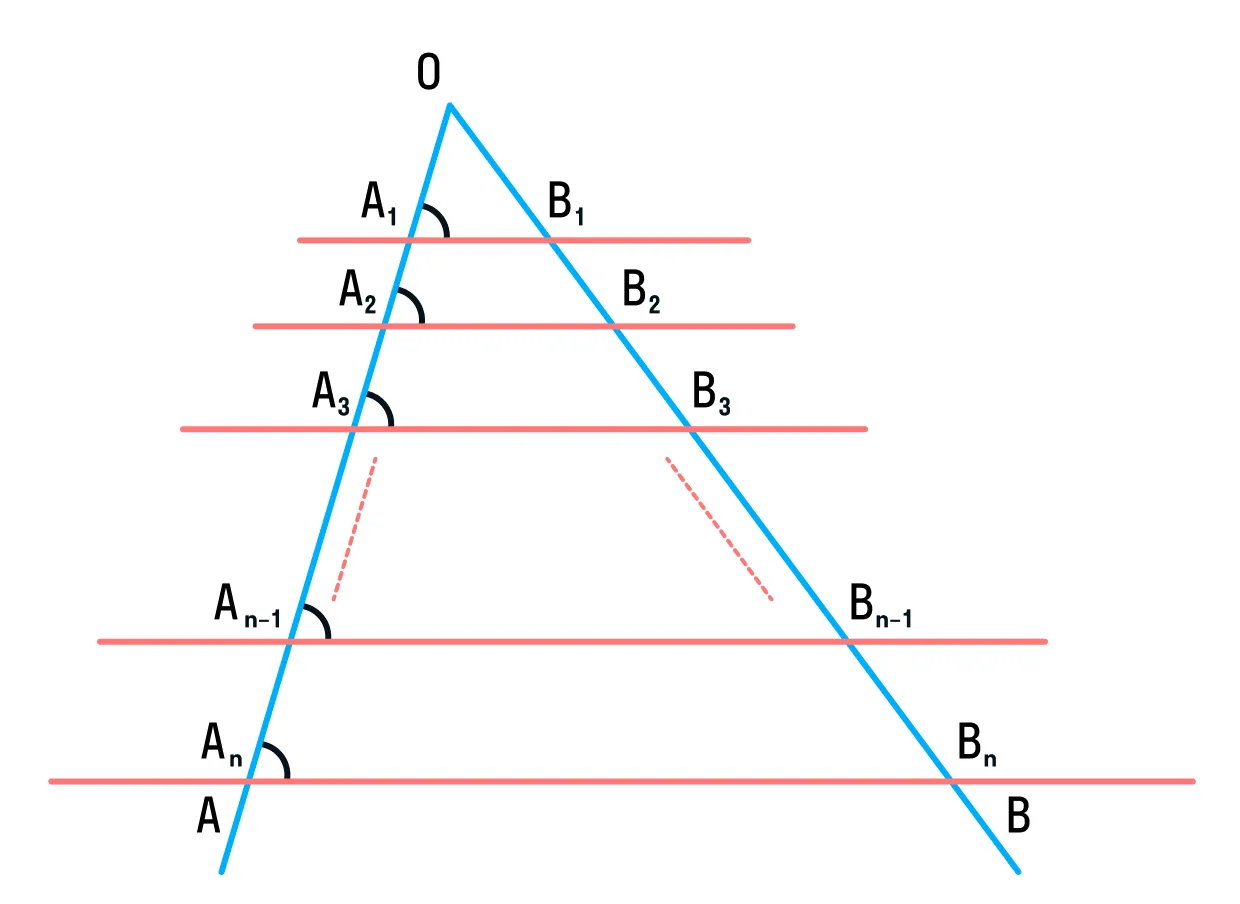
В ЕГЭ по математике теорема Фалеса встречается чаще всего в параллелограмме, у которого проведена диагональ, — будьте начеку.
Получи больше пользы от Skysmart:
-
Подготовься к ОГЭ на пятёрку
-
Подготовься к ЕГЭ на высокие баллы
Записывайся на бесплатные курсы для детей
Решай задания в бесплатном тренажёре ЕГЭ
Теорема косинусов
Теорема Пифагора — кайф, легко запомнить, часто встречается, применяем только тогда, когда у нас есть прямоугольный треугольник. Но на самом деле теорема Пифагора работает для любого треугольника, только называется она в этом случае теоремой косинусов.
Квадрат длины стороны треугольника равен сумме квадратов длин других сторон минус удвоенное произведение длин этих сторон на косинус угла между ними.
a2 = b2 + c2 – 2bc cos A
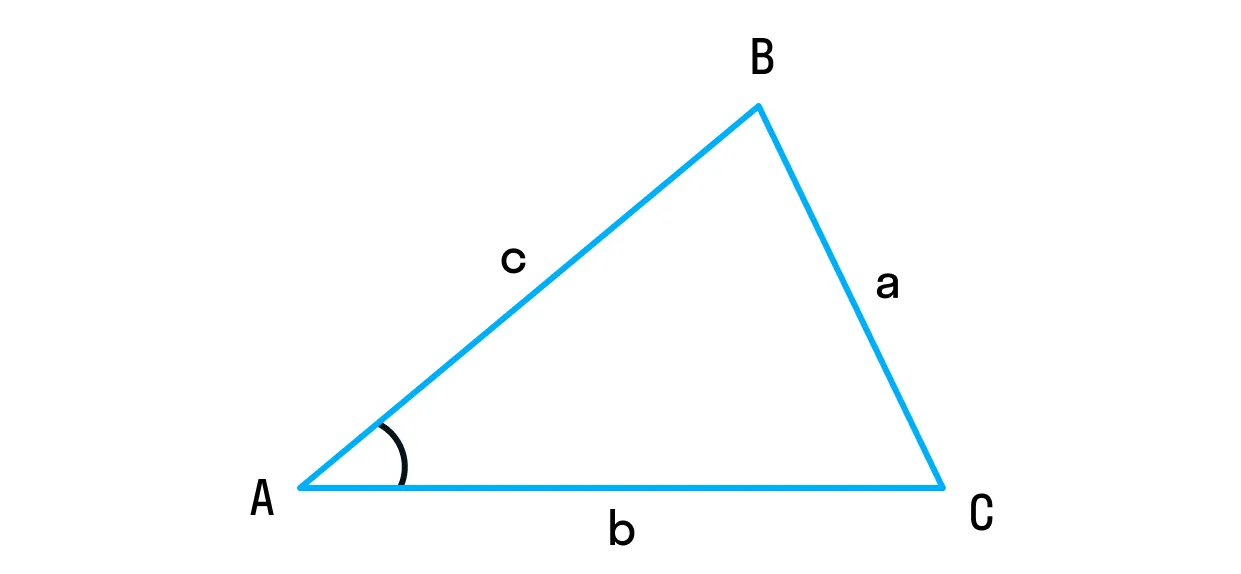
Собственно, по формуле сразу становится понятно, почему это соотношение называется теоремой косинусов. Ещё она крайне похожа на разность квадратов с учётом косинуса, поэтому запомнить её не очень сложно. И если вспомнить, что косинус 90 градусов — это 0, то мы увидим знакомую теорему Пифагора.
Теорема синусов
Казалось бы, синус — это что-то про тригонометрию, но на самом деле совсем не только. Планиметрия может с этим смело поспорить, и теорема синусов — явный аргумент в этом воображаемом споре. Если коротко, теорема синусов — это формула связи угла с противолежащей ему стороной в треугольнике.
Для любого треугольника справедливы равенства:
где R — радиус описанной около треугольника окружности.
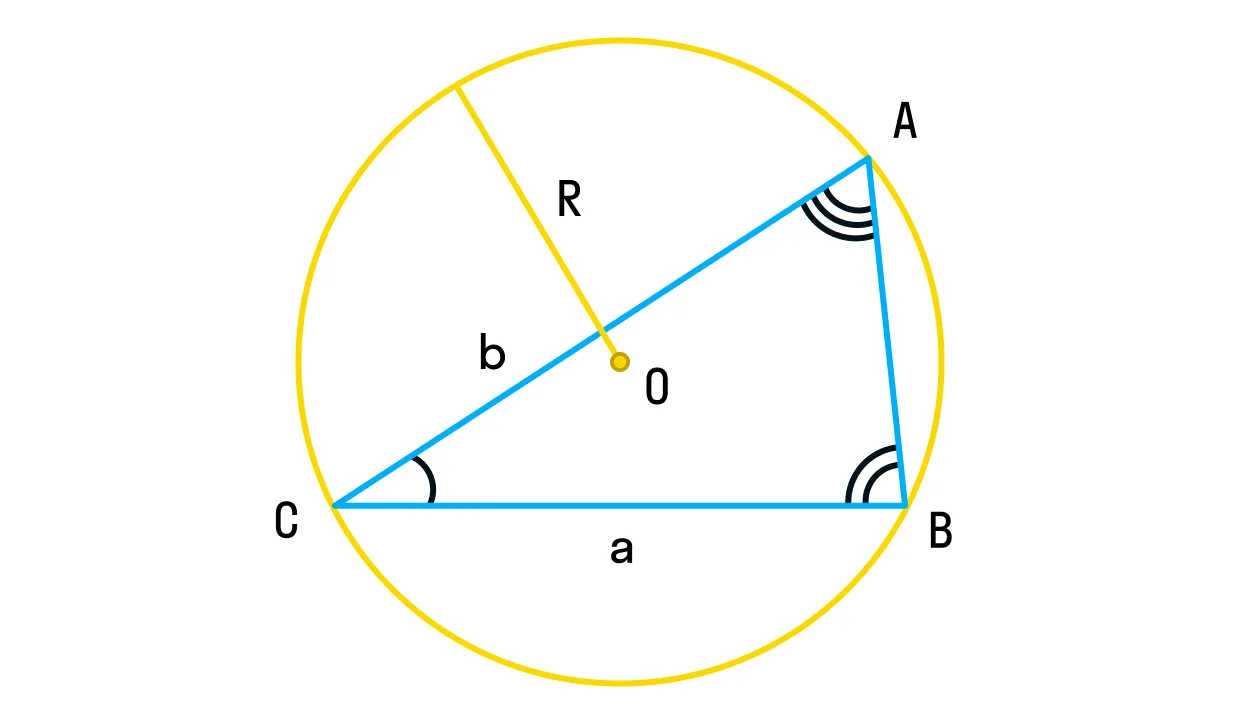
По теореме синусов, во-первых, можно быстро найти радиус описанной окружности по известной стороне и противолежащему ей углу. Во-вторых, если треугольник не прямоугольный, то в нём можно просто найти синус угла по известным стороне и радиусу описанной окружности. Ну и в конце концов, можно использовать отношение двух любых сторон и углов. Формула синусов в ЕГЭ по математике используется нечасто, но иметь её в своем арсенале полезно и обязательно.
Теорема Менелая
Её также называют теоремой о треугольнике и секущей, и звучит она так:
Если на сторонах AB и BC треугольника ABC взяты соответственно точки C1 и A1, а точка B1 взята на продолжении стороны AC за точку C, то точки C1, A1 и B1 лежат на одной прямой тогда и только тогда, когда выполнено равенство:
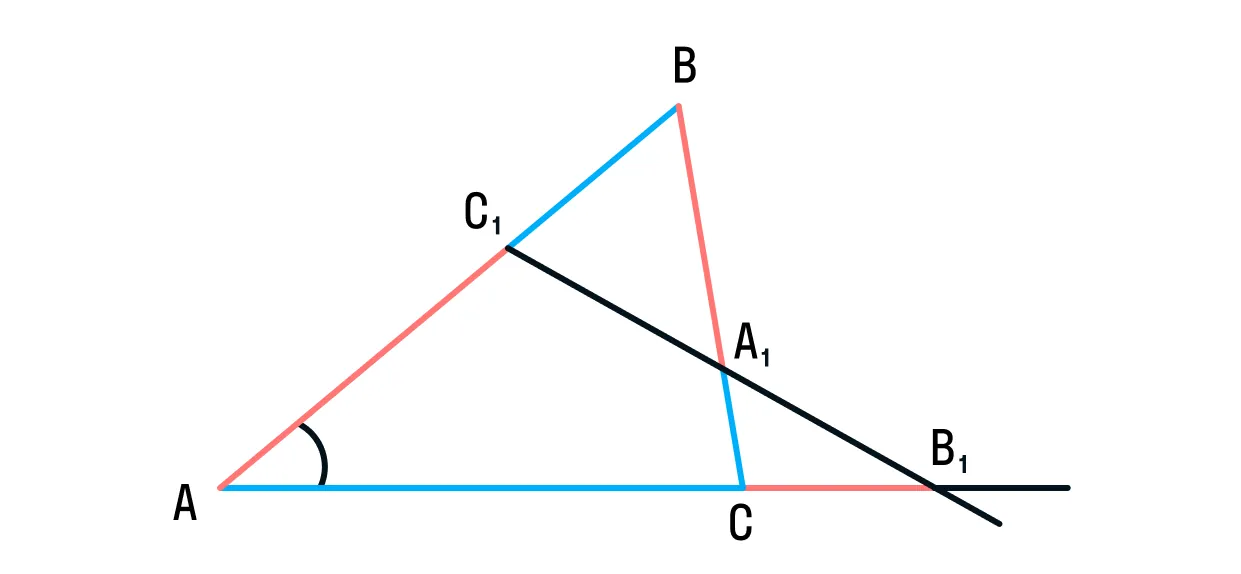
Теорема Менелая пригодится для решения 2-й части ЕГЭ по математике. Она поможет уменьшить огромную кучу исписанных листочков при решении и сохранить время на экзамене, ведь помогает решать в несколько действий.
Чтобы с лёгкостью запомнить все основные теоремы из геометрии для ЕГЭ по математике, скачайте и распечатайте удобную шпаргалку. Кроме теорем из этой статьи, там есть ещё две редкие — теоремы Чевы и Вариньона, а также задачи на доказательства.
Математика — обязательный для сдачи на ЕГЭ предмет, без которого не получишь аттестат. Это также один из самых сложных экзаменов для выпускников. Делимся типичными ошибками в ЕГЭ по математике, а также ресурсами, которые помогут отработать теорию на практике.





















