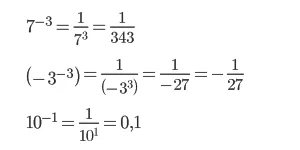Онлайн-калькулятор степеней
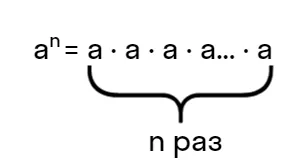
Степенью n числа а является произведение множителей величиной а n раз подряд. an — степень, где: a — основание степени, n — показатель степени.
Результат:
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
- an — степень,
где:
a — основание степени;
n — показатель степени.
Соответственно:
Читается такое выражение, как a в степени n
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
- 23 = 2·2·2, где:
2 — основание степени;
3 — показатель степени.
Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.
Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.
Задачка про миллион: представьте, что у вас есть миллион рублей. За один год вы заработали на нем еще два. Еще через год каждый миллион принес еще два и т. д. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.
Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:
- 3·3·3·3 = 81. То есть получается, что три в степени четыре равно 81.
Математики заскучали и решили все упростить:
- 34 = 81
Ответ: через четыре года у вас будет 81 миллион.
Получи больше пользы от Skysmart:
-
Прокачивай знания на курсах математики
-
Выбирай из 1200+ репетиторов по математике
Записывайся на бесплатные курсы для детей
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени 2) и куб (показатель степени 3).
|
Число |
Вторая степень |
Третья степень |
|
1 |
1 |
1 |
|
2 |
4 |
8 |
|
3 |
9 |
27 |
|
4 |
16 |
64 |
|
5 |
25 |
125 |
|
6 |
36 |
216 |
|
7 |
49 |
343 |
|
8 |
64 |
512 |
|
9 |
81 |
729 |
|
10 |
100 |
1000 |
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Свойства степеней
В математике степень с натуральным показателем имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук — ниже мы их рассмотрим.
Мы будем употреблять такие понятия, как натуральные числа, целые числа, рациональные числа, иррациональные числа. Чтобы не запутаться, дадим им определение:
- Натуральные числа — это числа, которые мы используем, чтобы считать предметы: один банан, два банана.
- Целые числа — это все натуральные числа, все противоположные натуральным числам и число 0.
- Рациональными называют числа, которые можно представить в виде обыкновенной дроби. Например: 1/2; −5/3; 8/4.
- Иррациональные числа — это бесконечная десятичная дробь. Например, число пи как раз такое — 3,141592…
Все, теперь мы точно готовы разбираться со свойствами степеней. Поехали!
Свойство 1: произведение степеней
При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:
an · am = am+n
a — основание степени
m, n — показатели степени, любые натуральные числа.
Свойство 2: частное степеней
Когда мы делим степени с одинаковыми основаниями, основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n
Свойство 3: возведение степени в степень
Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.
(an)m = an· m
a — основание степени
m, n — показатели степени, натуральное число
Свойство 4: возведение в степень произведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
(a · b)n = an · bn
a, b — основание степени
n — показатели степени, натуральное число
Свойство 5: возведение в степень частного
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a : b)n = an : bn
a, b — основание степени, b ≠ 0,
n — показатель степени, натуральное число
Сложение и вычитание степеней
Как складывать числа со степенями и как вычитать степени — очень просто. Основной принцип такой: выполняется сначала возведение в степень, а уже потом действия сложения и вычитания.
23+ 34= 8 + 81= 89
63- 33= 216 - 27 = 189
|
И еще парочка правил
|
Давай потренируемся
Реши примеры со степенями:
-
23 + 24 =
-
34 + 54 =
-
63 − 33 =
-
74 − 32 =
В конце статьи ты найдешь правильные ответы.
Примеры умножения и деления степеней
Умножение степеней с одинаковыми показателями
Чтобы произвести умножение степеней с одинаковыми показателями, можно перемножить основания и возвести произведение в степень, показатель которой останется прежним:
- an · bn = (a · b)n , где
a, b — основание степени (не равное нулю)
n — показатели степени, натуральное число
- a5 · b5 = (a·a·a·a·a) ·(b·b·b·b·b) = (ab)·(ab)·(ab)·(ab)·(ab) = (ab)5
- 35 · 45 = (3·4)5 = 125 = 248 832
- 16a2 = 42·a2 = (4a)2
Умножение степеней с одинаковыми основаниями
Степени с одинаковыми основаниями умножаются путём сложения показателей степеней:
am · an= am+n, где
a — основание степени
m, n — показатели степени, любые натуральные числа
- 35 · 32 = 35 + 2 = 37 = 2 187
- 28 · 81= 28 · 23 = 28 + 3 = 211 = 2048
Умножение степеней с разными основаниями и показателями
Если разные и показатели, и основания, и одна из степеней не преобразуется в число с тем же основанием, как у другой степени (как здесь: 28 · 81= 28 · 23 = 211 = 2048), то производим возведение в степень каждого числа и лишь затем умножаем:
- 33 · 52 = 27·25 = 675
Деление степеней с одинаковыми основаниями и одинаковыми показателями
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n

Деление чисел с одинаковыми показателями степени
При делении степеней с одинаковыми показателями результат частного этих чисел возводится в степень:
- an : bn = (a : b)n , где
a, b — основание степени, b ≠ 0,
n — показатель степени, натуральное число
Пример:
53 : 23 = (5 : 2)3 = 2,53 = 15,625
Деление степеней с разными основаниями и показателями
Если разные и показатели, и основания, то возводим в степень каждое число и только потом делим:
- 33 ÷52 = 27÷25 = 1,08
Степень с отрицательным показателем и её свойства
Число с отрицательным показателем степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
|
Примеры
|
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
- a3÷a6=a3 - 6 = a-3
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Умножение отрицательных степеней
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:
am · an = am+n
|
Примеры |
Деление отрицательных степеней
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:
|
Примеры 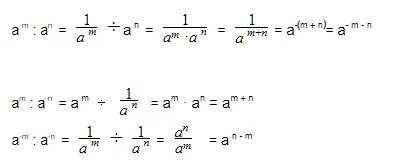 |
Возведение дроби в отрицательную степень
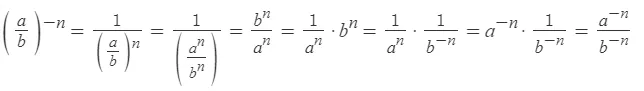
Возведение произведения в отрицательную степень
Как представить число в виде степени
Чтобы представить число в виде степени, нужно разложить его на простые множители. Если в произведении встречаются несколько одинаковых сомножителей, то это произведение записывается в виде степени.
Например, представим в виде степени число 243:
243 = 3 × 3 × 3 × 3 × 3 = 35
Ответы на вопросы для самопроверки
-
24
-
706
-
189
-
2392