Порядок действий в математике

Основные операции в математике

Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).

Операции действия:

• сложение (+);

• вычитание (-);

• умножение (*);

• деление (:).

Операции отношения:

• равно (=);

• больше (>);

• меньше (<);

• больше или равно (≥);

• меньше или равно (≤);

• не равно (≠).

Пройдите тест и узнайте, какие темы отделяют от пятёрки по математике

Привет! Это Макс, он хочет отпраздновать начало учебного года. Давай поможем Максу подготовиться к празднику

Жми на стрелки сверху, чтобы путешествовать в истории →

‌

Макс делал домашку и потерял счёт времени. Он забыл, что Саша и Чак совсем скоро придут в гости →

‌

Посчитай, сколько времени нужно Максу на все дела

Максу понадобится 13 12 14 15 минут, чтобы все успеть

‌

Первое дело уже в работе! Для торта Максу в магазине нужно докупить продукты→

‌

Максу надо докупить мармелад, сгущёнку и яйца

Cколько рублей надо заплатить Максу?

Ответ: 23 рубля 24 рубля 21 рубль 22 рубля

Макс купил муку, яйца, масло, сгущёнку и мармелад. Начинаем готовить торт! →

Рассчитай, сколько весят ингридиенты для торта

4 * 50 = 250 200 220 230 грамм весят 4 яйца

142 + 150 + 137 = 429 432 427 426 грамм весят 3 яблока

6 * 7 = 44 46 42 48 грамма весит полстакана сахара

32 : 4 = 6 4 8 10 столовых ложек муки в стакане

В домофон звонят Саша и Чак, а Макс забыл прибраться! У вас всего несколько минут

‌

Макс уберёт книги перед тем, как пропылесосить, а посуду помоет после того, как пропылесосит. В каком порядке Макс сделает дела?

2 1 3

Супер! Благодаря тебе Макс сделал все дела.

Дальше узнаешь свои результаты →

‌

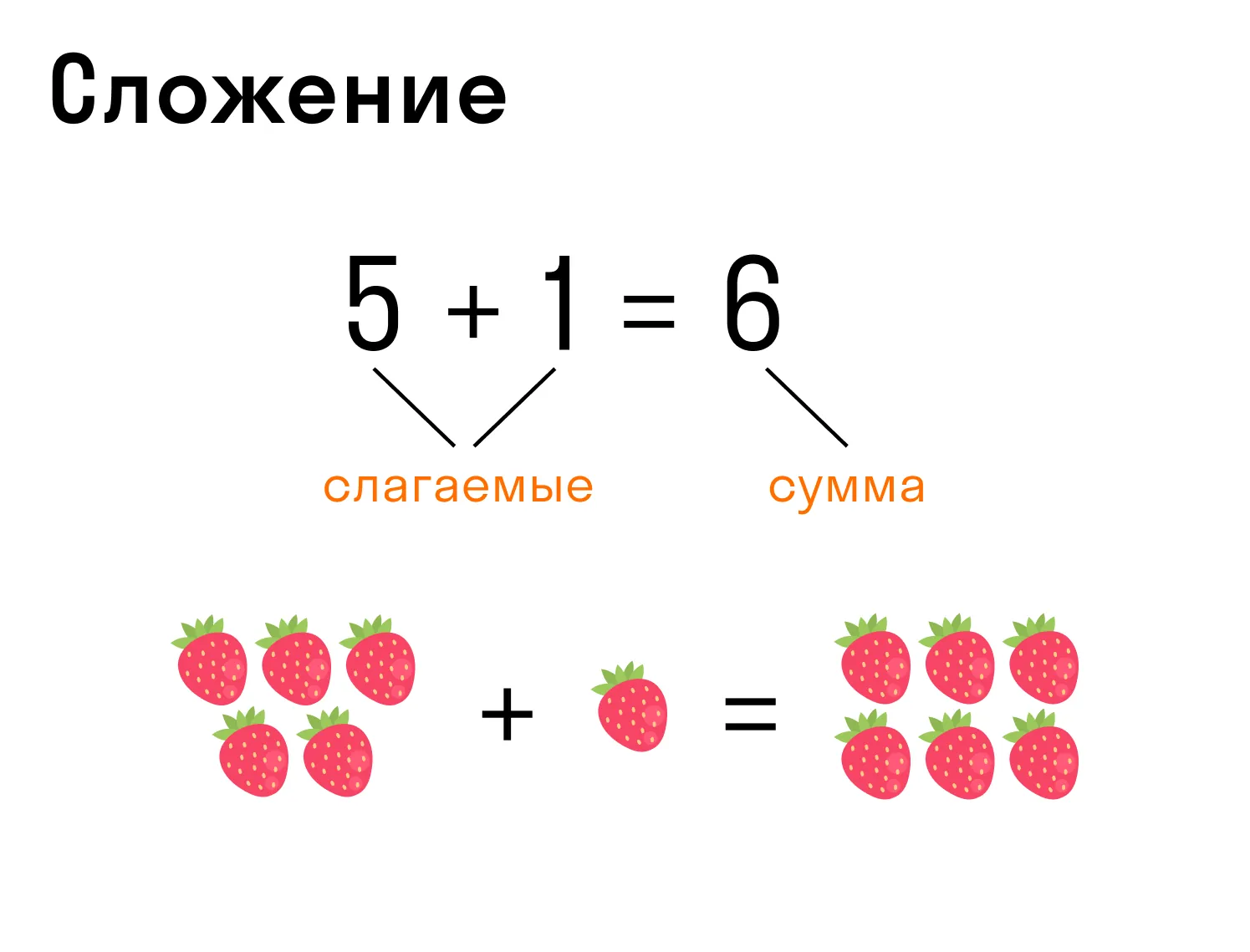
Сложение — операция, которая позволяет объединить два слагаемых.

• Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.

Вычитание — действие, обратное сложению.

• Запись вычитания: 10 - 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

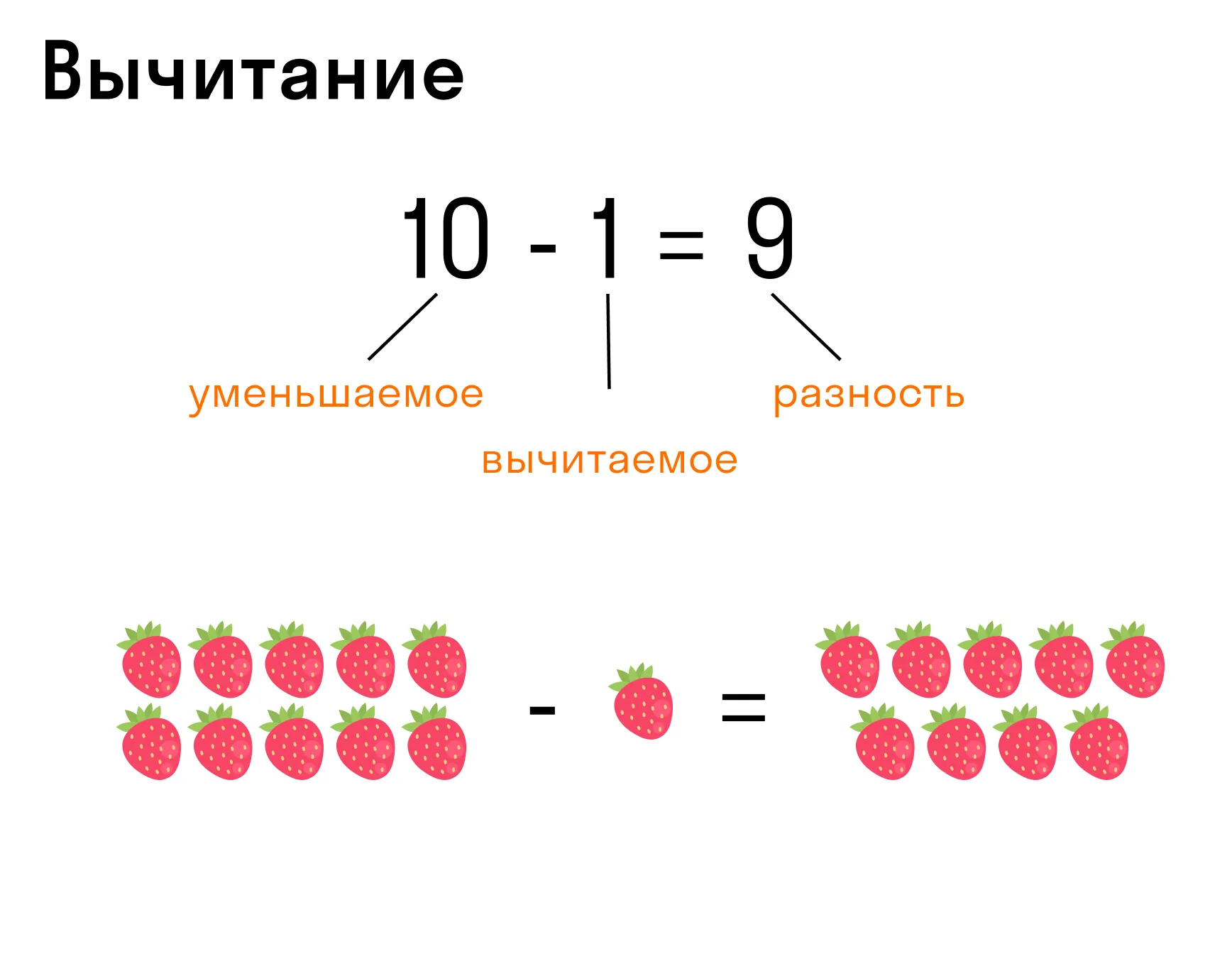
Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 - 1 = 9.

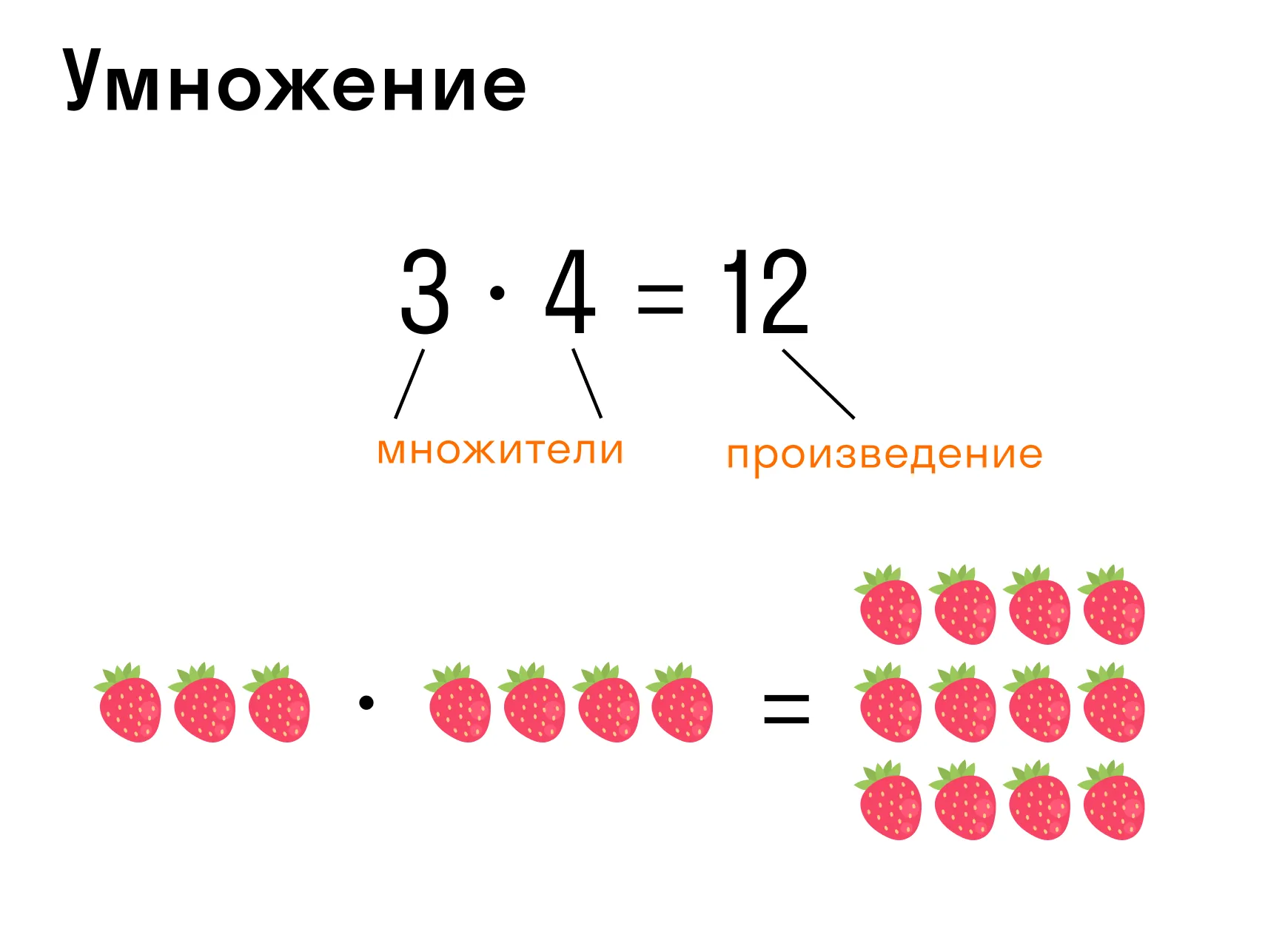
Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

• Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.

  

• 3 × 4 = 3 + 3 + 3 + 3, то есть число 3 сложили 4 раза само с собой.

  

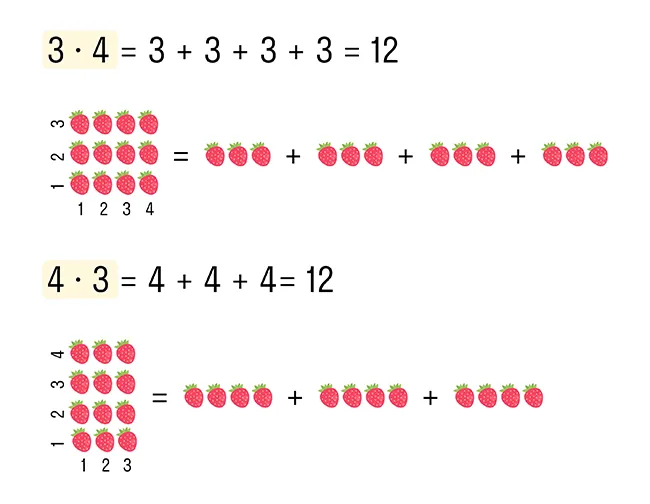
В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 × 2 = 5 + 5 = 10 и 2 × 5 = 2 + 2 + 2 + 2 + 2 = 10.

Поэтому и множитель, и множимое называют сомножителями.

Деление — арифметическое действие обратное умножению.

• Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.

  

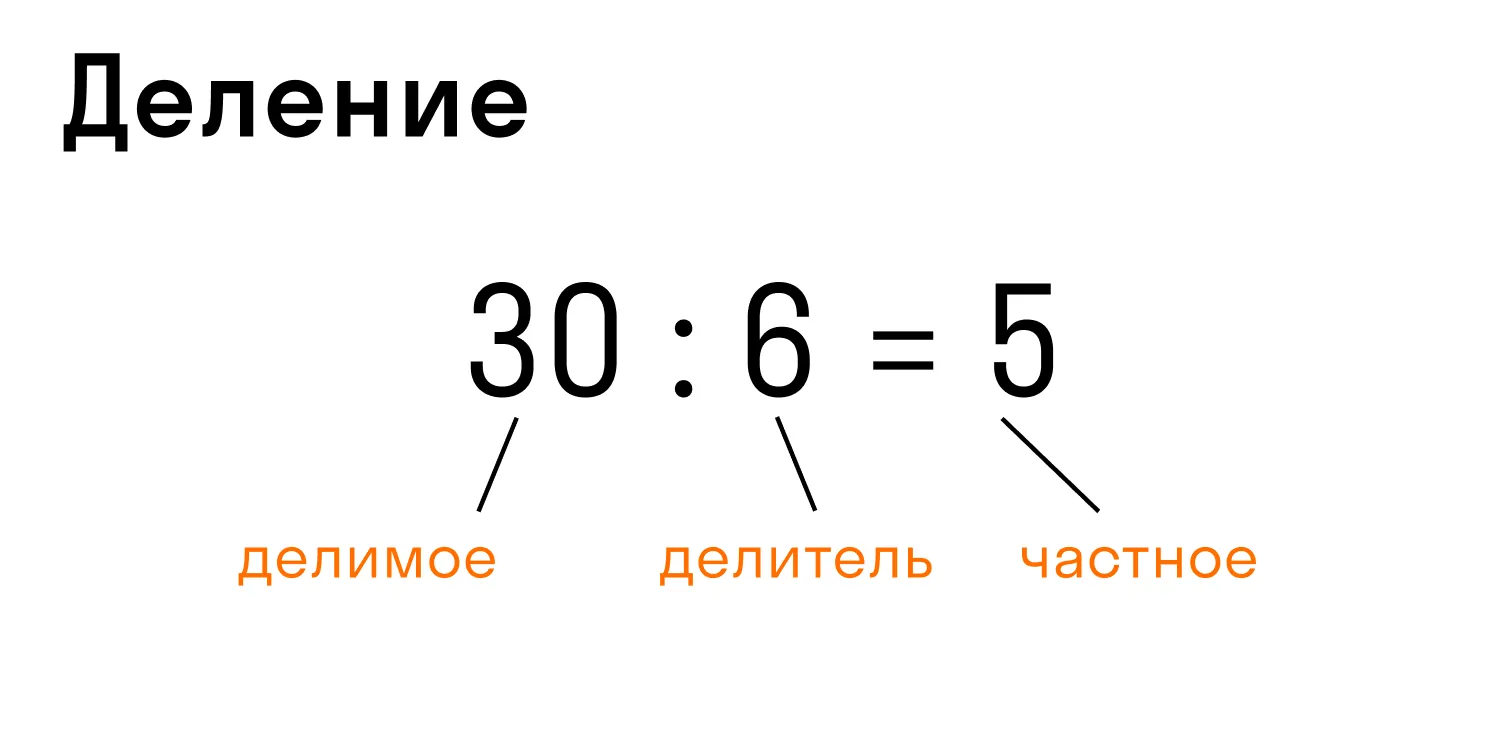
В этом случае произведение делителя 6 и частного 5 в качестве проверки дает делимое 30.

Сложение и вычитание, умножение и деление попарно представляют обратные друг другу действия. А теперь давайте узнаем порядок выполнения арифметических действий.

 

Порядок вычисления простых выражений

Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:

• действия выполняются по порядку слева направо

• сначала выполняется умножение и деление, а затем — сложение и вычитание.

Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.

Что первое, умножение или деление? — По порядку слева направо. Сначала умножение или сложение? — Умножаем, потом складываем.

Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Рассмотрим порядок арифметических действий в примерах.

Пример 1. Выполнить вычисление: 11 − 2 + 5.

Как решаем:

В нашем выражении нет умножения, деления и скобок, поэтому выполняем все действия слева направо. Сначала вычтем два из одиннадцати:

11 − 2 = 9

Затем прибавим к результату пять и в итоге получим четырнадцать:

9 + 5 = 14

Вот запись всего решения: 11 − 2 + 5 = 9 + 5 = 14.

Ответ: 14.

Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 × 7 : 5?

Как рассуждаем:

Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Сначала выполняем деление десяти на два:

10 : 2 = 5

Теперь результат умножаем на семь:

5 × 7 = 35

И получившееся в число делим на пять:

35 : 5 = 7

Запись всего решения выглядит так: 10 : 2 × 7 : 5 = 5 × 7 : 5 = 35 : 5 = 7.

Ответ: 7.

Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.

Например, в такой последовательности можно решить пример по действиям:

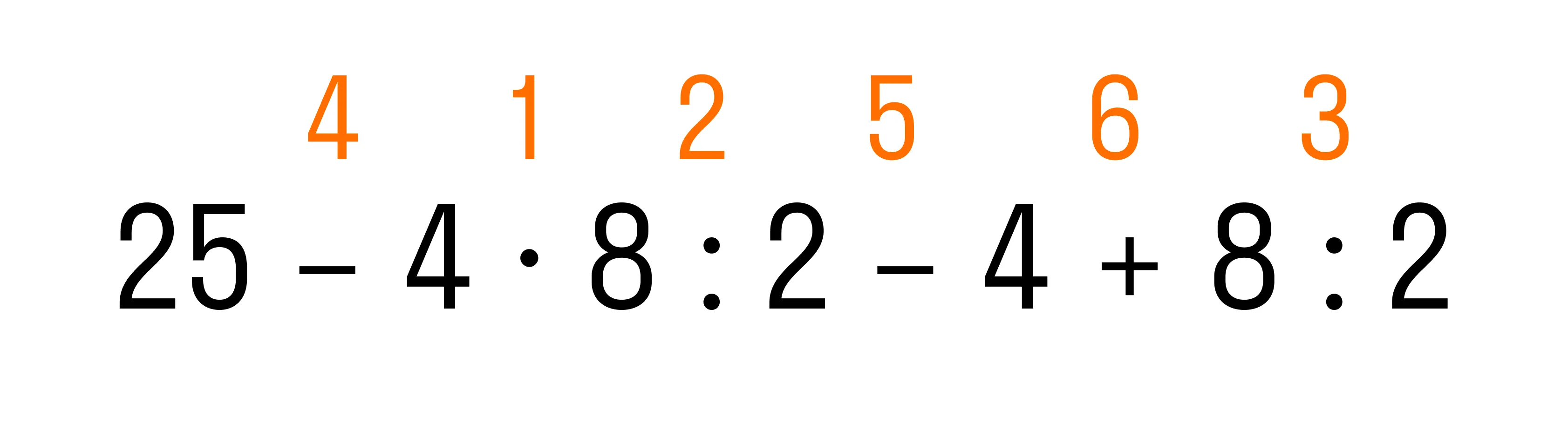
Получи больше пользы от Skysmart:

• Прокачивай знания на курсах математики.

• Выбирай из 1200+ репетиторов по математике.

• Записывайся на бесплатные курсы для детей.

Действия первой и второй ступени

В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.

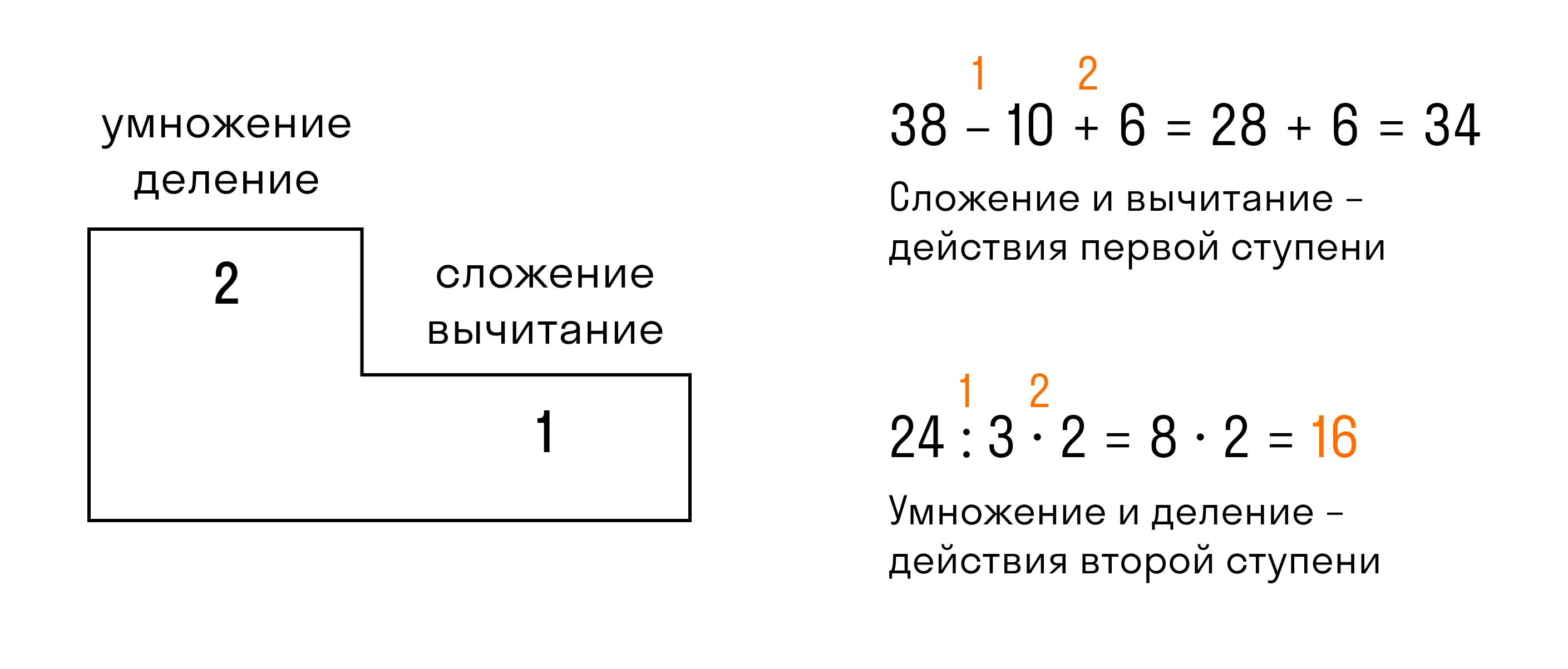
• Действиями первой ступени называют сложение и вычитание, а умножение и деление — действиями второй ступени.

С этими терминами правило определения порядка выполнения действий звучит так:

Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).

Порядок вычислений в выражениях со скобками

Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:

Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.

Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.

Рассмотрим порядок выполнения действий на примерах со скобками.

Пример 1. Вычислить: 10 + (8 − 2 × 3) × (12 − 4) : 2.

Как правильно решить пример:

Сначала определим порядок действий. Выражение содержит скобки, поэтому сначала будем выполнять действия в выражениях, которые заключены в эти скобки.

Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание.

Итак, мы определили первые три действия:

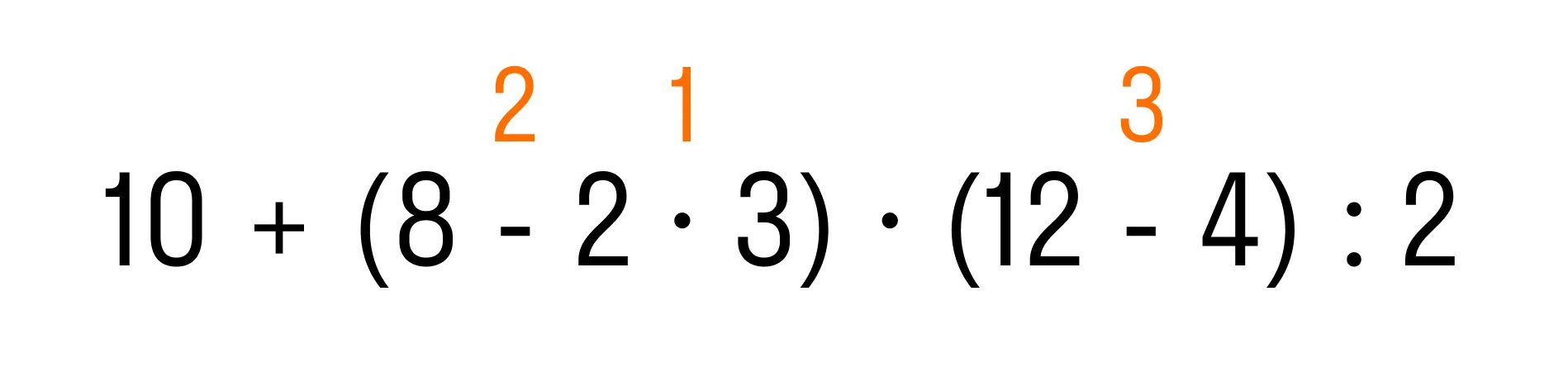
Когда выполнены все действия в скобках, по правилу дальше мы должны выполнить умножение и деление, и в последнюю очередь — сложение. Теперь мы знаем, в каком порядке решать пример:

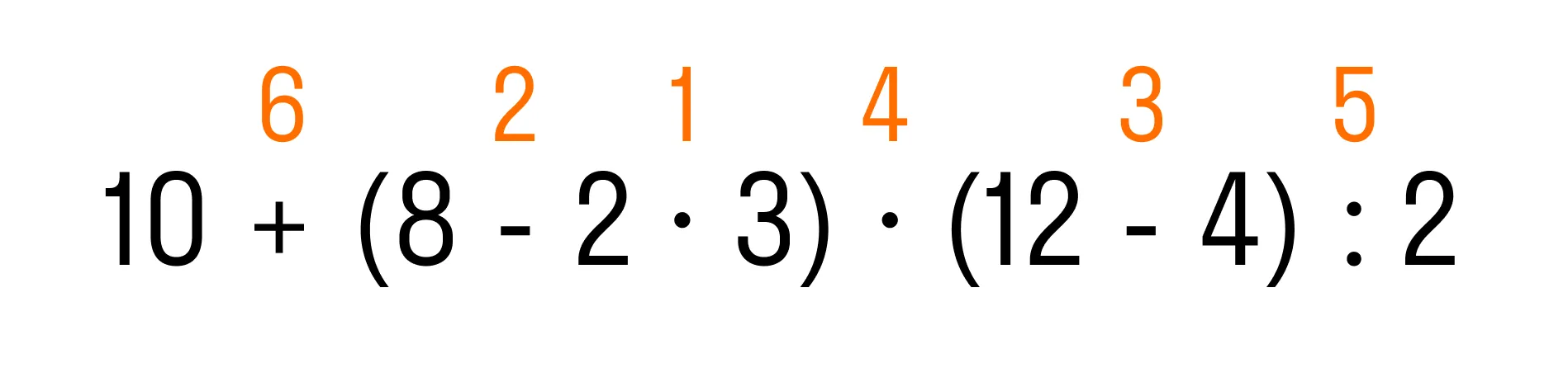
Осталось решить пример по действиям:

1. 2 × 3 = 6
2. 8 − 6 = 2
3. 12 − 4 = 8
4. 2 × 8 = 16
5. 16 : 2 = 8
6. 10 + 8 = 18

На этом все действия выполнены.

Ответ: 10 + (7 − 2 × 3) × (12 − 4) : 2 = 18.

Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.

Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 × (2 + 3)).

Как решаем:

Для начала определим порядок действий

Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 × (2 + 3). Но это выражение также содержит скобки, поэтому начнем сначала с действий в них:

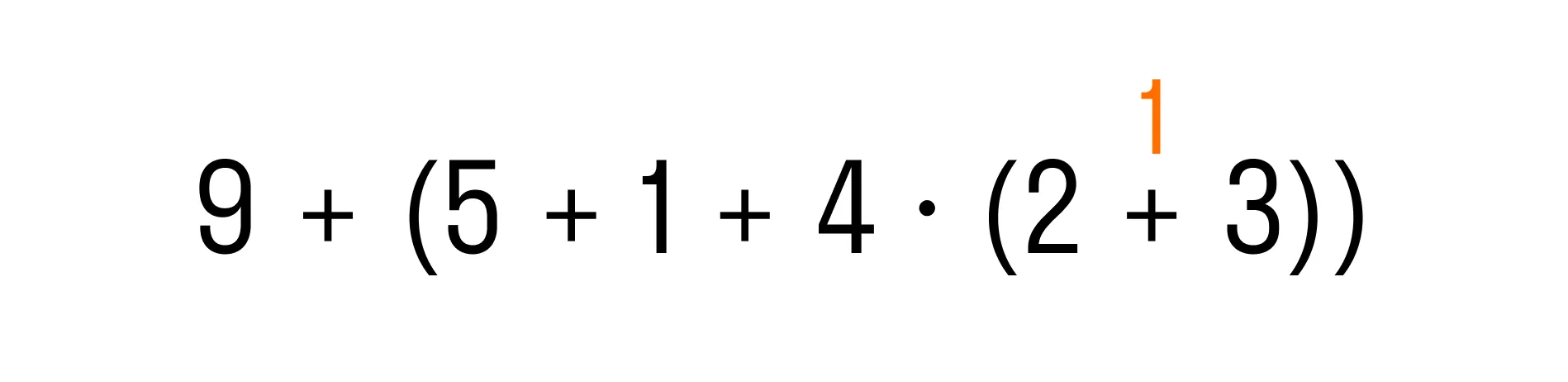
Теперь перейдем к выражению во внешних скобках. Первым действием по правилу будет умножение, а затем слева направо — две операции сложения:

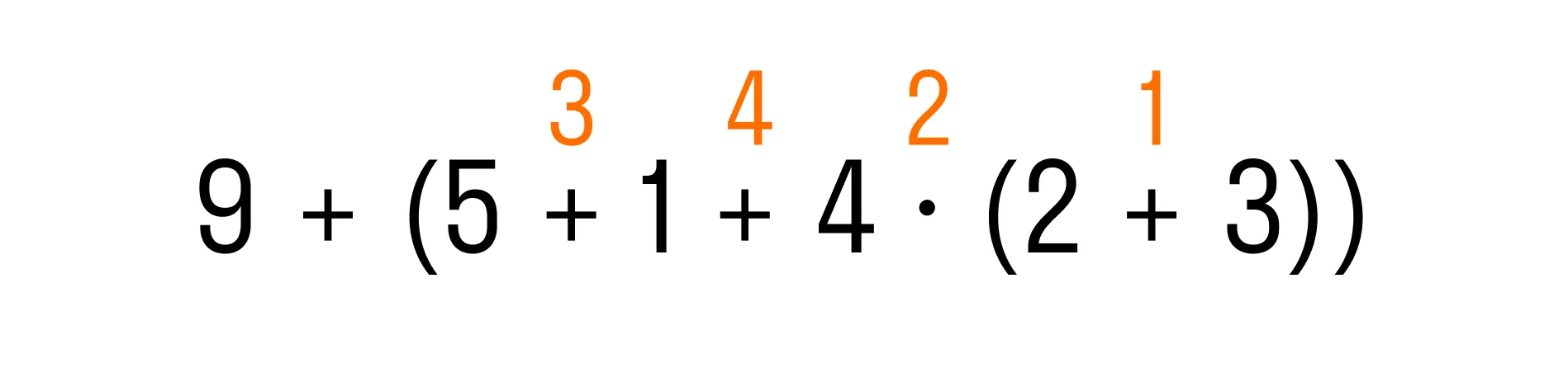
И последним действием останется выполнить сложение:

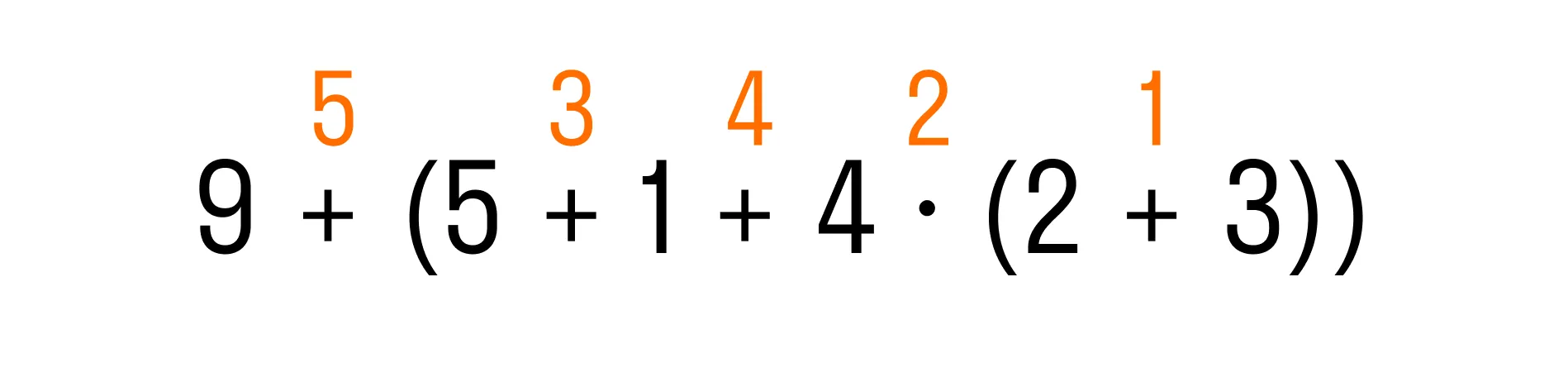
Вычисляем по действиям:

1. 2 + 3 = 5

2. 4 × 5 = 20

3. 5 + 1 = 6

4. 6 + 20 = 26

5. 9 + 26 = 35

Ответ: 4 + (3 + 1 + 4 × (2 + 3)) = 35.

Что мы узнали

1. Сначала мы вычисляем значения выражений в скобках (если они есть).

2. В выражениях без скобок мы выполняем действия слева направо.

3. Сложение и вычитание выполняем после умножения и деления.

4. Чтобы не запутаться, сначала стоит расставить порядок действий над примером, а затем решать его по действиям.

Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!