Умножение и деление степеней

Что такое степень числа

Алгебра дает нам такое определение: 

«Степенью n числа а является произведение множителей величиной а n-раз подряд»

• aⁿ — степень, где

a — основание степени

n — показатель степени

Соответственно:

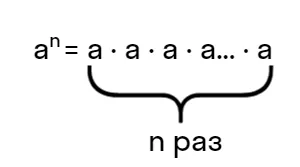
Читается такое выражение, как a в степени n

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) на само себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число — она решается довольно просто:

• 2³ = 2·2·2, где

2 — основание степени

3 — показатель степени

Соглашаюсь на обработку персональных данных в соответствии с условиями пользовательского соглашения

← Далее →

Скачать

Modal window id: popup-professionsbox

Таблица степеней

Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3). Не важно, в какой класс перешел ребенок — таблица пригодится всегда.

Число	Вторая степень	Третья степень
1	1	1
2	4	8
3	9	27
4	16	64
5	25	125
6	36	216
7	49	343
8	64	512
9	81	729
10	100	1000

178.1K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Прокачивай знания на курсах математики.

• Выбирай из 1200+ репетиторов по математике.

• Записывайся на бесплатные курсы для детей.

Свойства степеней: когда складывать, а когда вычитать

Степень в математике с натуральным показателем имеет несколько важных свойств, которые позволяют упрощать вычисления. Рассмотрим основные из них.

Свойство 1: произведение степеней

При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:

a^m · aⁿ = a^m+n

a — основание степени

m, n — показатели степени, любые натуральные числа.

Раз

3⁵ · 3³ = 3⁵⁺³ = 3⁸ = 6 561

Два

2⁸ · 2³= 2⁸⁺³ = 2¹¹ = 2048

Свойство 2: частное степеней

Когда мы делим степени с одинаковыми основаниями, основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.

, где

a — любое число, не равное нулю

m, n — любые натуральные числа такие, что m > n

Раз

Два

Свойство 3: возведение степени в степень

Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.

(aⁿ)^m = a^{n· m} 

a — основание степени (не равное нулю)

m, n — показатели степени, натуральное число

Свойство 4: возведение произведения в степень

При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.

(a · b)ⁿ = aⁿ · bⁿ

a, b — основания, не равные нулю

n — показатель степени, натуральное число

Свойство 5: возведение частного в степень

Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.

(a : b)ⁿ = aⁿ : bⁿ

a, b — основания степени, не равные нулю

n — показатель степени, натуральное число

Умножение степеней с одинаковым показателем

Для того, чтобы произвести умножение степеней с одинаковыми показателями, нужно перемножить основания, а показатель степени оставить неизменным:

aⁿ · bⁿ = (a · b)ⁿ , где

a, b — основания степени (не равные нулю)

n — показатель степени, натуральное число

• a⁵ · b⁵ = (a·a·a·a·a) ·(b·b·b·b·b) = (ab)·(ab)·(ab)·(ab)·(ab) = (ab)⁵
• 3⁵ · 4⁵ = (3·4)⁵ = 12⁵ = 248 832
• 16a² = 4²·a² = (4a)²

Деление чисел с одинаковыми степенями

При делении степеней с одинаковыми показателями результат частного этих чисел возводится в степень:

aⁿ : bⁿ = (a : b)ⁿ , где 

a, b — основания степени (не равные нулю), любые рациональные числа, b ≠ 0, 

n — показатель степени, натуральное число