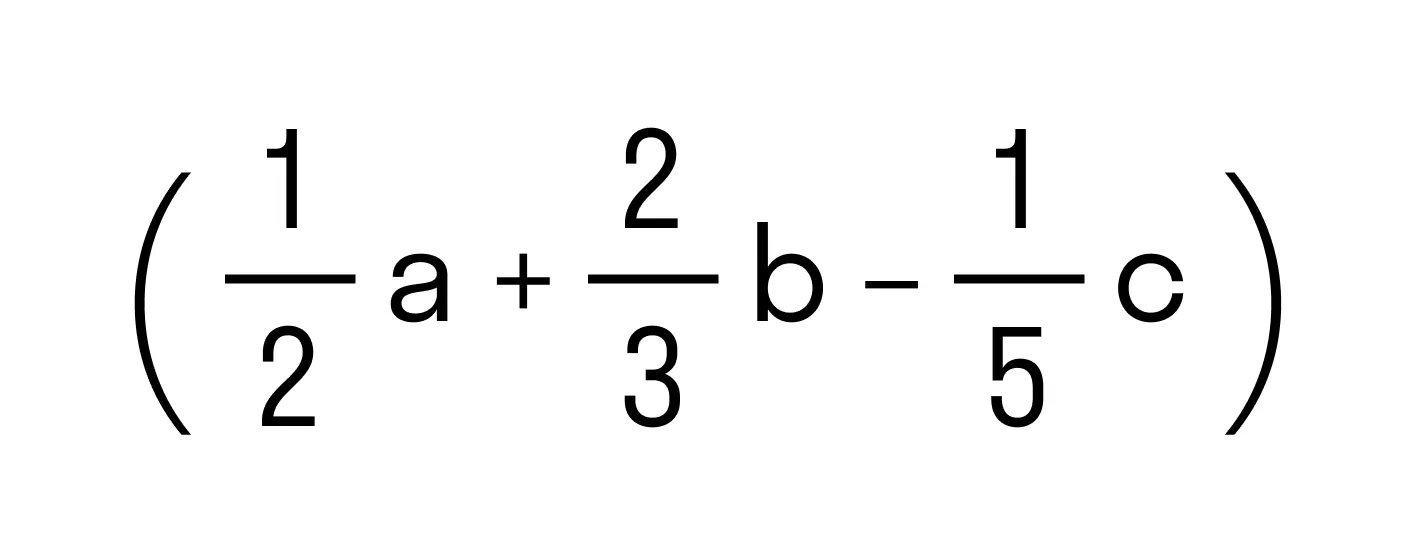Для кого эта статья:
- Ученики 6-7 классов, изучающие математику
- Учителя и репетиторы, объясняющие концепцию раскрытия скобок
- Родители, помогающие детям с домашними заданиями по математике
Понятие раскрытия скобок
В задачах по математике постоянно встречаются числовые и буквенные выражения, а также выражения с переменными, которые составлены с использованием скобок.
Основная функция скобок — менять порядок действий при вычислениях значений числовых выражений.
Часто можно перейти от одного выражения со скобками к тождественно равному выражению без скобок. Например:
- 2(3 + 4) = 2 * 3 + 2 * 4.
Такой переход от выражения со скобками к тождественно равному выражению без скобок несет в себе основную идею о раскрытии скобок.
Начальное выражение со скобками и результат, полученный после раскрытия скобок, удобно записывать в виде равенства, как мы это сделали в предыдущем примере.
В школе тему раскрытия скобок обычно подходят в 6 классе. На этом этапе раскрытие скобок воспринимают, как избавление от скобок, которые указывают порядок выполнения действий. И изучают раскрытие скобок на примерах выражений, которые содержат:
- знаки плюс или минус перед скобками, которые заключают сумму или разность, например, (a + 7) и -(-3 + 2a - 12 - b);
- произведение числа, одной или нескольких букв и суммы или разности в скобках, например, 3(2 - 7), (3 - a + 8c)(-b) или -2a(b + 2c - 3m).
Раскрытие скобок также можно рассматривать шире.
Раскрытием скобок можно назвать переход от выражения, которое содержит отрицательные числа в скобках, к выражению без скобок. Например:
- 5 + (-3) - (-7) = 5 - 3 + 7.
Или, если в описанных выше выражениях вместо чисел и переменных могут быть любые выражения. В полученных таким способом выражениях тоже можно проводить раскрытие скобок. Например:
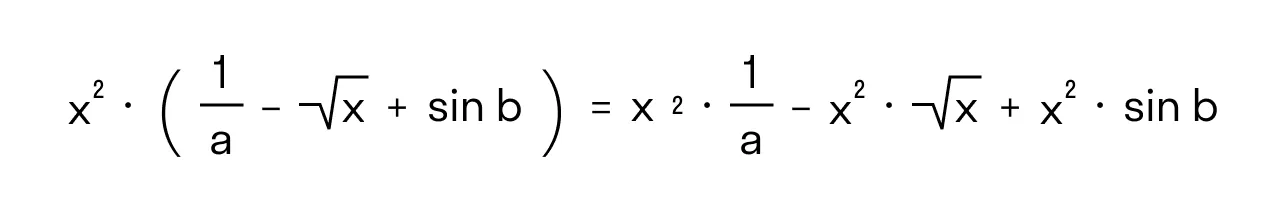
Раскрытие скобок — это избавление от скобок, которые указывают порядок выполнения действий, а также избавление от скобок, в которые заключены отдельные числа и выражения.
Важно отметить еще один момент, который касается особенностей записи решения при раскрытии скобок. При раскрытии скобок в громоздких выражениях можно прописывать промежуточные результаты в виде цепочки равенств. Например, вот так:
- 5 - (3 - (2 - 1)) = 5 - (3 - 2 + 1) = 5 - 3 + 2 - 1
Первое правило раскрытия скобок
Рассмотрим выражение:
- 8 + (−9 + 3)
Это выражение равно двум. А теперь раскроем скобки, то есть избавимся от них. Мы ожидаем, что после избавления от скобок значение выражения 8 + (−9 + 3) также должно быть равно 2.
|
Первое правило раскрытия скобок Если перед скобками стоит знак плюс — все числа, которые стоят внутри скобок, сохраняют свой знак. Формула раскрытия скобок (a − b) = a - b |
Мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Значит плюс нужно опустить вместе со скобками. То, что было в скобках — запишем без изменений, вот так:
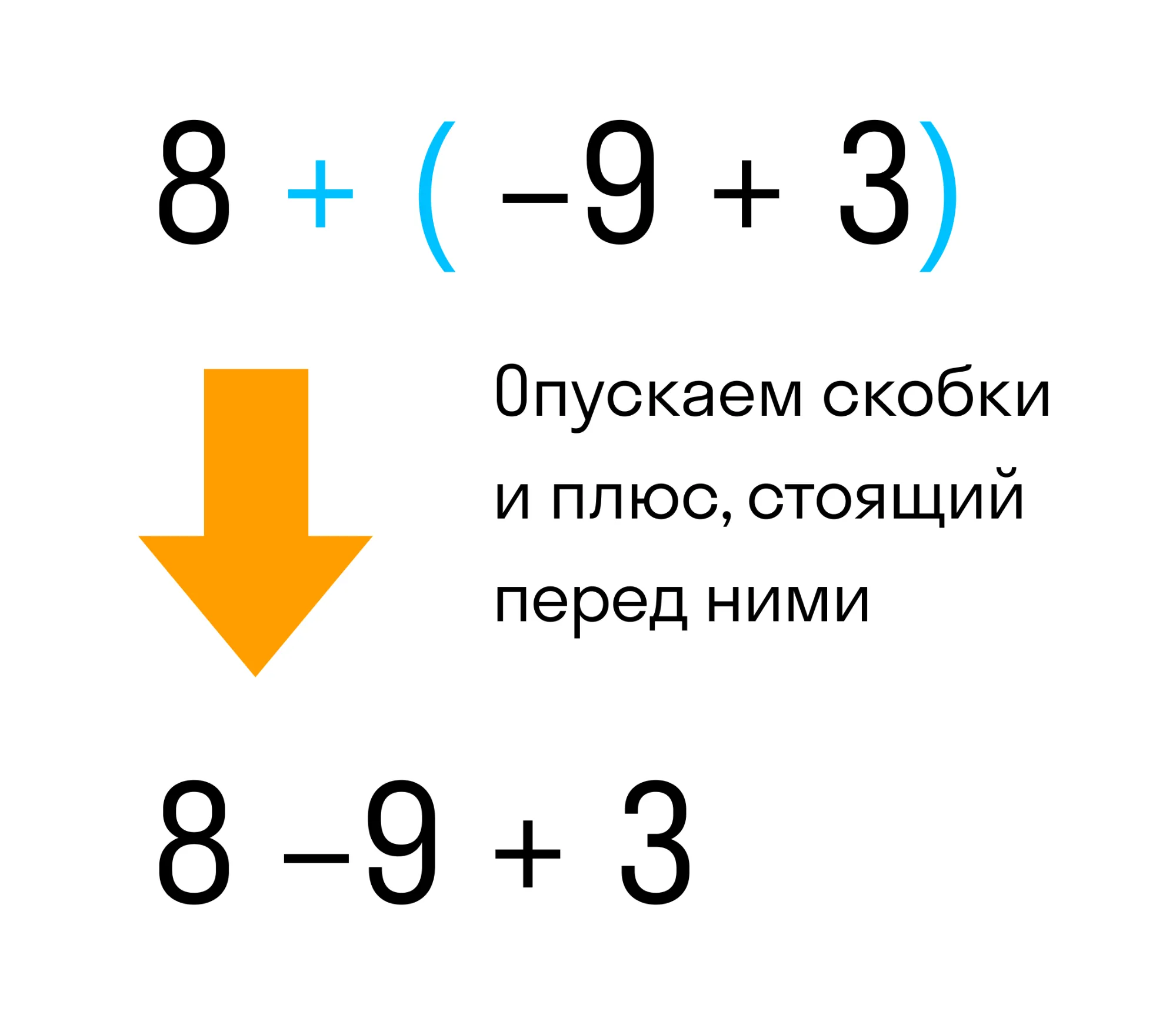
Так мы получили выражение без скобок 8 − 9 + 3. Снова получаем в результате вычисления два.
- 8 + (−9 + 3) = 2
- 8 − 9 + 3 = 2
Поэтому между выражениями 8 + (−9 + 3) и 8 − 9 + 3 можно поставить знак равенства, поскольку они равны одному и тому же значению:
- 8 + (−9 + 3) = 8 − 9 + 3
- 2 = 2
Потренируемся применять правило на примерах.
Пример 1. Раскрыть скобки в выражении 8 + (−3 − 1)
Как рассуждаем:
Перед скобками стоит плюс, значит этот плюс опустим вместе со скобками. А то, что было в скобках оставим без изменений:
- 8 + (−3 − 1) = 8 − 3 − 1
Пример 2. Раскрыть скобки в выражении 6 + (−2)
Как рассуждаем:
Перед скобками стоит плюс, значит применим то же правило:
- 6 + (−2) = 6 − 2
Раскрытие скобок в предыдущих пример выглядит, как обратная операция замены вычитания сложением.
В выражении 6 − 2 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 6 + (−2). Но если в выражении 6 + (−2) раскрыть скобки, то получится снова 6 − 2.
Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после любых других преобразований.
Идем дальше. Теперь упростим выражение 2a + a − 5b + b.
Чтобы упростить такое выражение, нужно привести подобные слагаемые. Для этого нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:
- 2a + a - 5b + b = 2a + a + (-5b) + b = (2 + 1) * a + (-5 + 1) * b = 3a + (-4b)
Получили выражение 3a + (−4b). Раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок: опустим скобки вместе с плюсом, который стоит перед этими скобками.
- 3a + (−4b) = 3a − 4b
Таким образом, выражение 2a + a − 5b + b упрощается до 3a − 4b.
После открытия одних скобок, по пути можно найти другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в таком выражении:
- 2 + (−3 + 1) + 3 + (−6)
Здесь нужно раскрыть скобки в двух местах. Снова применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед:
- 2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6
Пример 3. Раскрыть скобки 6 + (−3) + (−2)
Как рассуждаем:
В обоих местах перед скобками стоит плюс. Применяем первое правило раскрытия скобок:
- 6 + (−3) + (−2) = 6 − 3 − 2
Можно встретить такой пример, когда первое слагаемое в скобках записано без знака. Например, в выражении 1 + (2 + 3 − 4) первое слагаемое в скобках 2 записано без знака. Какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ интуитивно понятен — перед двойкой будет стоять плюс.
Дело в том, что даже в скобках перед двойкой стоит плюс, просто мы его не видим так как плюс не принято записывать. Полная запись положительных чисел выглядит так: +1, +2, +3, но плюсы по традиции не записывают, поэтому положительные числа мы всегда видим в таком виде: 1, 2, 3.
Поэтому, чтобы раскрыть скобки в выражении 1 + (2 + 3 − 4), нужно как обычно опустить скобки вместе с плюсом, который стоит перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:
- 1 + (2 + 3 − 4) = 1 + 2 + 3 − 4
Пример 4. Раскрыть скобки в выражении (−7)
Как рассуждаем:
Перед скобками стоит плюс, но мы его не видим так как до него нет других чисел или выражений. Убираем скобки, применив первое правило раскрытия скобок:
- (−7) = −7
Пример 5. Раскрыть скобки 9a + (−5b + 6c) + 2a + (−2d)
Как рассуждаем:
Видим два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишем без изменений:
- −
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Получи больше пользы от Skysmart:
-
Прокачивай знания на курсах математики
-
Выбирай из 1200+ репетиторов по математике
Записывайся на бесплатные курсы для детей
Второе правило раскрытия скобок
Здесь рассмотрим второе правило раскрытия скобок. Звучит так:
|
Второе правило раскрытия скобок Если перед скобками стоит знак минус — все числа, которые стоят внутри скобок, меняют свой знак на противоположный. Формула раскрытия скобок −(a − b) = −a + b |
Например, раскроем скобки в выражении 5 − (−2 − 3)
Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:
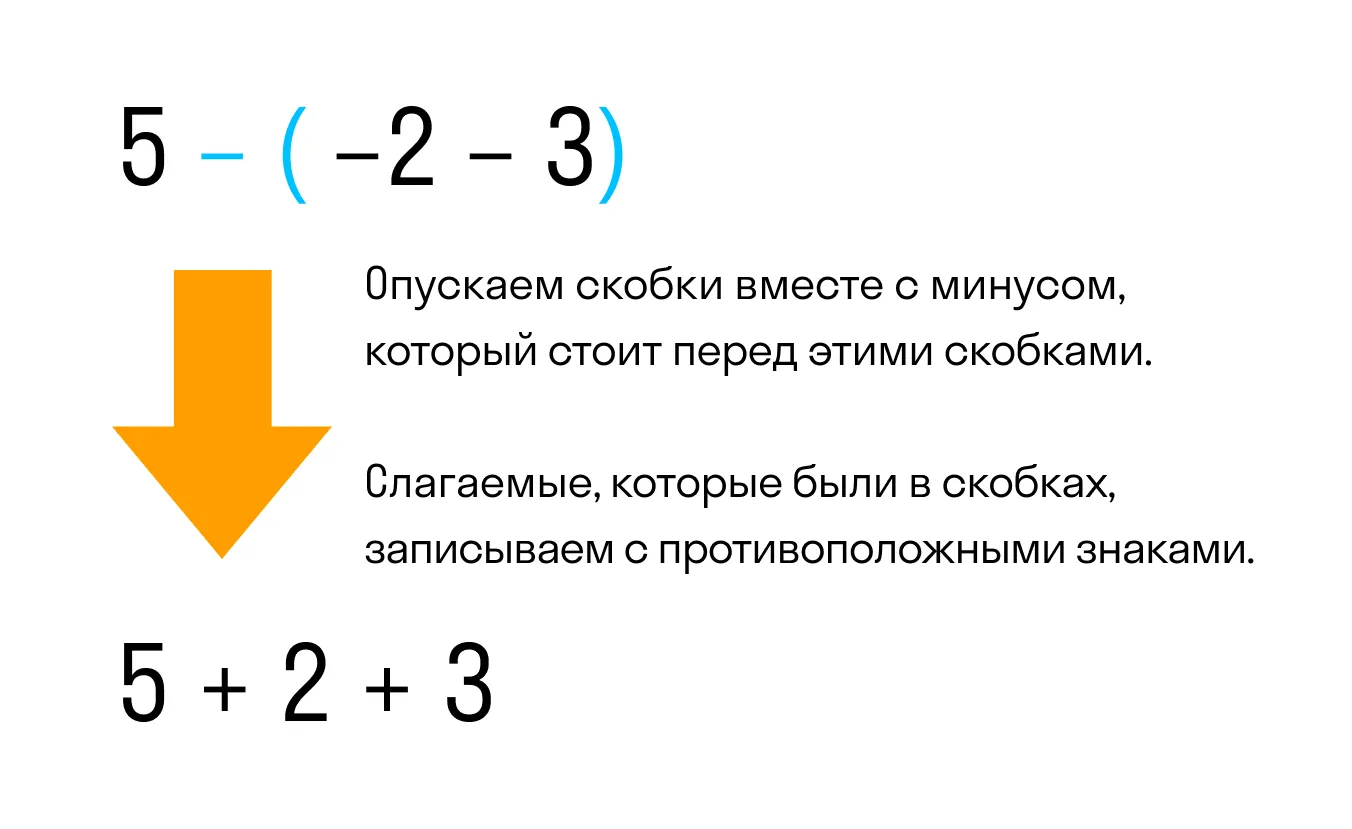
Так мы получили выражение без скобок 5 + 2 + 3. Это выражение равно десяти, как и предыдущее выражение со скобками было равно 10.
- 5 − (−2 − 3) = 10
- 5 + 2 + 3 = 10
Поэтому между выражениями 5 − (−2 − 3) и 5 + 2 + 3 можно поставить знак равенства так как они равны одному и тому же значению:
- 5 − (−2 − 3) = 5 + 2 + 3
- 10 = 10
Пример 1. Раскрыть скобки в выражении 18 − (−1 − 5)
Как рассуждаем:
Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:
18 − (−1 − 5) = 18 + 1 + 5
Пример 2. Раскрыть скобки −(−6 + 7)
Как рассуждаем:
Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:
−(−6 + 7) = 6 − 7
Пример 3. Раскрыть скобки −(−7 − 4) + 15 + (−6 − 2)
Как рассуждаем:
Здесь мы видим два места, где нужно раскрыть скобки. В первом случае применим второе правило раскрытия скобок, а во втором — первое правило:
−(−7 − 4) + 15 + (−6 − 2) = 7 + 4 + 15 − 6 − 2
Пример 4. Раскрыть скобки в выражении a − (3b + 3) + 10
Как рассуждаем:
Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:
a − (3b + 3) + 10 = a − 3b − 3 + 10
Другие правила раскрытия скобок
|
Правило раскрытия скобок при делении Если после скобок стоит знак деления — каждое число внутри скобок делится на делитель, который стоит после скобок. Формула раскрытия скобок (a + b) : c = a/c + b/c. |
Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые.
Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.
Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2/3. Для этого сначала заменим деление умножением на обратное число:
- (x + 2) : 2/3 = (x + 2) * 3/2.
Далее умножим скобку на число:
- (x + 2) * 3/2 = x * 3/2 + 2 * 3/2.
|
Правило раскрытия скобок при умножении: Если перед скобками стоит знак умножения — каждое число, которое стоит внутри скобок, нужно умножить на множитель перед скобками. Формула раскрытия скобок a(b + c) = ab + ac |
Пример 1. Раскрыть скобки 5(3 − x)
Как решаем:
В скобке у нас стоят 3 и −x, а перед скобкой — пятерка. Значит, каждый член скобки нужно умножить на 5:
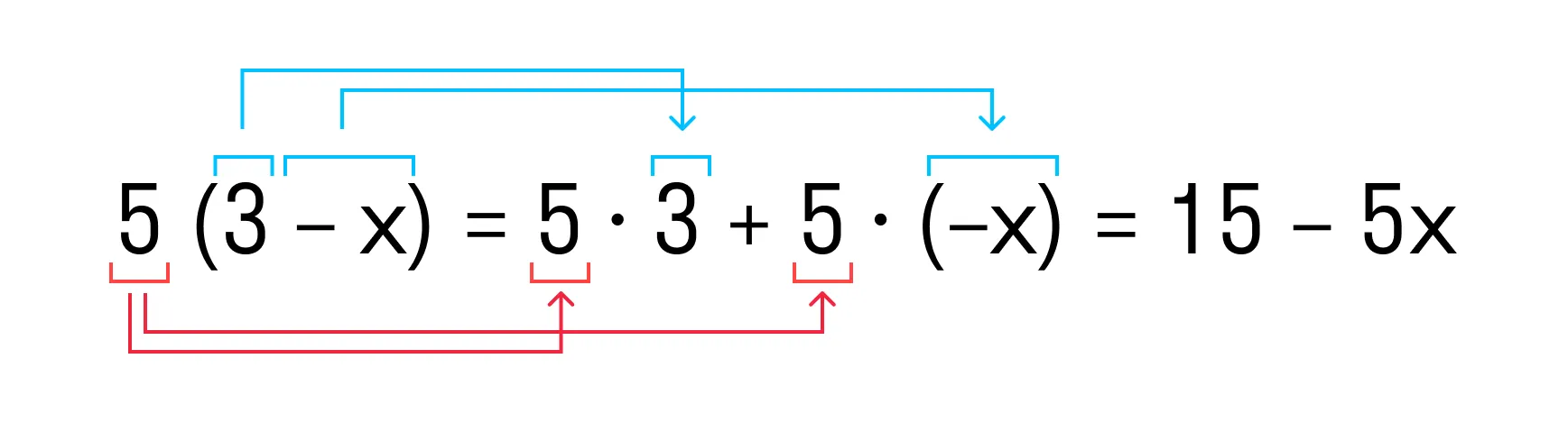
Знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.
Пример 2. Упростить выражение: 5(x + y) − 2(x − y)
Как решаем: 5(x + y) − 2(x − y) = 5x + 5y − 2x + 2y = 3x + 7y.
Таблица с формулами раскрытия скобок
Эти таблицы с правилами раскрытия скобок можно распечатать и обращаться к ним, когда возникнут сомнения в ходе решения задачки.
|
Правила раскрытия круглых скобок вида (-a), в которых находится одночлен |
|
|
При сложении: b + (-a) = b - a b - (-a) = b + a (-a) + b = -a + b |
При умножении: (-a)b = -ab a(-b) = -ab (-a)(-b) = ab |
|
Правила раскрытия круглых скобок, в которых находится многочлен |
|
Скобки убирают, знаки всех слагаемых в скобках не меняют, если:
a + (b - c + d) = a + b - c + d
(a+b-c)+d=a+b-c+d |
|
Скобки убирают, знаки всех слагаемых в скобках меняются на противоположные, если:
a - (b - c + d) = a - b + c - d
-(a + b - c) + d = -a - b + c + d |
|
Раскрытие круглых скобок при умножении одночлена на многочлен |
|
a + b(c + d - f + e) = a + bc + bd - bf + be a + b(c + d - f + e) = a + bc + bd - bf + be -a(b + c - d) + f = -ab - ac + ad + f |
|
Раскрытие круглых скобок при умножении многочлена на многочлен |
|
(a + b)(c - d) = a(c - d) + b(c - d) = ac - ad + bc - bd (-a + b)(c + d) = -a(c + d) + b(c + d)= -ac - ad + bc + bd |
|
Раскрытие круглых скобок при возведении многочлена в степень |
|
(a + b)2 = (a + b)(a + b) = a(a + b) + b(a + b)= a2 + ab + ab + b2 = a2 + 2ab + b2 |
Скобка в скобке
В 7 классе на алгебре можно встретить задачи со скобками, которые вложены внутрь других скобок. Вот пример такого задания:
- упростить выражение 7x + 2(5 − (3 x + y)).
Чтобы успешно решать подобные задания, нужно:
- внимательно разобраться со скобками — какая в какой находится.
- раскрывать скобки последовательно, начиная с самой внутренней.
При этом важно при раскрытии одной из скобок не трогать все остальное выражение и просто переписывать его, как есть. Разберем подробнее тот же самый пример.
Пример 1. Раскрыть скобки и привести подобные слагаемые 7x + 2(5 − (3x + y))
Как решаем:
Начнем с раскрытия внутренней скобки (той, что внутри). Раскрывая ее, имеем дело только с тем, что к ней непосредственно относится – это сама скобка и минус перед ней. Всё остальное переписываем также как было.
- 7x + 2(5 − (3x + y)) = 7x + 2(5 − 3 x − y).
Теперь раскроем вторую скобку, внешнюю:
- 7x + 2(5 − (3x + y)) = 7x + 2(5 − 3 x − y) = 7 x + 2 * 5 − 2 * 3 x − 2 * y.
Упростим получившееся выражение:
- 7x + 2(5 − (3x + y)) = 7x + 2(5 − 3 x − y) = 7 x + 2 * 5 − 2 * 3 x − 2 * y = 7x + 10 − 6x − 2y.
Приведем подобные:
- 7x + 10 − 6x − 2y = x + 10 − 2y
Готово!
Порядок раскрытия скобок
Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида. То есть в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.
Порядок раскрытия скобок согласован с порядком выполнения действий:
- возвести многочлены в скобках в натуральную степень;
- слева направо провести умножение и деление;
- когда в скобках останутся только слагаемые, раскрыть скобки и привести подобные.
Пример 1. Раскрыть скобки и упростить выражение:
-(2a + 5b) + (3a - 2b + 1) - (2a + 4) = -2a - 5b + 3a - 2b + 1 - 2a - 4 = (-2a + 3a - 2a) + (-5b - 2b) + (1 - 4) = -a - 7b - 3
Пример 2. Доказать, что при любых значениях переменной a значение выражения 3(2a - 7) - (a + (5a - 4)) — отрицательно.
Доказательство:
33(2a - 7) - (a + (5a - 4)) = 3(2a - 7 ) - (a + 5a - 4)= 6a - 21 - a - 5a + 4 = (6a - a - 5a) + (-21 + 4) = -16/p>
Значение выражения не зависит от переменной и всегда отрицательно. Что и требовалось доказать.
Задачи для самостоятельного решения
На алгебре в 6 и 7 классе придется решать задачки с раскрытием скобок много и часто. Поэтому лучше запомнить правила и практиковаться уже сейчас.
Задание 1. Раскройте скобки в выражении: 2 + (6 + 3) + 2 - (1 + 1)
Задание 2. Раскройте скобки в выражении: - 21 + 14 + (-1 + 5) - 11 + ( 3 + 2)
Задание 3. Раскройте скобки в выражении: 3 * (-4m + 3n - 5)
Задание 4. Раскройте скобки в выражении: -(12a - 5b - 2)
Задание 5. Раскройте скобки в выражении: 3(x - 9)
Задание 6. Раскройте скобки:
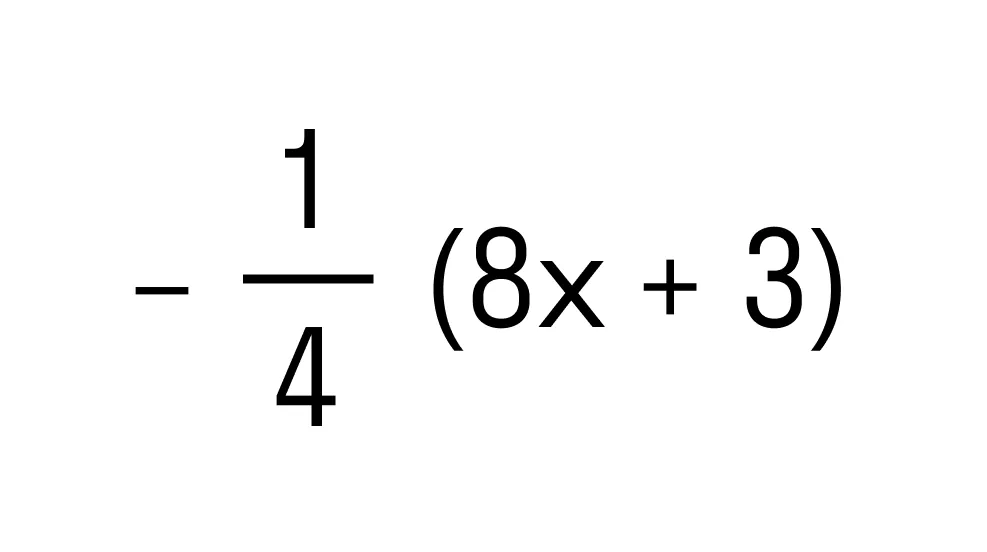
Задание 7. Раскройте скобки: