Умножение десятичных дробей

Понятие десятичной дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

• обыкновенный вид — ½ или a/b,

• десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

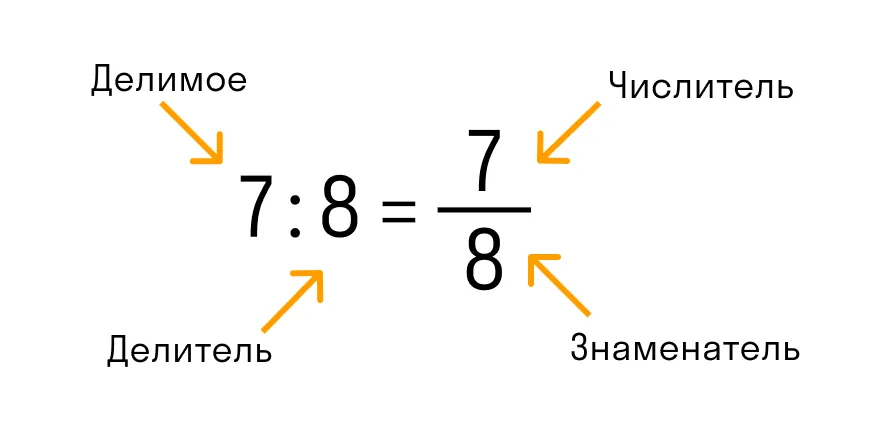
Вернемся к обыкновенным дробям позже, а сейчас обсудим десятичные дроби. Их знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

• 0,8

• 7,42

• 9,932

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Регистрируясь, вы принимаете пользовательское соглашение и политику конфиденциальности

← Далее →

Получить

Modal window id: popup-mathcomix

Свойства десятичных дробей

Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:

• 0,600 = 0,6;

• 21,10200000 = 21,102.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

• Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то она равна нулю.

• Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т. д.

• Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

106.2K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Прокачивай знания на курсах математики.

• Выбирай из 1200+ репетиторов по математике.

• Записывайся на бесплатные курсы для детей.

Как записать десятичную дробь

Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.

Пример 1. Перевести обыкновенную дробь в десятичную.

Как решаем:

1. Знаменатель равен 10 — это один ноль.

2. Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.

3. В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.

Ответ:

Пример 2. Перевести в десятичную дробь.

Как решаем:

1. Знаменатель равен 1000 — это три нуля.

2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.

3. Так как в числителе только две цифры, то на пустующие места пишем нули.

4. В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.

Ответ:

Как читать десятичную дробь

Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:

Сколько цифр после запятой?	Читается, как
одна цифра — десятых;	1,3 — одна целая, три десятых;
две цифры — сотых	2,22 — две целых, двадцать две сотых;
три цифры — тысячных;	23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных;
четыре цифры — десятитысячных;	0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных;
и т.д.

Сохраняй наглядную картинку, чтобы быстрее запомнить.

Свойства умножения

С десятичными дробями можно производить те же действия, что и с любыми другими числами: складывать и вычитать, делить и умножать. В этом блоке узнаем, как умножать дроби.

Свойства умножения десятичных дробей

Переместительное свойство умножения — от перестановки мест множителей произведение не изменяется. ab = ba Сочетательное свойство умножения — чтобы умножить число на произведение двух чисел, нужно сначала умножить его на первый множитель, затем полученное произведение умножить на второй множитель. (ab)c = a(bc) Распределительное свойство умножения относительно сложения — чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить. a(b + c) = ab + ac Распределительное свойство умножения относительно вычитания — чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе. a(b — c) = ab — ac

Умножение десятичных дробей друг на друга можно упростить и просто умножить натуральные числа. Главное — правильно поставить запятую в ответе.

Если в задаче даны десятичные дроби с разными знаками — используем правило умножения отрицательных чисел. Как быстро запомнить:

«−−»	минус на минус дает плюс
«−+»	минус на плюс дает минус
«+−»	плюс на минус дает минус
«++»	плюс на плюс дает плюс

Числа с единицей и нулями (10, 100, 1000 и т. д.) называются разрядными единицами, так как цифра 1 — единственная значимая цифра в числе и от ее местоположения зависит количественное значение числа. Важно запомнить правила для умножения и деления на разрядную единицу:

• Чтобы умножить число на разрядную единицу, достаточно к числу справа дописать столько нулей, сколько их содержит разрядная единица.

• Чтобы разделить число на разрядную единицу, достаточно от числа справа отбросить столько нулей, сколько их содержит разрядная единица.

Как умножать десятичные дроби в столбик

Чтобы перемножить десятичные дроби нужно сделать три шага:

1. Записать десятичные дроби в столбик и умножить друг на друга, как обыкновенные числа.

2. Посчитать количество знаков после запятой у каждой дроби. Сложить их количество.

3. Полученное количество знаков отсчитать справа налево и поставить запятую.

Пример: умножить 3, 11 на 0,01.

Как решаем:

1. Запишем дроби в столбик и умножим их, как будто у нас нет никаких запятых:

   

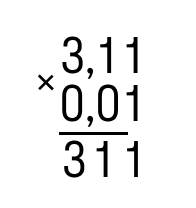
   Получаем: 311 ∗ 001 = 311.

2. Считаем общее количество цифр после запятой у обеих дробей — в нашем примере их четыре (по две на каждую).

3. Берем число, которое получилось после умножения и отсчитываем справа налево 4 знака. Но у нас получилось всего три цифры, а не четыре. Значит добавляем перед ними один ноль и вуаля — четыре цифры после запятой готовы

   

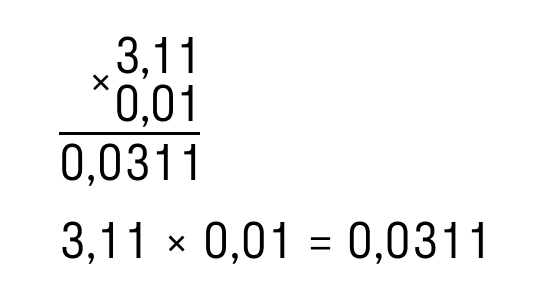
Ответ: 3,11 ∗ 0,01 = 0,0311.

Примеры умножения десятичных дробей столбиком:

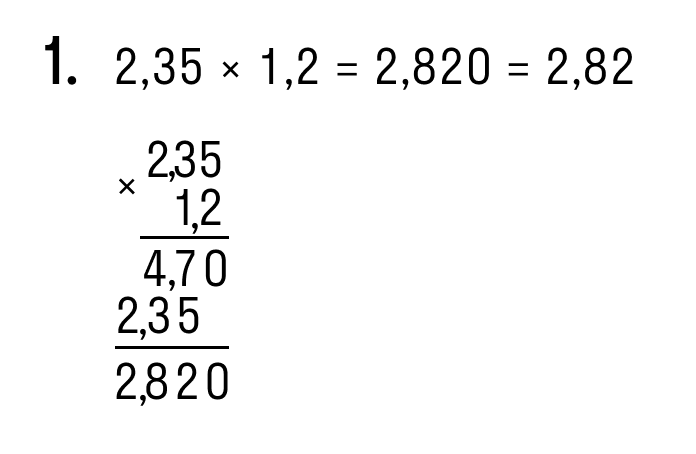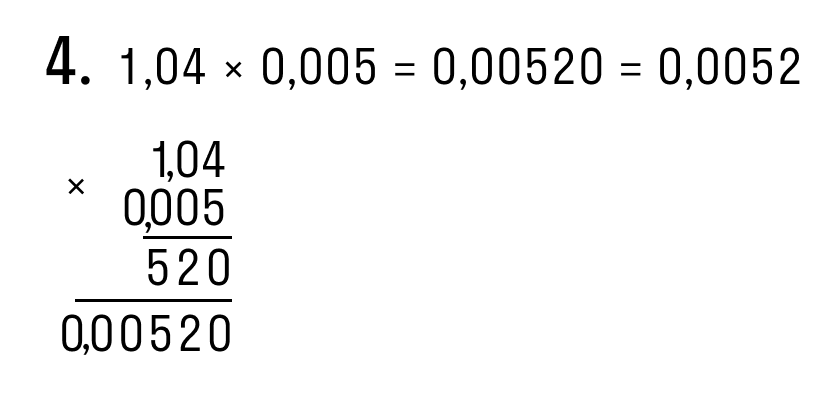Как умножать десятичные дроби на натуральные числа

Умножение десятичных дробей на обычные числа происходит так же, как и умножение между десятичными дробями. Чтобы считать быстрее, умножайте их в столбик по правилам выше. А вот и примерчики!

Пример 1. Умножить десятичную дробь 2,27 на целое число 15.

Как решаем:

умножить столбиком данные числа и отделить два знака запятой.

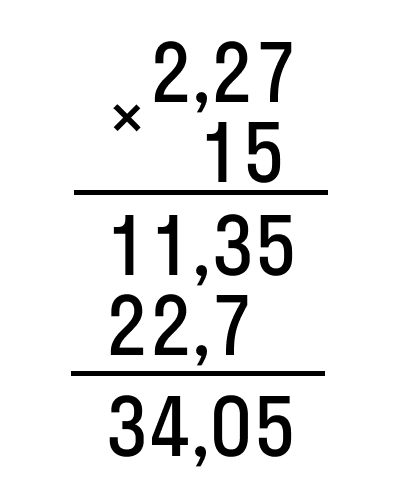
Ответ: 15 ∗ 2,27 = 34,05.

Пример 2. Умножить 11 на 0,005.

Как решаем:

умножить столбиком данные числа и отделить три знака запятой.

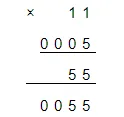
Ответ: 11 ∗ 0,005 = 0,055.

Пример 3. Умножить 0,1557.. на 3.

Как решаем:

1. Округлить бесконечную дробь:

   0,1557..≈ 0,156

2. 0,156 * 3 ≈ 0,468.

Ответ: 0,1557.. ∗ 3 ≈ 0,468.

Как умножать десятичные дроби на 10, 100, 1000

Чтобы умножить десятичную дробь на 10, 100, 1000, нужно просто перенести запятую в дроби вправо на столько знаков, сколько нулей стоит во втором множителе. Лишние нули слева можно отбросить. А если цифр не хватает — дописываем нули.

Примеры:

• 1,15 ∗ 10 = 11,5;

• 22,345 ∗ 100 = 2 234,5;

• 8,99 ∗ 1 000 = 8 990;

• 0,54678 ∗ 10 000 = 5467,8;

• 0,07 ∗ 1 000 = 70;

• 0,00033 ∗ 100 = 0,033.

Как умножать десятичные дроби на 0,1, 0,01, 0,001

Чтобы умножить десятичную дробь на 0,1, 0,01, 0,001, нужно перенести запятую в дроби влево на столько знаков, сколько нулей стоит перед единицей. Ноль целых — тоже считаем. Если цифр не хватает — просто дописываем дополнительный ноль — один или несколько — после запятой.

Примеры:

• 34,9 ∗ 0,1 = 3,49;

• 1,8 ∗ 0,1 = 0,18;

• 145,7 ∗ 0,01 = 1,457;

• 9655,1 ∗ 0,001 = 9,6551;

• 11,9 ∗ 0,0001 = 0,00119.

Как умножить десятичную дробь на обыкновенную

Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.

Пример 1. Умножить  на 0,9.

Как решаем:

1. Записать 0,9 в виде обыкновенной дроби:

2. Умножить числа по правилам

Ответ:

Пример 2. Умножить 0,18 на .

Как решаем:

1. Записать в виде десятичной дроби:

2. Произвести умножение в столбик или при помощи калькулятора:

Ответ: