Площадь прямоугольного треугольника - это половина произведения его катетов. Она вычисляется, исходя из длины двух его катетов. Формула для нахождения площади прямоугольного треугольника:
Пример: для катетов длиной 3 и 4,
Для кого эта статья:
- Студенты и школьники, изучающие геометрию и математику
- Учителя математики, ищущие ресурсы для своих уроков
- Все, кто хочет быстро вычислить площадь прямоугольного треугольника с помощью калькулятора
Онлайн-калькулятор площади прямоугольного треугольника
Формула: S = 1/2 (a × b), где a и b — катеты.
Катет a:
Катет b:
Площадь треугольника: -
Основные определения
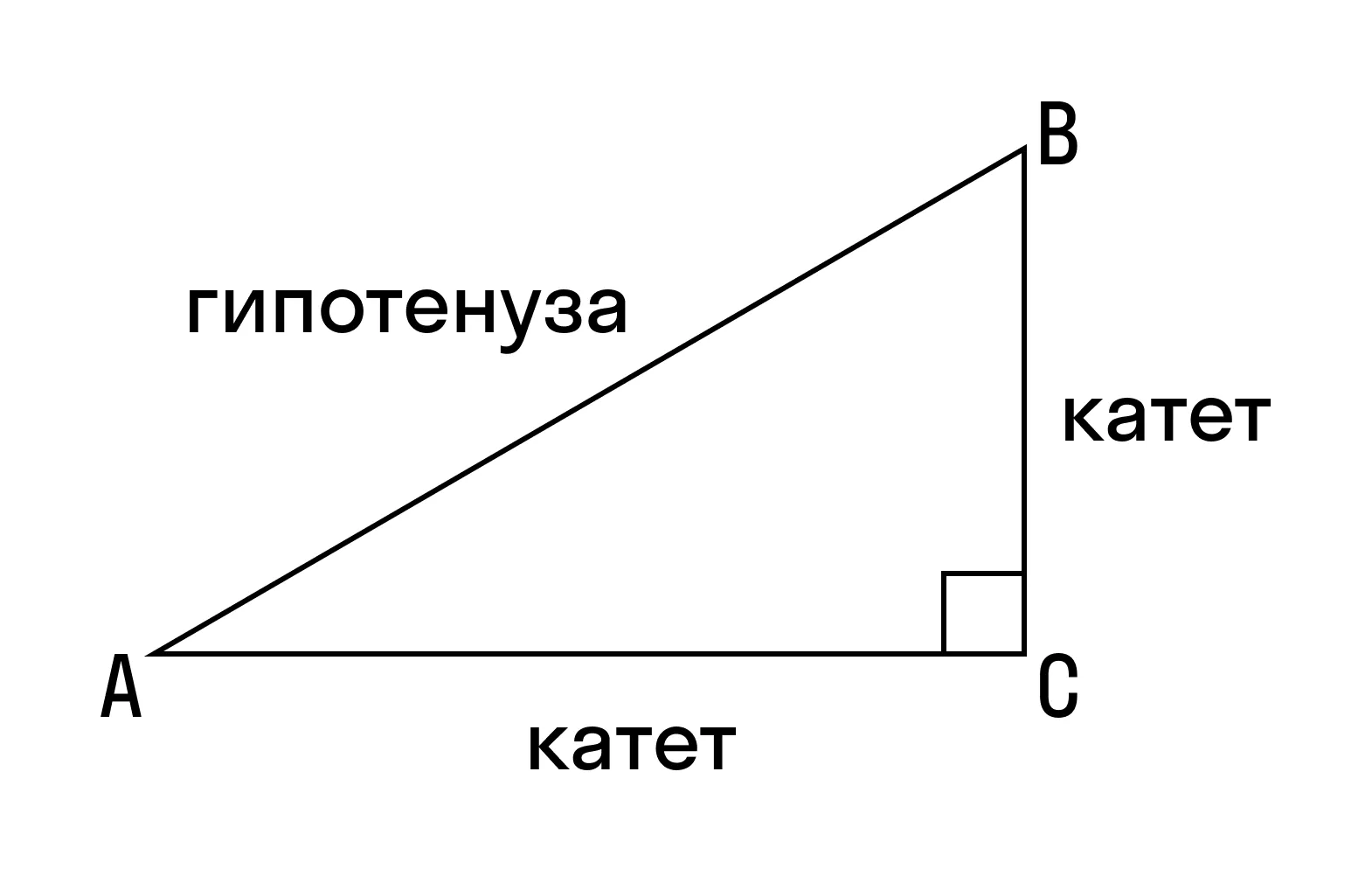
Прямоугольный треугольник — это треугольник, в котором один угол прямой, то есть равен 90˚.
Гипотенуза — это сторона, противолежащая прямому углу.
Катеты — это стороны, прилежащие к прямому углу.
Чтобы найти площадь прямоугольного треугольника, можно применить любую формулу нахождения площади треугольника — их несколько.
Получи больше пользы от Skysmart:
-
Прокачивай знания на курсах математики
-
Выбирай из 1200+ репетиторов по математике
Записывайся на бесплатные курсы для детей
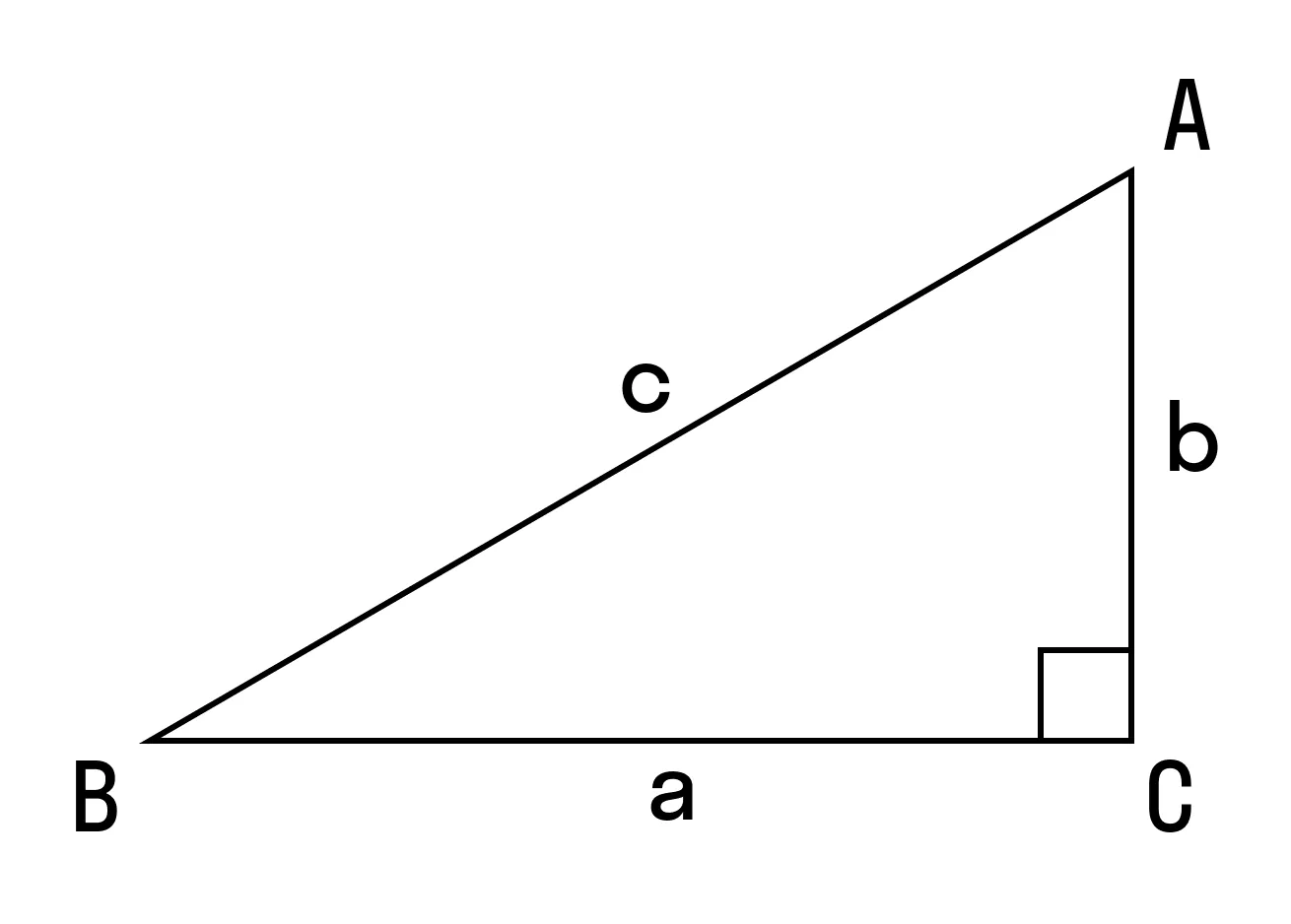
Формула для нахождения площади прямоугольного треугольника через катеты
Чтобы найти площадь, нужно вывести формулу:
|
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию. S = 1/2 (a × h) |
Так как в прямоугольном треугольнике катеты перпендикулярны, то один катет — это высота, проведенная ко второму катету.
Отсюда следует, что площадь прямоугольного треугольника равна половине произведения его катетов.
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через катеты.
S = 1/2 (a × b), где a и b — катеты
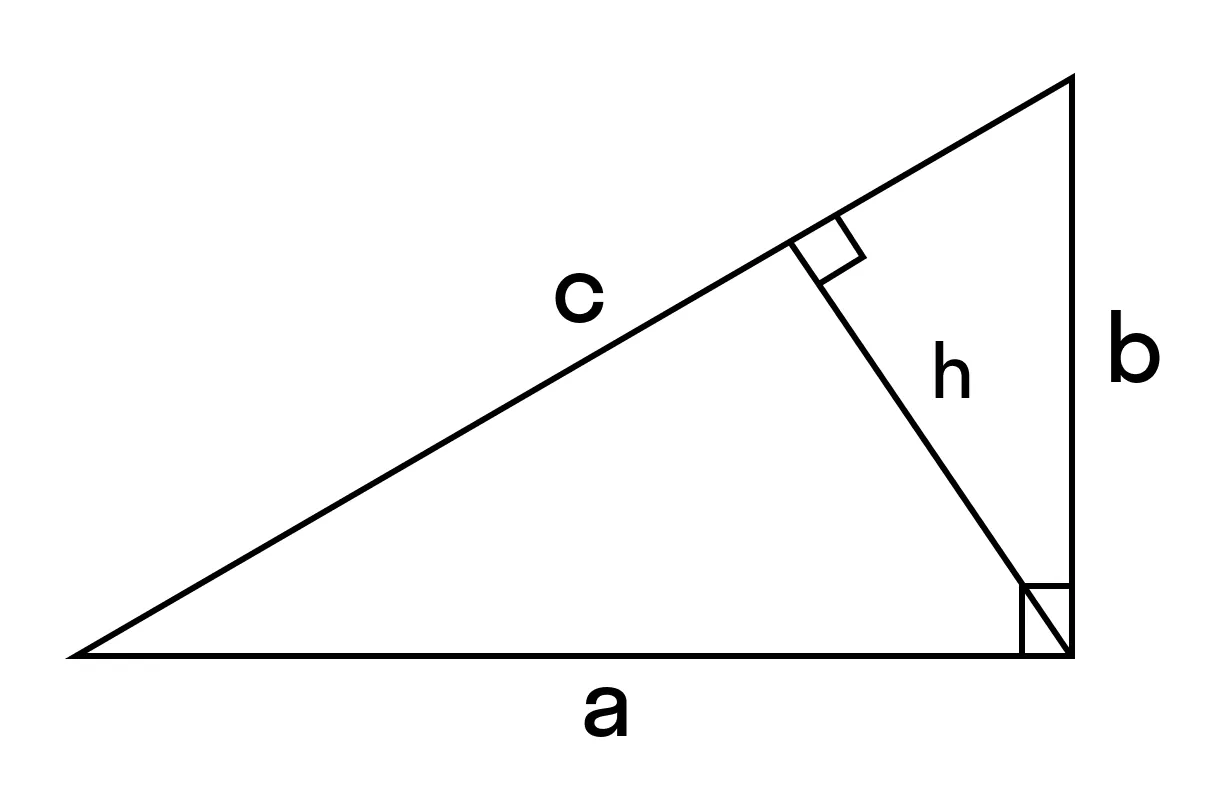
Формула для нахождения площади прямоугольного треугольника через гипотенузу
|
Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе. S = 1/2 (c × h) где с — гипотенуза, h — высота. |
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через гипотенузу.
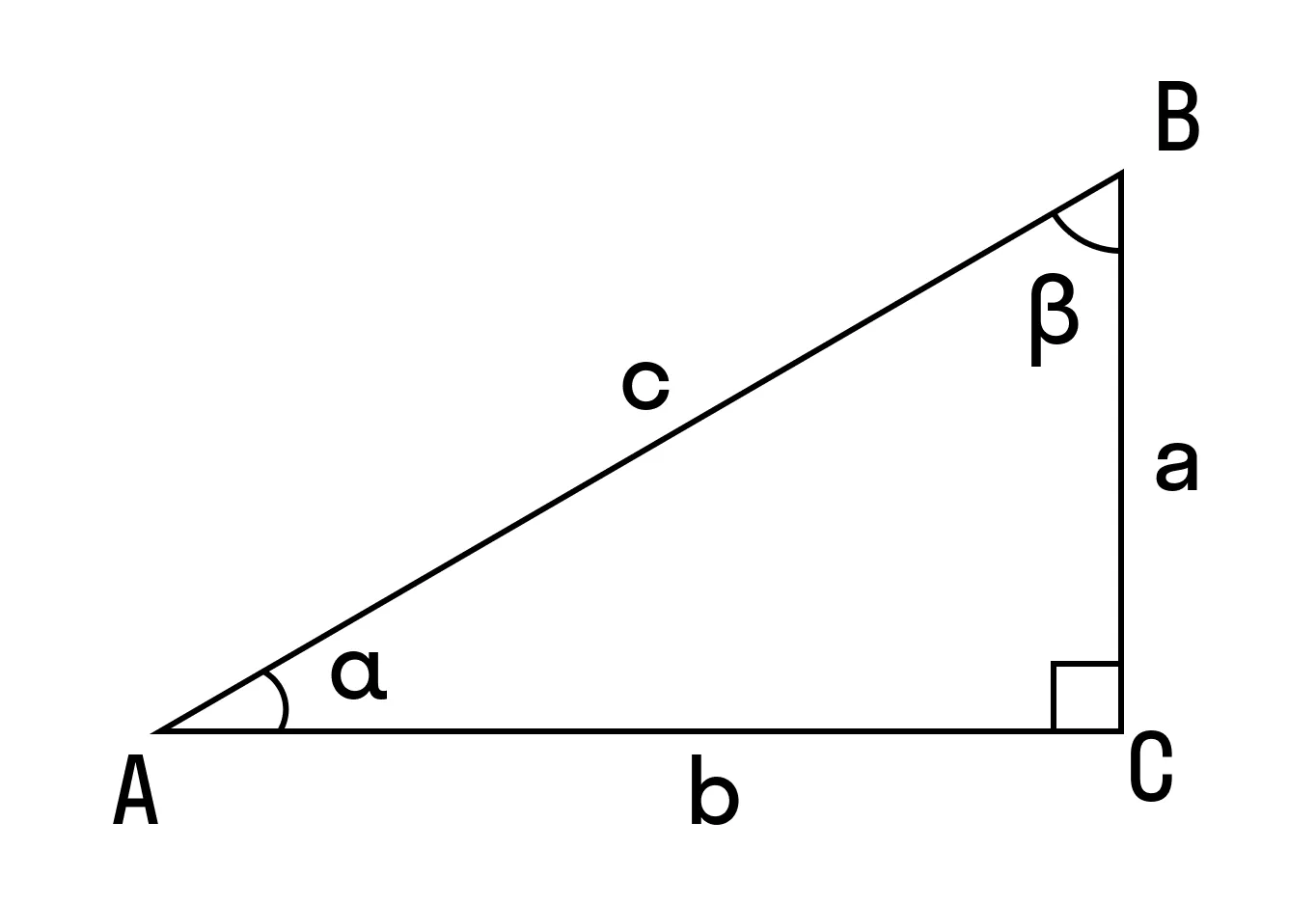
Формула для нахождения площади прямоугольного треугольника через гипотенузу и острый угол
с — гипотенуза
a, b — катеты
α, β — острые углы
Формулы нахождения площади прямоугольного треугольника через катет и угол
a и b — катеты
α, β — острые углы
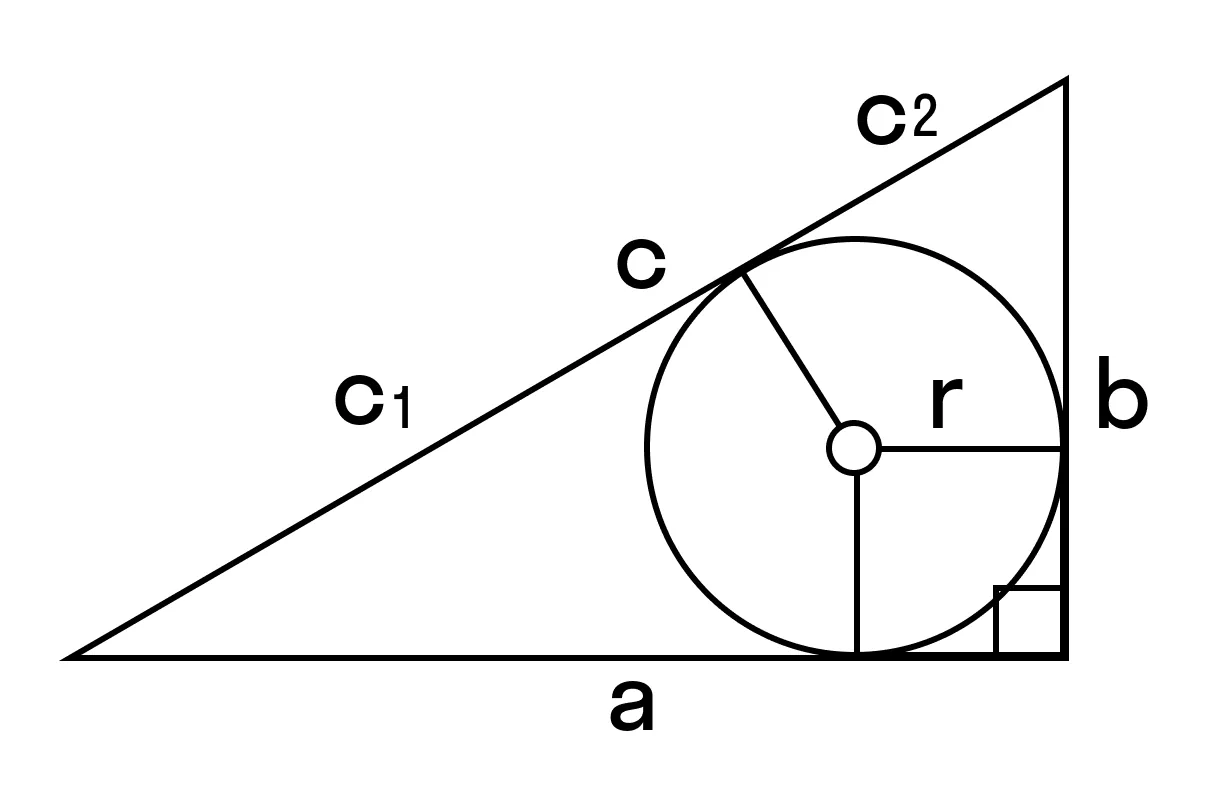
Формулы нахождения площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу
Радиус вписанной окружности выражается через катеты и гипотенузу по формуле:
r = (a + b − c) / 2
a и b — катеты
с — гипотенуза
S прямоугольного треугольника = r (r + c) = c1 × c2
r — радиус вписанной окружности
с — гипотенуза
C1 и С2 — отрезки, полученные делением гипотенузы на две части точкой касания с окружностью
Уверены, что во всем разобрались? Закрепите знания на курсах обучения математике в онлайн-школе Skysmart!




















