Сложение чисел с разными знаками - это процесс, при котором из большего модуля одного числа вычитается меньший модуль другого числа. Затем к результату добавляется знак числа с большим модулем. Например, для чисел -7 и 3 вычисление будет следующим:
- |7| - |3| = 4
- знак - (потому что у -7 больший модуль)
- итого: -4
Основные определения
Целые числа — это множество чисел, которые состоят из натуральных чисел, целых отрицательных чисел и нуля.
Отрицательные целые числа — это целые числа со знаком «минус». Они всегда меньше нуля. Примеры целых отрицательных чисел: -1, -945, -20.
Положительные целые числа — это целые числа со знаком «плюс». Они всегда больше нуля. Примеры положительных целых чисел: 11, 500, 1387.
У каждого положительного числа есть число-близнец, которое отличается только тем, что перед ним стоит знак минус. Такие числа называются противоположными.
Противоположные числа не равны друг другу, но у них есть общее — модуль. Модуль у противоположных чисел одинаковый: у положительного числа он равен самому числу, а у отрицательного — противоположному, то есть положительному. Например:
- ∣8∣ = 8, ∣-8∣ = 8.
Действительные числа — это числа, которые могут быть записаны в виде конечной или бесконечной десятичной дроби.
Рациональные числа — это числа, которые можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль.
Правило сложения чисел с разными знаками
Положительное число можно рассматривать как доход, а отрицательное — как расходы или долг. Чтобы понять, сколько мы заработали или потратили, нужно смотреть на модули этих чисел.
Например, родители выдали триста рублей на карманные расходы. Если в конце недели у нас осталось немного денег — значит расходов было меньше, чем дохож. А если нам пришлось попросить еще 50 рублей на наклейки — расходы привысили доход. Если же расходы равны доходам, то у нас будет нулевой остаток.
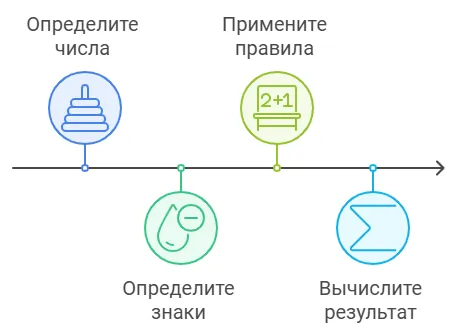
А теперь сформулируем правило сложения чисел с разными знаками.
|
Чтобы сложить положительное и отрицательное число, нужно:
|
Это правило сводит сложение чисел с разными знаками к вычитанию из большего положительного числа меньшее число. В результате сложения положительного и отрицательного числа может получиться: положительное число, отрицательное число или нуль.
Вот, как выглядит эта последовательность на примере 2 + (-6) = -4:
| Знаки слагаемых | Знак суммы | Модули слагаемых | Модуль суммы | Разность модулей слагаемых | Сравнение знака суммы со знаками слагаемых |
| Разные | «−» | ∣2∣ = 2 ∣-6∣ = 6 |
∣-4∣ = 4 | ∣-6∣ - ∣2∣ = 4 6 - 2 = 4 |
Знак результата (-4) такой же, как и у числа, которое больше по модулю (-6) |
Повторим еще раз. Чтобы сложить числа с разными знаками:
- из большего модуля вычесть меньший модуль;
- в результате поставить знак слагаемого с большим модулем.
Алгоритм сложения чисел с разными знаками справедлива для целых чисел, для рациональных чисел и для действительных чисел.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Получи больше пользы от Skysmart:
-
Прокачивай знания на курсах математики.
-
Выбирай из 1200+ репетиторов по математике.
Записывайся на бесплатные курсы для детей.
Примеры сложения чисел с разными знаками
Сложение чисел с разными знаками требует внимательности и последовательности. Рассмотрим примеры по правилу выше:
Пример 1. Сложить числа -8 и 1.
Как решаем:
Нам нужно сложить числа с разными знаками. Выполним все шаги по правилу сложения положительного и отрицательного числа.
- Сначала найдем модули слагаемых, они равны 8 и 1 соответственно.
- Модуль числа -8 больше, чем модуль числа 1. Запомним знак минус.
Теперь от большего модуля отнимаем меньший модуль:
8 - 1 = 7. - Осталось поставить знак минус перед полученным числом, получаем ответ: -7.
На этом сложение чисел с разными знаками завершено.
Ответ: (-8) + 1 = -7.
Пример 2. Сложить положительное число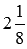 
и отрицательное число -1,25.
Чтобы сложить рациональные числа с разными знаками, которые не являются целыми, их следует представить в виде обыкновенных или десятичных дробей.
Как решаем:
- Представим числа в виде обыкновенных дробей.
Для этого выполним переход от смешанного числа к неправильной дроби:
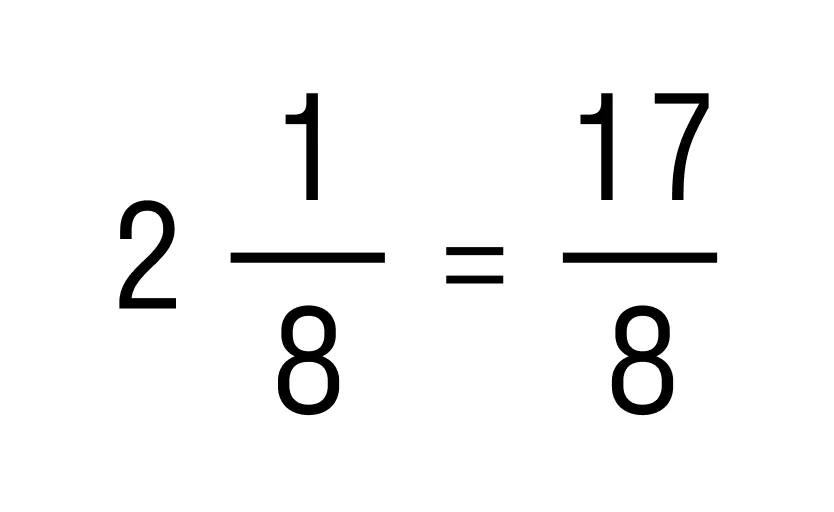, и переводим десятичную дробь в обыкновенную:
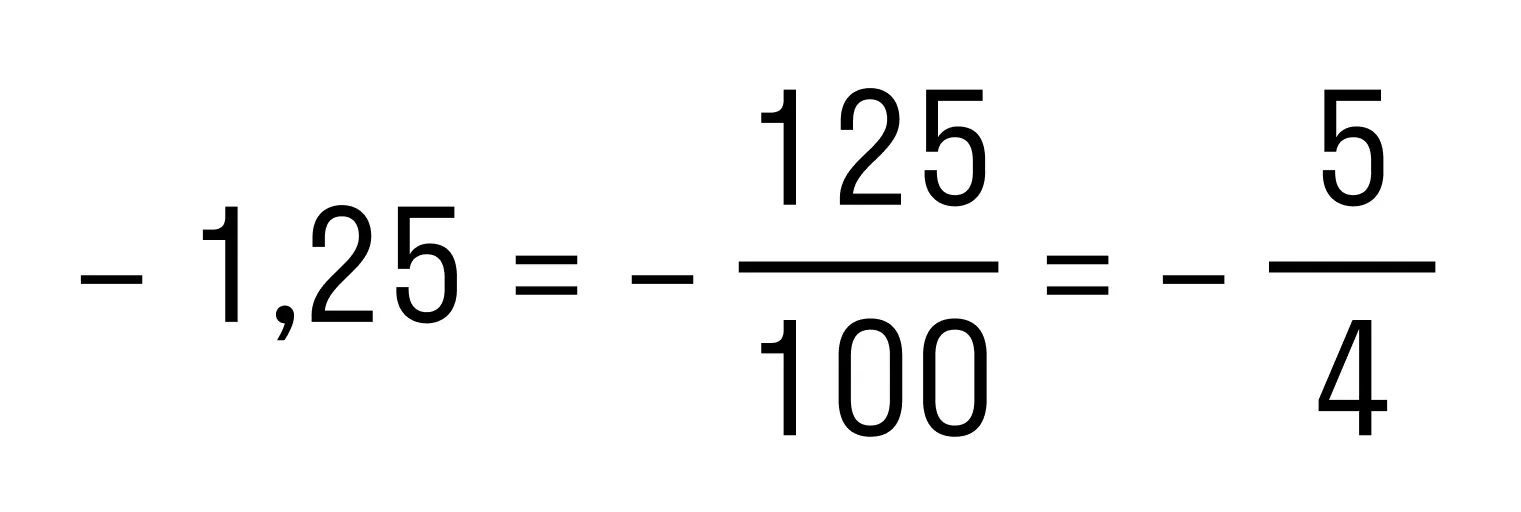
- Теперь можно воспользоваться правилом сложения чисел с разными знаками.
Модули складываемых чисел равны 17/8 и 5/4. Чтобы нам было удобнее считать, приведем дроби к общему знаменателю — получаем 17/8 и 10/8. - Сравним обыкновенные дробей 17/8 и 10/8.
Так как 17>10, то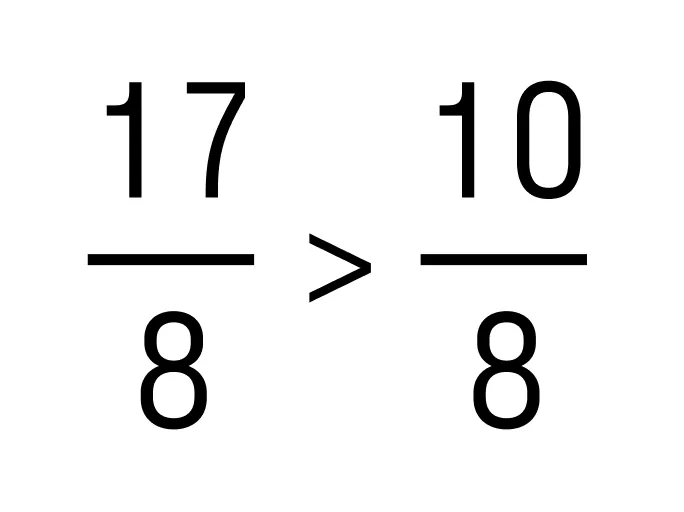
. Это значит, что слагаемое со знаком плюс имеет больший модуль, поэтому запоминаем знак плюс. - Теперь из большего модуля вычитаем меньший, то есть, выполним вычитание дробей с одинаковыми знаменателями:
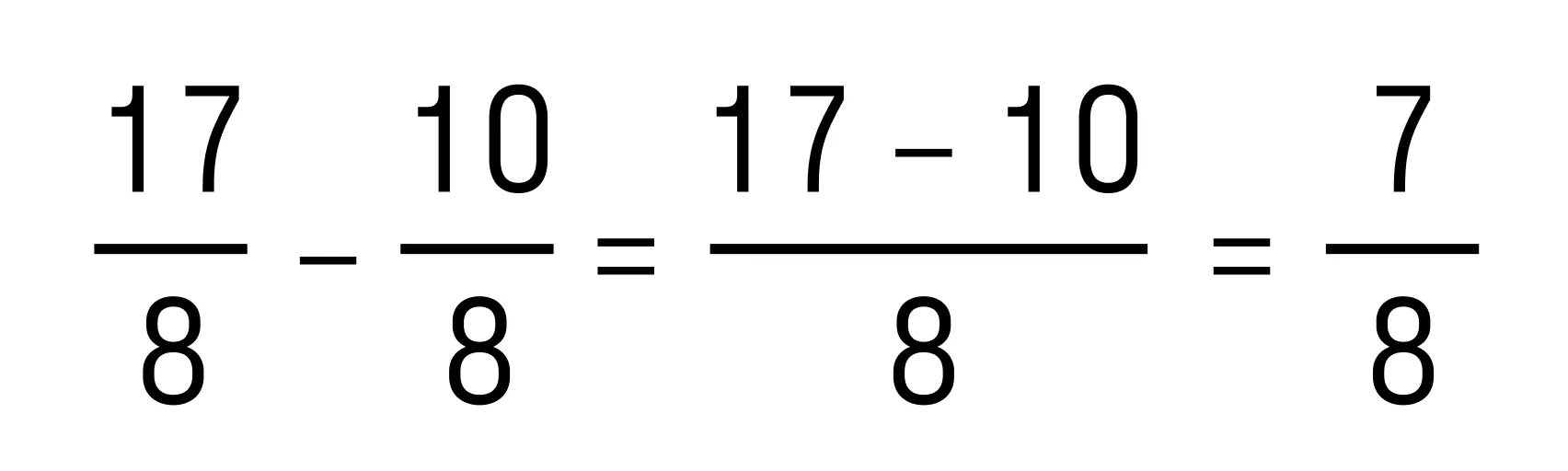
Осталось перед полученным числом поставить знак плюс, получаем:
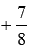, то есть 7/8.
На этом сложение чисел с разными знаками завершено. Краткая запись решения выглядит так:
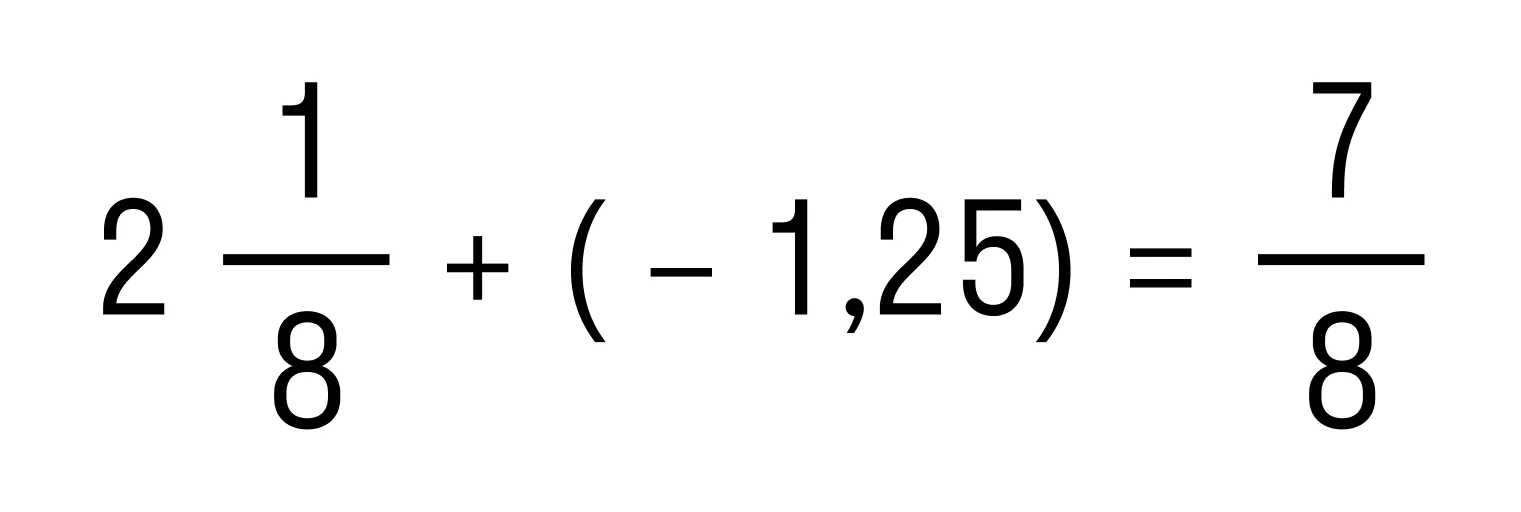
Пример 3. Чему равна сумма чисел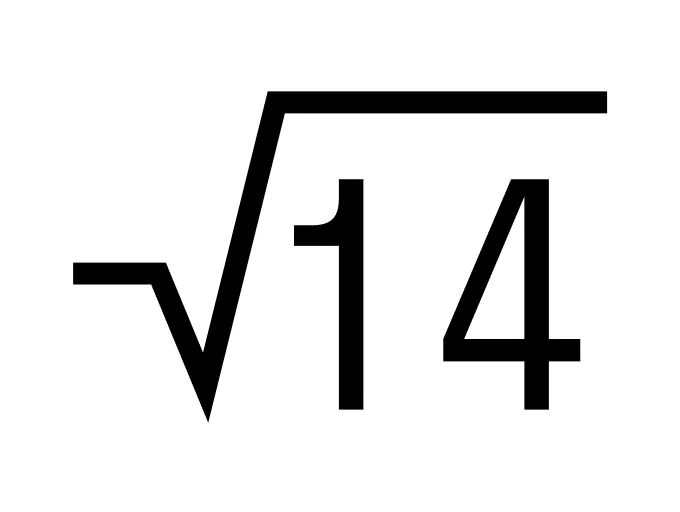 
и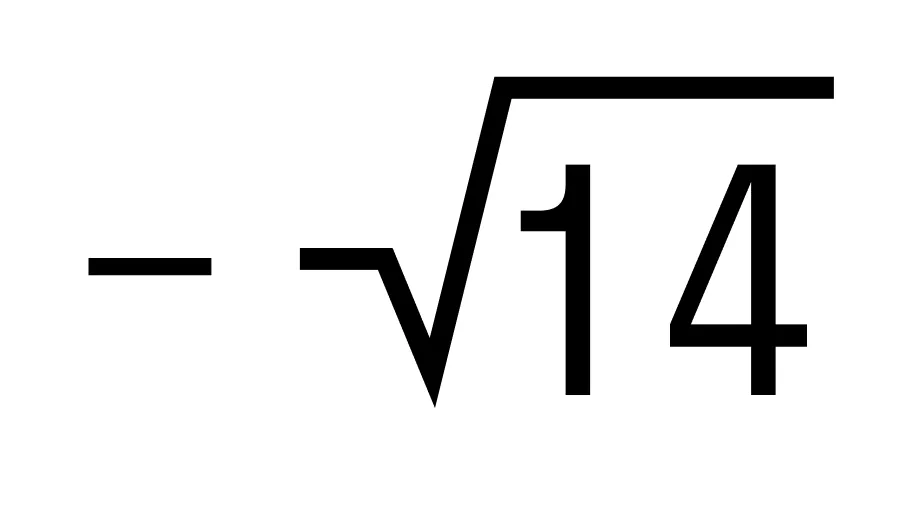 
?
Как решаем:
Замечаем, что у складываемых чисел разные знаки, а их модули равны. Значит эти числа являются противоположными, а сумма противоположных чисел равна нулю.
Получается вот так: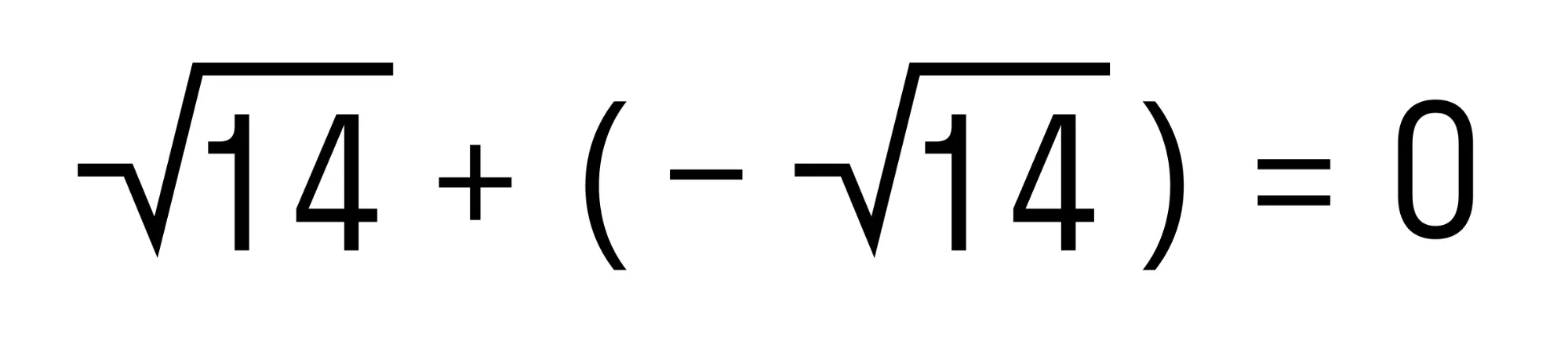 
Ответ: 0.
Важно помнить, что при сложении действительных чисел с разными знаками результат можно записывать не в виде бесконечной десятичной дроби, а в виде числового выражения, которое содержит корни, степени, логарифмы и прочее.
- Например, результат сложения двух чисел с разными знаками -1 и π записывается так: π - 1.
