Уравнение касательной к графику функции

Как составить уравнение касательной к графику функции

Но как поступать, если нужно составить уравнение касательной к графику функции?

Уравнение касательной к графику функции y = f(x) в точке находится по формуле .

Для упрощения понимания этой формулы запишем алгоритм составления уравнения касательной к кривой y = f(x) в точке :

1. Вычислим значение функции в точке касания, для этого подставим в y = f(x) и посчитаем.

2. Продифференцируем функцию y = f(x).

3. Вычислим значение функции в точке касания, для этого подставим в и посчитаем.

4. Составим уравнение касательной и приведем его к виду y = kx + b.

В чем заключается геометрический смысл производной

Одну из главных ролей в записи касательной к графику играет производная, поэтому определим ее геометрический смысл.

Пусть задана произвольная функция y = f(x).

На графике этой функции возьмем точку А с координатами . А теперь выберем точку B с координатами недалеко от точки А.

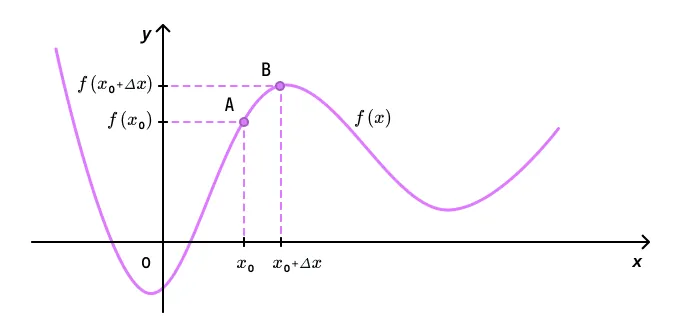
Проведем через точки A и B прямую.

Угол наклона прямой к оси абсцисс обозначим буквой .

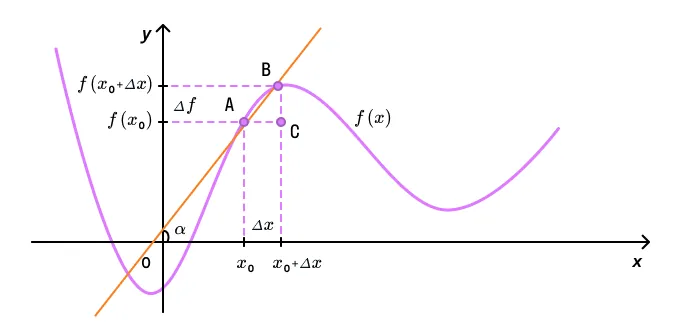
Проведем через точку А прямую, параллельную оси абсцисс, а через точку B — прямую, параллельную оси ординат. Пусть эти две прямые пересекутся в точке C.

Тогда катет , а катет .

Если взять отношения этих значений , то получим отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике ABC, что равно .

Если уменьшать расстояние между точками A и B, то будут уменьшаться длины отрезков и и в какой-то момент точка В совпадет с точкой A, а отношение станет равно производной функции y = f(x) в точке .

Тут может возникнуть вопрос: при чем здесь геометрический смысл производной, если мы начали с касательной?

Касательная — это прямая. Вспомним уравнение прямой: y = kx + b, где k — это коэффициент наклона прямой, и он равен тангенсу угла между прямой и осью абсцисс. А теперь совмещаем все данные и делаем вывод, что .

Это очень важный для нас вывод, попробуем применить его на практике, а именно на задачах формата профильного ЕГЭ по математике.

178.1K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Решение задач

Задача 1

К графику функции y = f(x) проведена касательная в точке с абсциссой . Нужно найти угловой коэффициент касательной к графику данной функции.

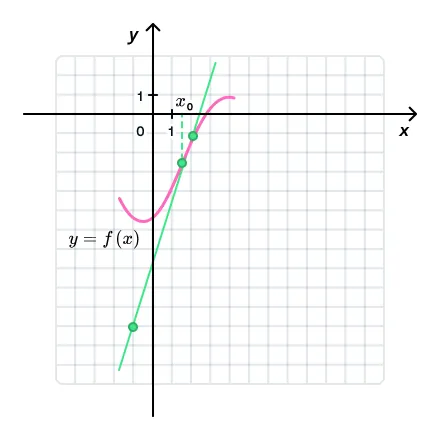
Из теории выше мы узнали, как найти угловой коэффициент касательной — он равен тангенсу угла наклона касательной к графику функции в точке. Значит, через целочисленные точки на прямой построим прямоугольный треугольник и найдем отношение противолежащего катета к прилежащему — получится .

Ответ: 3.

Задача 2

К графику функции y = f(x) проведена касательная в точке с абсциссой . Определите угловой коэффициент касательной в точке .

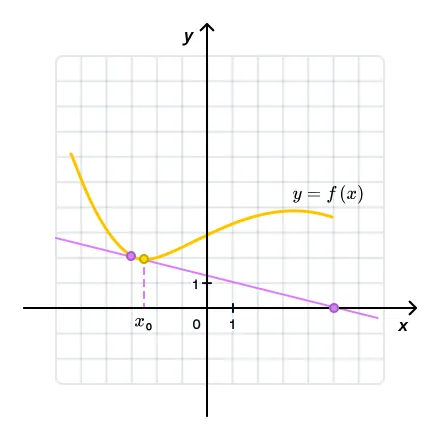
Действуйте по уже известным правилам. Получился ответ 0,25? А вот и нет! В данном случае нужно обратить внимание на убывание графика касательной. Видите, она слева направо идет вниз? Значит, к ответу нужно добавить минус и записать его — получится −0,25.

Ответ: −0,25.

Задача 3

На рисунке изображен график функции y = f(x), определенной на интервале (−8; 3). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 36.

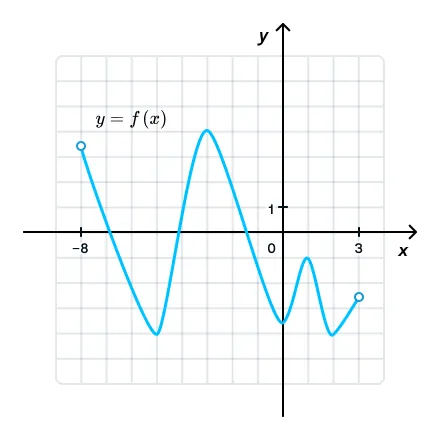
Надеюсь, вы не подумали, что мы будем изображать прямую y = 36 и искать касательные, параллельные ей. 🤯 Достаточно будет рассуждений. Прямая y = 36 — горизонтальная прямая с k = 0, а значит, и у касательных к графику k = 0 или тангенс угла наклона касательной к графику функции также будет равен нулю, что может быть только в точках экстремума функции или, проще говоря, в «бугорках» функции.

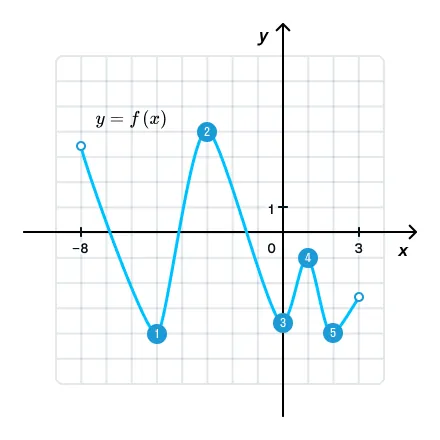
В ответе просили указать количество таких точек, значит, ответ — 5.

Ответ: 5.

Задача 4

Прямая y = 4x + 13 параллельна касательной к графику функции . Найдите абсциссу точки касания.

Если прямая параллельна касательной к графику функции, то у них будут равные угловые коэффициенты. Угловой коэффициент прямой y = 4x + 13 равен 4, а угловой коэффициент касательной к графику функции равен производной от этой функции, то есть 2x − 3. Приравняем полученные значения и найдем x:

2x − 3 = 4;

x = 3,5.

Ответ: 3,5 — абсцисса точки касания.

Задача 5

Запишите уравнение касательной к параболе в точке .

Воспользуемся алгоритмом выше:

1. Вычислим значение функции в точке касания, для этого подставим в и посчитаем: .

2. Продифференцируем функцию: .

3. Вычислим значение функции в точке касания: .

4. Все найденные значения подставим в уравнение касательной: .

5. Приведем полученное выражение к виду y = kx + b: y = −2x + 24.

Ответ: уравнение касательной y = −2x + 24.

По условию задачи нас не просили, но мы можем изобразить график квадратичной функции и касательную к параболе для проверки. Если получилась лишь одна точка касания с правильными координатами, значит, наши расчеты были верны!

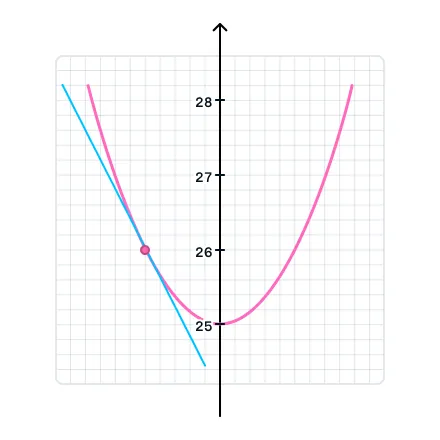
Некоторые темы математики, как клубок ниток, содержат в себе понятия и правила из других тем. Не понимая прошлые темы, не удастся разобраться и в новой. На каждом уроке курсов обучения математике в онлайн-школе Skysmart мы актуализируем уже имеющиеся знания, поэтому не разобраться не получится. Приходите на бесплатный вводный урок за подробным разбором сильных и слабых сторон и конкретными рекомендациями, как улучшить оценки и подготовиться к экзаменам!