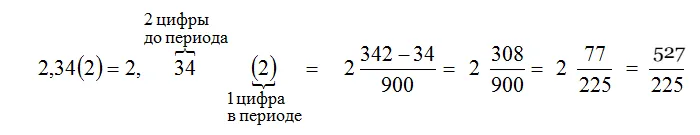Как перевести периодическую дробь

 

Для кого эта статья:

• Студенты и ученики, готовящиеся к экзаменам по математике
• Преподаватели математики, ищущие информацию для уроков
• Любители математики, интересующиеся дробями и их преобразованием

Определение дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математике, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

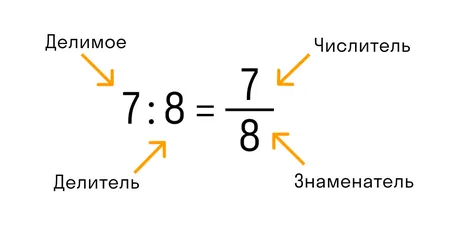
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

• 0,7
• 6,51
• 9,932

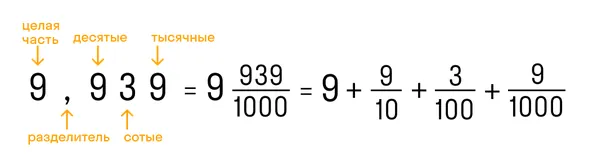
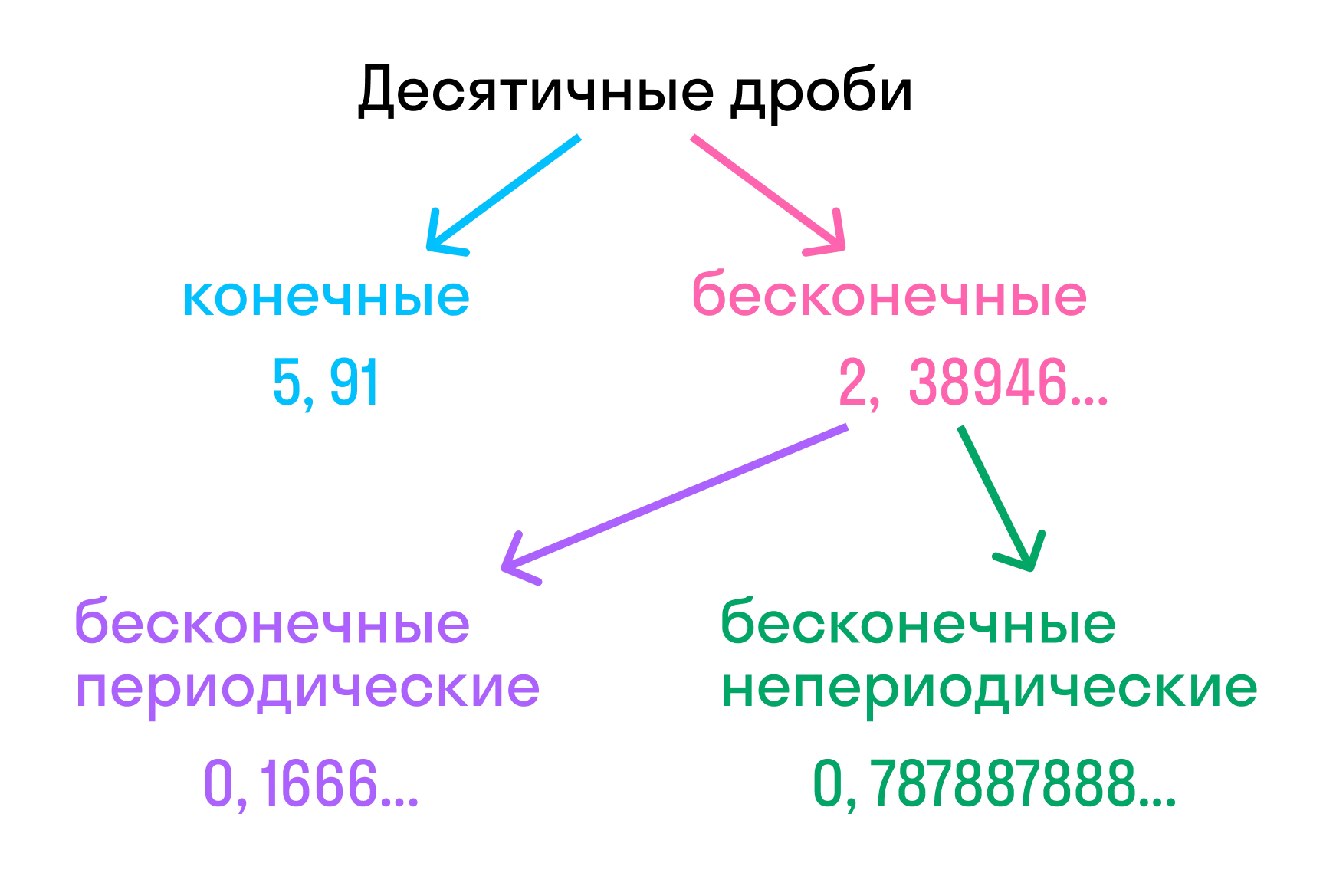
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Переход к периодической десятичной дроби

Рассмотрим обыкновенную дробь вида a/b. Разложим ее знаменатель на простые множители. Тут есть два варианта:

1. В разложении присутствуют только множители 2 и 5. Эти дроби легко приводятся к десятичным.


2. В разложении присутствует что-то еще, кроме 2 и 5. В этом случае дробь невозможно представить в виде десятичной, зато из нее можно сделать периодическую десятичную дробь.

 

Чтобы задать периодическую десятичную дробь, нужно найти ее периодическую и непериодическую часть. Чтобы это сделать нужно привести дробь в неправильную, а затем разделить числитель на знаменатель столбиком.

Что будет происходить в процессе:

• сначала нужно будет разделить целую часть, если она есть;
• могут быть несколько чисел после десятичной точки;
• через некоторое время цифры начнут повторяться.

Повторяющиеся цифры после десятичной точки нужно обозначить периодической частью, а то, что стоит спереди — непериодической.

Пример. Перевести обыкновенные дроби в периодические десятичные:

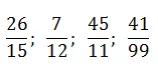
Как решаем:

Все дроби без целой части, поэтому просто делим числитель на знаменатель уголком:

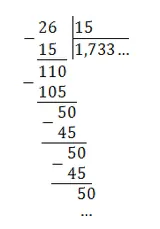
Остатки начали повторяться. Запишем дробь в соответствии с условиями задачи: 1,733 ... = 1,7(3).

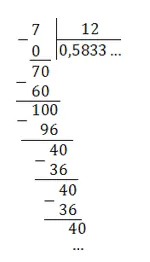
В итоге получаем: 0,5833 ... = 0,58(3).

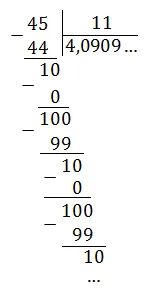
Фиксируем: 4,0909 ... = 4,(09).

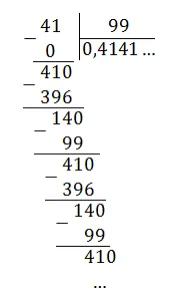
Получаем десятичную периодическую дробь: 0,4141 ... = 0,(41).

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

206.7K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Прокачивай знания на курсах математики

• Выбирай из 1200+ репетиторов по математике

• Записывайся на бесплатные курсы для детей

Определение периодической дроби

Периодическая дробь — это бесконечная десятичная дробь, в которой, начиная с некоторого места, периодически повторяется определенная группа цифр.

Периодическая часть дроби — это набор повторяющихся цифр, из которых состоит значащая часть.

В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».

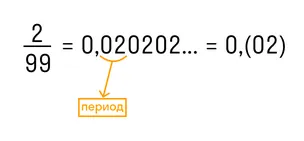
Остальной отрезок значащей части, который не повторяется, называется непериодической частью.

Виды периодических дробей: чистые и смешанные.

Чистая периодическая десятичная дробь — это десятичная дробь, в записи которой сразу после запятой следует период. Например: 1,(4); 4,(25); 21,(693).

Смешанная периодическая десятичная дробь — это десятичная дробь, в записи которой после запятой через одну или несколько цифр начинается период. Например: 3,5(1); 0,02(89); 7,0(123) и т.д.

Рассмотрим примеры дробей, чтобы научиться определять части и период.

1/3 = 0,3333... = 0,(3)

Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.

Читаем так: ноль целых три в периоде.

7/12 = 0,583333... = 0,58(3)

Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.

Читаем так: ноль целых пятьдесят восемь сотых и три в периоде.

17/11 = 1,545454... = 1,(54)

Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.

Читаем так: одна целая пятьдесят четыре сотых в периоде.

25/39 = 0,641025 641025... = 0,(641025)

Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6.

Читаем так: ноль целых шестьсот сорок одна двадцать пять миллионных в периоде.

пятьдесят четыре сотых в периоде.

9200/3 = 3066,666... = 3066,(6)

Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.

Читаем так: три тысячи шестьдесят шесть целых и шесть в периоде.

 

Перевод периодической дроби в обыкновенную

Давайте разберемся, как перевести периодическую десятичную дробь в обыкновенную дробь.

Если период дроби равен нулю, значит решение будет быстрым. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.

Пример. Преобразуем периодическую дробь 1,32(0) в обыкновенную.

Для этого отбросим нули справа и получим конечную десятичную дробь 1,32. Далее следуем алгоритму из предыдущих пунктов:

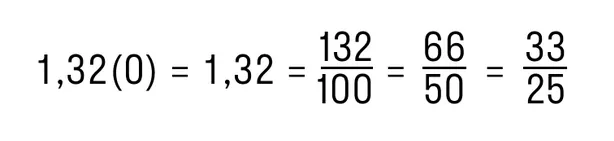
Вот и ответ!

Рассмотрим пример, в котором период дроби отличен от нуля.

Как записать периодическую дробь 10,0219(37) в виде обыкновенной:

1. Считаем количество цифр в периоде десятичной дроби. Обозначаем количество цифр за букву k.

   В нашем примере k = 2.



2. Считаем количество цифр, которые стоят после запятой, но до периода десятичной дроби. Обозначаем количество цифр буквой m.

   m = 4.



3. Запишем все цифры после запятой: в том числе и цифры из периода в виде натурального числа.

   Если вначале, до первой значащей цифры, идут нули, то отбрасываем их. Обозначим полученное число — a.

   a = 021937 = 21 937



4. Теперь запишем все цифры, которые стоят после запятой, но до периода, в виде натурального числа. Если вначале до первой значащей цифры идут нули, то отбрасываем их. Обозначим полученное число — b.

   b = 0219 = 219



5. Подставляем найденные значения в формулу, где Y — целая часть бесконечной периодической дроби.

   Y = 10

   
   


6.  

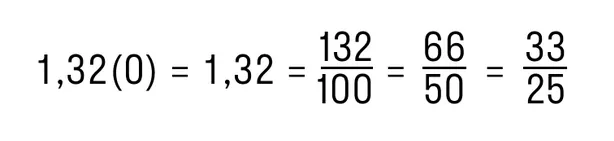
Теперь осталось подставить все найденные значения в формулу и получить ответ:

Вот так мы справились с задачей представить бесконечную периодическую дробь в виде обыкновенной.

Есть еще один способ преобразовать периодическую дробь в обыкновенную. Для этого нужно рассматреть периодическую часть как сумму членов геометрический прогрессии, которая убывает. Например, вот так:

0,(98) = 0,98 + 0,0098 + 0,000098 + 0,00000098 + ..

Для суммы членов бесконечной убывающей геометрической прогрессии есть формула. Если первый член прогрессии равен b, а знаменатель q таков, что 0 < q < 1, то сумма равна b/(1-q).

Пример. Перевести периодическую дробь 0,(7) в обыкновенную.

Как решаем:

1. Запишем 0,(7) = 0,7 + 0,07 + 0,007 + ..

   Видим бесконечную убывающую геометрическую прогрессию с первым членом 0,7 и знаменателем 0,1.



2. Применим формулу b/(1-q):

   0,(7) = 0,7 + 0,07 + 0,007 + .. = 0,7 / (1 - 0,1) = 0,7/0,9 = 7/9.



3.  

Ответ: 7/9.

Итак, есть два вида периодических дробей. Сейчас расскажем, чем отличаются способы их преобразования в обыкновенные дроби.

Перевод чистой периодической дроби в обыкновенную

Напомним: отличие чистой периодической десятичной дроби в том, что в ней сразу после запятой следует период.

Чтобы обратить чистую периодическую дробь в обыкновенную, достаточно записать числителем ее период, а в знаменателе записать столько девяток, сколько цифр в периоде. Вот так:

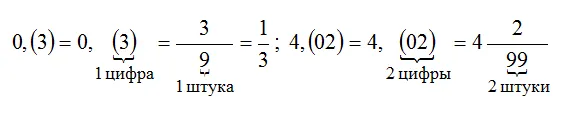
Перевод смешанной периодической дроби в обыкновенную

Отличие смешанной периодической десятичной дроби в том, что после запятой через одну или несколько цифр начинается период.

Чтобы записать смешанную периодическую дробь в виде обыкновенной, нужно из числа, которое стоит до второго периода вычесть число, стоящее до первого периода, и записать результат в числителе.

А в знаменатель нужно поставить число, которое содержит столько девяток, сколько цифр в периоде, нулей в конце и сколько цифр между запятой и периодом.

Например, запишем 2,34(2) в виде обыкновенной дроби: