Практикуйся по этой теме! Пройди задание №14 ЕГЭ по базовой математике |
Сложение и вычитание десятичных дробей - это арифметические операции, при которых числа с дробной частью приводятся к общему знаменателю. Примеры:
- 1) 1.23 + 3.45 = 4.68
- 2) 5.67 - 2.34 = 3.33
Правило: записать числа друг под другом так, чтобы запятая была под запятой, выполнить операцию, поставить в ответе запятую под запятой.
Понятие десятичной дроби
Прежде, чем перейдем к тому, как выполнить сложение и вычитание десятичных дробей, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это число в математике, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
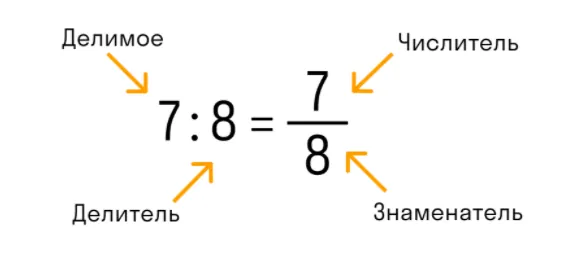
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Ее записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,8
- 7,42
- 9,932
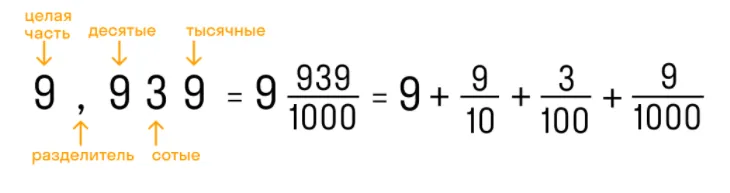
Конечная десятичная дробь — это когда количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т. д.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Получи больше пользы от Skysmart:
-
Прокачивай знания на курсах математики.
-
Выбирай из 1200+ репетиторов по математике.
Записывайся на бесплатные курсы для детей.
Сложение десятичных дробей
Мы знаем, что десятичная дробь состоит из целой и дробной части. При сложении десятичных дробей нужно отдельно сложить каждую часть.
Рассмотрим пример сложения 3,2 и 5,3. Для удобства используем метод столбика.
Запишем эти две дроби в столбик. При этом целая часть одной дроби должна быть под целой частью другой. В школе это называют «запятая под запятой». Вот так:
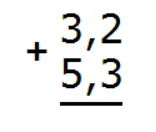
Складываем дробные части: 2 + 3 = 5. Запишем пятерку в дробной части ответа:
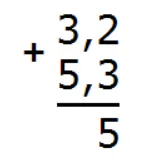
Теперь целые части: 3 + 5 = 8. Запишем восьмерку в целой части ответа:
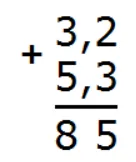
Отделим запятой целую часть от дробной, чтобы запятая была под запятой:
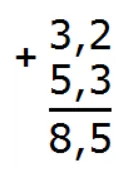
Получили ответ: 3,2 + 5,3 = 8,5.
Вычитание десятичных дробей
Процесс вычитания десятичных дробей очень похож на сложение. Будем использовать те же правила: «запятая под запятой» и «равное количество цифр после запятой».
Пример 1. Найти значение выражения 2,5 − 2,2
Запишем в столбик выражение так, чтобы запятая была под запятой:
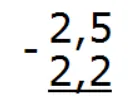
Вычислим дробную часть 5 − 2 = 3. Запишем тройку в десятой части ответа:
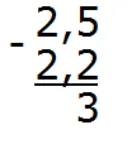
Вычислим целую часть 2 − 2 = 0. Запишем ноль в целой части ответа:
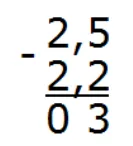
Отделим запятой целую часть от дробной:
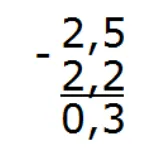
Вот и ответ: 2,5 − 2,2 = 0,3.
Пример 2. Вычислить: 7,353 – 3,1
В этом выражении разное количество цифр после запятой: в 7,353 три цифры после запятой, а в 3,1 только одна. Значит в дроби 3,1 в конце добавим два нуля, чтобы уравнять количество цифр в обеих дробях. То есть: 3,1 = 3,100.
Запишем в столбик и посчитаем:
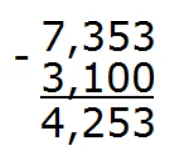
Ответ: 7,353 – 3,1 = 4,253.
Пример 3. Вычислить: 3 − 1,2
В этом примере из целого числа нужно вычесть десятичную дробь. Запишем это выражение столбиком так, чтобы целая часть десятичной дроби 1,23 была под числом 3. Вот так:
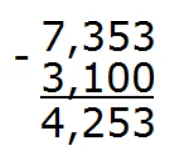
Сделаем количество цифр после запятой одинаковым:
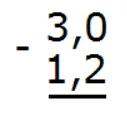
Теперь вычитаем десятые части: 0 − 2. От нуля невозможно вычесть число 2. Поэтому займем единицу у соседнего разряда. Таким образом 0 превращается в число 10. Вычисляем десятые части: 10 − 2 = 8. Запишем восьмерку в десятой части ответа:
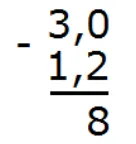
Сейчас вычтем целые части. В самом начале было число 3, но мы заняли у него единицу, поэтому оно обратилось в двойку. Поэтому: 2 − 1 = 1. Запишем единицу в целой части ответа:
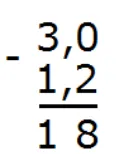
Отделим запятой целую часть от дробной:
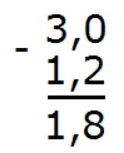
Ответ: 3 − 1,2 = 1,8.
Мы рассмотрели несколько примеров сложения и вычитания десятичных дробей. Чтобы каждый ученик в 5 и 6 классе мог повторить эту последовательность, есть специальный алгоритм:
|
Алгоритм сложения (вычитания) десятичных дробей
|
Проще говоря, правило сложения (вычитания) десятичных дробей звучит так: чтобы сложить (вычесть) две десятичные дроби, нужно записать их в столбик друг под другом, запятая под запятой. А потом сложить (вычесть) как обыкновенные числа и снести запятую.
