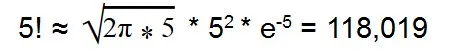Формула факториала — это формула для вычисления произведения всех натуральных чисел от 1 до данной. Обозначается как n! и определяется как n! = n × (n - 1)!. Например, 5! = 5 × 4 × 3 × 2 × 1 = 120.
Факториал: определение
Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».
Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:
- -3,75! 2,23! -2!
Число должно быть целое и положительное:
- 3! 56! 12!
| Формула факториала n!=1⋅2⋅3⋅...⋅(n−2)⋅(n−1)⋅n |
Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.
Например:
- 3! = 1*2*3 = 6
- 4! = 1*2*3*4 = 24
- 5! = 1*2*3*4*5 = 120
- 6! = 1*2*3*4*5*6 = 720
Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6
Формулы и свойства факториала
Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.
| 1! = 1 |
| 2! = 2 |
| 3! = 6 |
| 4! = 24 |
| 5! = 120 |
| 6! = 720 |
| 7! = 5040 |
| 8! = 40320 |
| 9! = 362880 |
| 10! = 3628800 |
| 11! = 39916800 |
| 12! = 479001600 |
| 13! = 6227020800 |
| 14! = 87178291200 |
| 15! = 1307674368000 |
| 16! = 20922789888000 |
| 17! = 355687428096000 |
| 18! = 6402373705728000 |
| 19! = 121645100408832000 |
| 20! = 2432902008176640000 |
| 21! = 51090942171709440000 |
| 22! = 1124000727777607680000 |
| 23! = 25852016738884976640000 |
| 24! = 620448401733239439360000 |
| 25! = 15511210043330985984000000 |
Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:
- (n - 1)! = 1*2*3*4*5*...*(n - 2)(n - 1)
- n! = 1*2*3*4*5*...*(n - 2)(n - 1)n
- (n + 1)! = 1*2*3*4*5*...*(n - 2)(n - 1)n(n + 1)
С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.
Такая формула дает результат с небольшой погрешностью.
 |
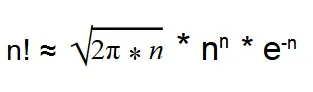Пример:
Рекуррентная формула
 |
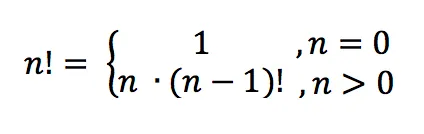Примеры:
- 5! = 5*(5 - 1)! = 5*4! = 5*24 = 120
- 6! = 6*(6-1)! = 6*5! = 6*120 = 720
Для решения примеров обращайтесь к таблице.
Примеры умножения факториалов:
- Пользуйтесь готовой таблицей 5! * 7! = 120 * 5040 = 604800
- Или раскладывайте факториалы отдельно, если хотите потренироваться:
5! = 1*2*3*4*5 = 4! * 5 =120
7! = 1*2*3*4*5*6*7 = 6! * 7 = 5040
120 * 5040 = 604800
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Получи больше пользы от Skysmart:
-
Подготовься к ОГЭ на пятёрку.
-
Подготовься к ЕГЭ на высокие баллы.
Записывайся на бесплатные курсы для детей.
Решай задания в бесплатном тренажёре ЕГЭ.
Примеры решений
Давайте поупражняемся и решим пару примеров.
1. Сократите дробь:
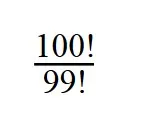
Как решаем:
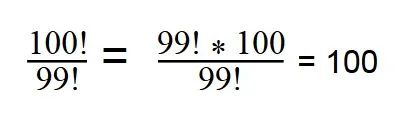
При сокращении факториалов, пользуйтесь свойством:
n! = (n - 1)! * n
100! = 99! * 100
Далее сокращаем по принципу сокращения обыкновенных дробей.
2. Вычислите значение выражения с факториалом: 8! + 5!
Как решаем:
Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.
А можно потренироваться и разложить их:
8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440
3. Вычислите значение выражения:
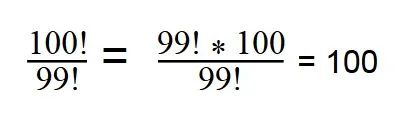
Как решаем:
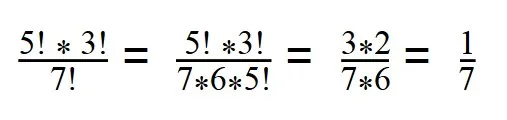
7! = 1*2*3*4*5*6*7 = 5! * 6 *7
Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.
4. Вычислите значение выражение:
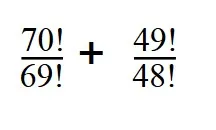
Как решаем:
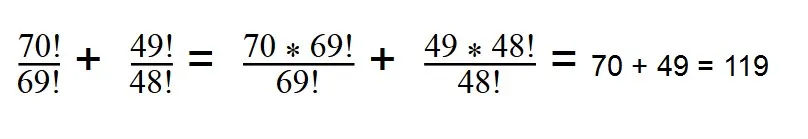
Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*.....*69 = 69! * 70
49! = 1*2*3*....49! * 48
Далее сокращаем все одинаковые множители.
5. Сократите дробь:
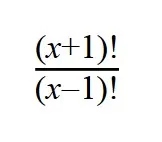
Как решаем:
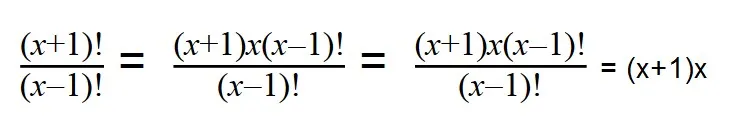
Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.
Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.
