Метод интервалов, решение неравенств

Для кого эта статья:

• Студенты и школьники, готовящиеся к экзаменам по математике
• Преподаватели математики, ищущие методы объяснения неравенств
• Самоучки, заинтересованные в углублённом изучении алгебры и неравенств

Определение квадратного неравенства

Неравенство — алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.

Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти множество, для которых оно выполняется.

Квадратное неравенство выглядит так:

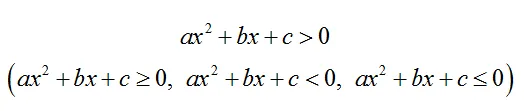
где x — переменная,

a, b, c — числа,

при этом а ≠ 0.

Квадратное неравенство можно решить двумя способами:

• графический метод;
• метод интервалов.

Соглашаюсь на обработку персональных данных в соответствии с условиями пользовательского соглашения

← Далее →

Записаться

Решение неравенства графическим методом

При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax² + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.

Как дискриминант влияет на корни уравнения:

1. D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
2. D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два различных корня;
3. D < 0. Если дискриминант меньше нуля, тогда у квадратного уравнения нет корней.

В зависимости от полученных корней и знака коэффициента a, возможно одно из шести расположений графика функции у = ax² + bx + c.

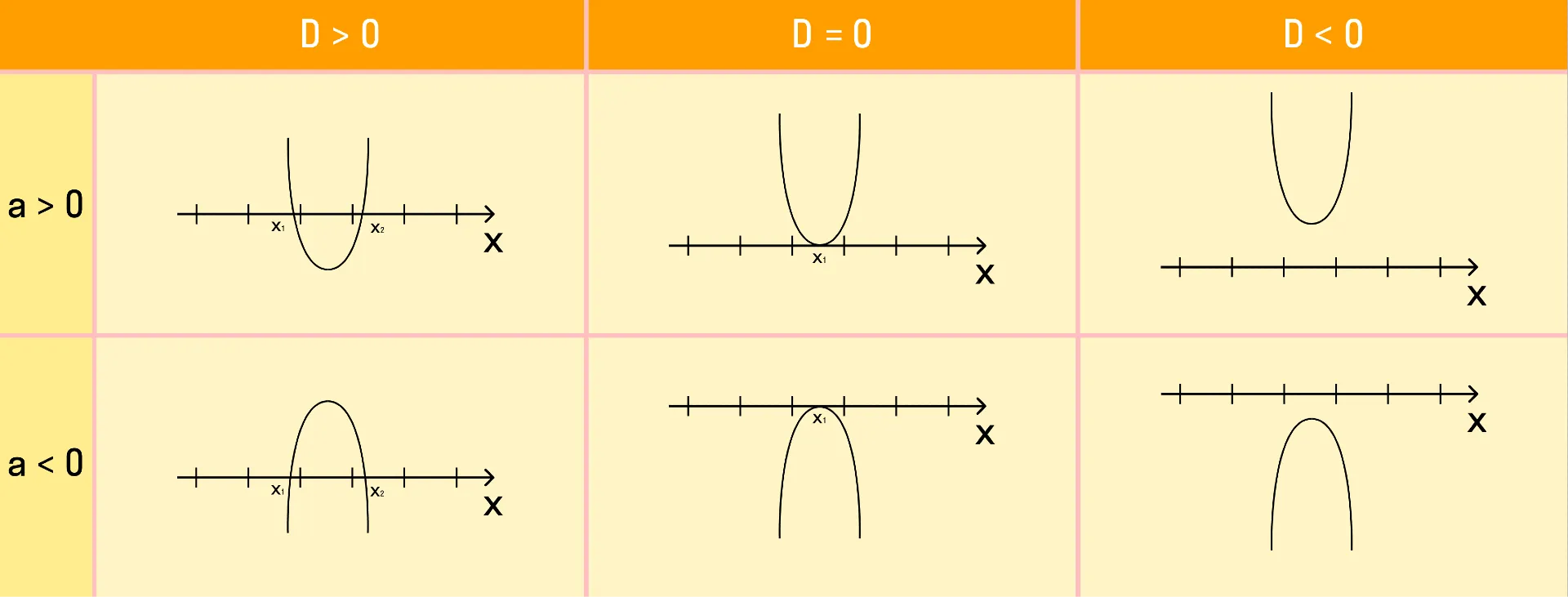
Если требуется найти числовой промежуток, на котором квадратный трехчлен ax² + bx + c больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.

Если нужно найти числовой промежуток, на котором квадратный трехчлен ax² + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.

Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.

Обучение на курсах по математике в онлайн-школе Skysmart сделает сложные темы понятными, а высокий балл на экзаменах — достижимым!

222.4K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку

• Подготовься к ЕГЭ на высокие баллы

• Записывайся на бесплатные курсы для детей

• Решай задания в бесплатном тренажёре ЕГЭ

Решение неравенства методом интервалов

Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.

Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, <, ≤, ≥.

Сейчас мы узнаем про интервалы в контексте решения квадратных неравенств.

Интервал — это некий промежуток числовой прямой, то есть все возможные числа, заключенные между двумя числами — концами интервала. Представить эти промежутки не так просто, поэтому интервалы принято рисовать.

Алгоритм решения квадратных неравенств методом интервалов:

1. Найти нули квадратного трехчлена ax² + bx + c из левой части квадратного неравенства.
2. Изобразить координатную прямую и при наличии корней отметить их на ней.

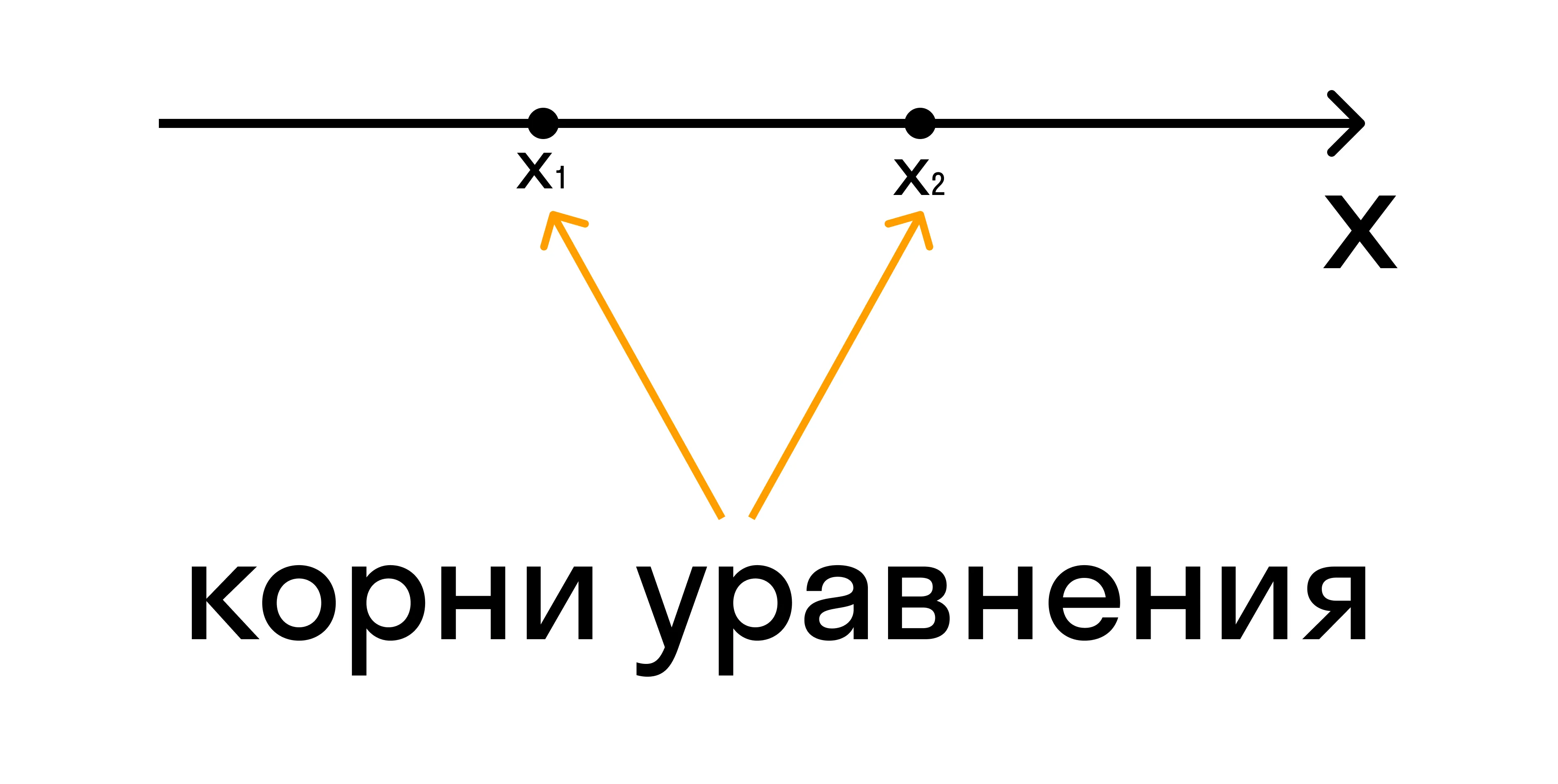
   Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками. Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.

   
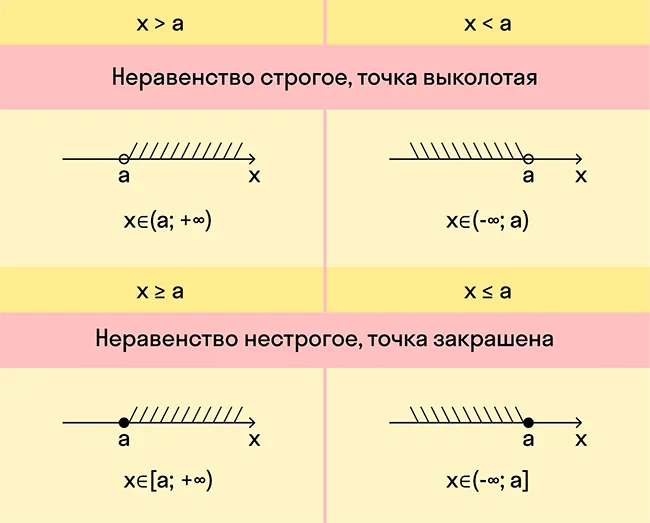
3. Определить, какие знаки имеют значения трехчлена на каждом промежутке (если на первом шаге нашли нули) или на всей числовой прямой (если нулей нет). И проставить над этими промежутками + или − в соответствии с определенными знаками.
4. Если квадратное неравенство со знаком > или ≥ — наносим штриховку над промежутками со знаками +.

   Если неравенство со знаком < или ≤, то наносим штриховку над промежутками со знаком −.

   В результате получаем геометрический образ некоторого числового множества — это и есть решение неравенства.

   Либо вместо штриховки можно нарисовать «арки» для интервалов. Справа налево, начиная с +, проставить чередуя знаки + и −.

   
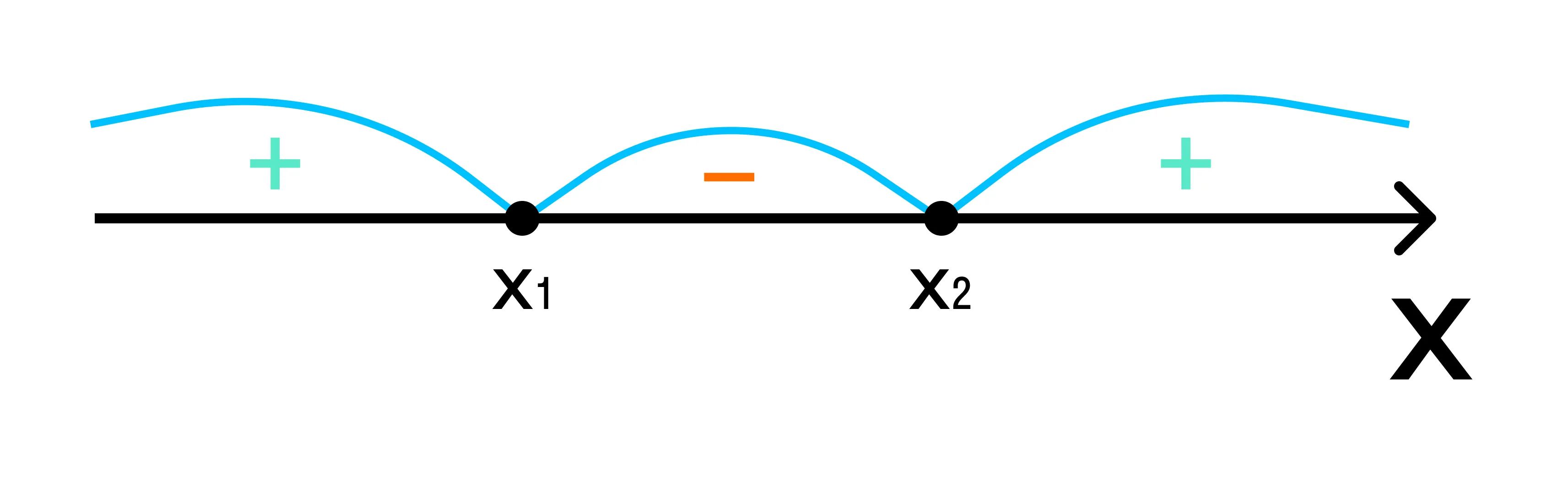
5. Выбрать необходимые интервалы и записать ответ.

Расскажем подробнее про третий шаг алгоритма. Существует несколько подходов для определения знаков на промежутках.

Для примера возьмем трехчлен x² + 4x - 5, его корнями являются числа -5 и 1, они разбивают числовую ось на три промежутка: (-∞, -5), (-5, 1) и (1, +∞).

Определим знак трехчлена x² + 4x - 5 на промежутке (1, +∞). Для этого вычислим значение данного трехчлена при некотором значении x из этого промежутка. Можно брать любое значение переменной, главное — чтобы вычисления были простыми. В нашем случае, возьмем x = 2. Подставим его в трехчлен вместо переменной x:

• 2² + 4 * 2 - 5 = 4 + 8 - 5 = 7.

7 — положительное число. Это значит, что любое значение квадратного трехчлена на интервале (1, +∞) будет положительным. Так мы определили знак плюс.

Определим знаки на оставшихся двух промежутках. Начнем с интервала (-5, 1). Из этого интервала можем взять x = 0 и вычислить значение квадратного трехчлена при этом значении переменной:

• 0² + 4 * 0 - 5 = 0 + 0 - 5 = -5.

Так как -5 — отрицательное число, то на этом интервале все значения трехчлена будут отрицательными. Так мы определили знак минус.

Осталось определиться со знаком на промежутке (-∞, -5). Возьмем x = -6, подставляем:

• (-6)² + 4 * (-6) - 5 = 36 - 24 - 5 = 7.

Следовательно, искомый знак — плюс.

Можно расставить знаки быстрее, если запомнить эти факты:

Плюс или минус: как определить знаки

Можно сделать вывод о знаках по значению старшего коэффициента a:

если a > 0, последовательность знаков: +, −, +,

если a < 0, последовательность знаков: −, +, −.

Можно также сделать вывод о знаках по значению старшего коэффициента a:

если a > 0, последовательность знаков: +, +,

если a < 0, последовательность знаков: −, −.

Например -4x² - 7 не имеет корней и на промежутке (−∞, +∞) его значения отрицательны, так как коэффициент при x² есть отрицательное число -4, и свободный член -7 тоже отрицателен.

• Когда квадратный трехчлен при D > 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
• Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.
• Когда квадратный трехчлен корней не имеет (D < 0), то знаки его значений на всей числовой прямой совпадают как со знаком старшего коэффициента a, так и со знаком свободного члена c.

Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.

Пример 1. Решить неравенство методом интервалов: x^2 - 5x + 6 ≥ 0.

Как решаем:

1. Приравняем квадратный трехчлен к 0 и найдем нули: x² - 5x + 6 = 0 (x - 3) (x -2) = 0 x - 3 = 0 x - 2 = 0 x = 3 x = 2

2. Отметим полученные значения на числовой прямой:

   

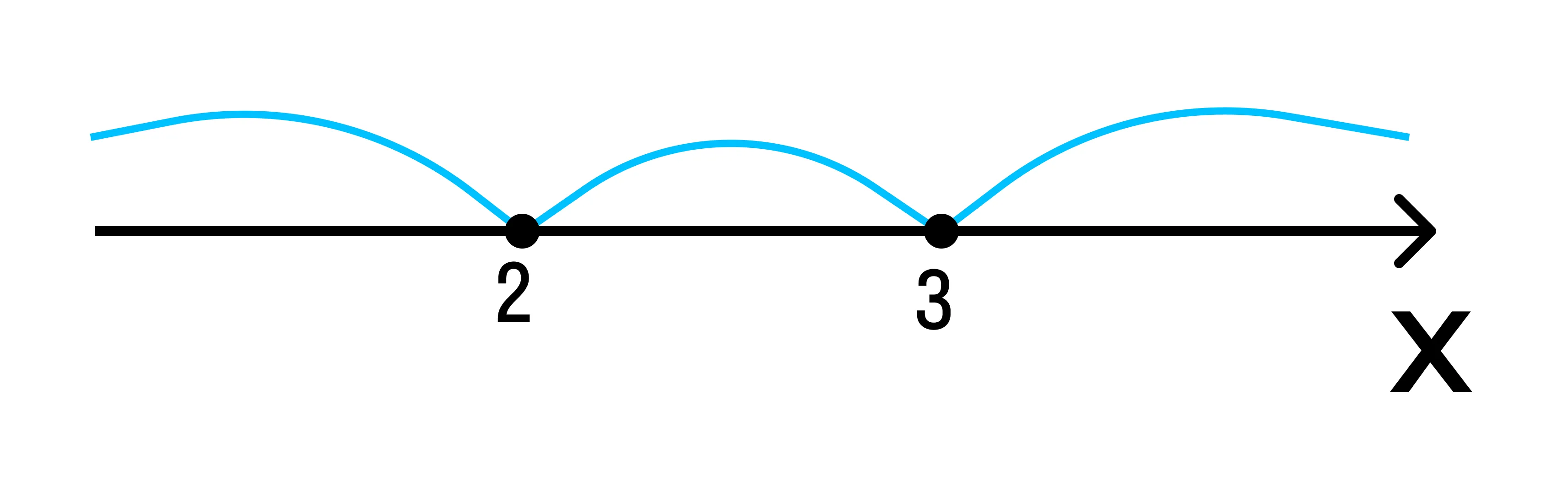
3. Расставим знаки на полученных промежутках:

   

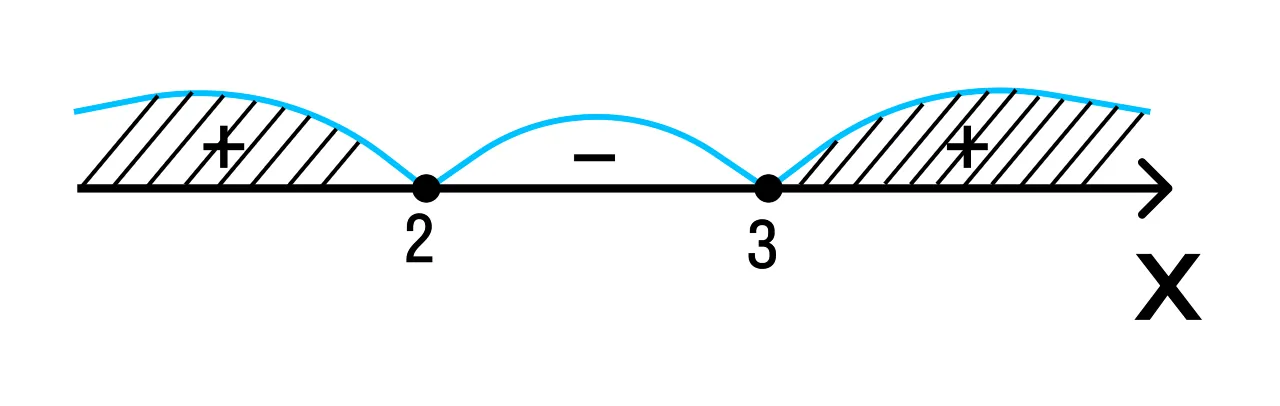
Ответ: х ≤ 2, х ≥ 3.

Пример 2. Применить метод интервалов для решения неравенства x² + 4x + 3 < 0.

Как решаем:

1. Представим левую часть неравенства в виде произведения множителей. Найдем корни соответствующего уравнения x² + 4x + 3 = 0:

   a = 1, b = 4, c = 3
   D = b² − 4ac = 16 − 12 = 4
   x₁ = (−b + √D)/2a = (−4 + 2)/2 = −1
   x₂ = (−b − √D)/2a = (−4 − 2)/2 = −3

   Тогда x² + 4x + 3 = (x + 1) (x + 3)

2. Отметим на числовой прямой корни x₁ = −3 и x₂ = −1. Они разбивают числовую прямую на три интервала: (−∞; −3), (−3; −1), (−1; +∞).

   

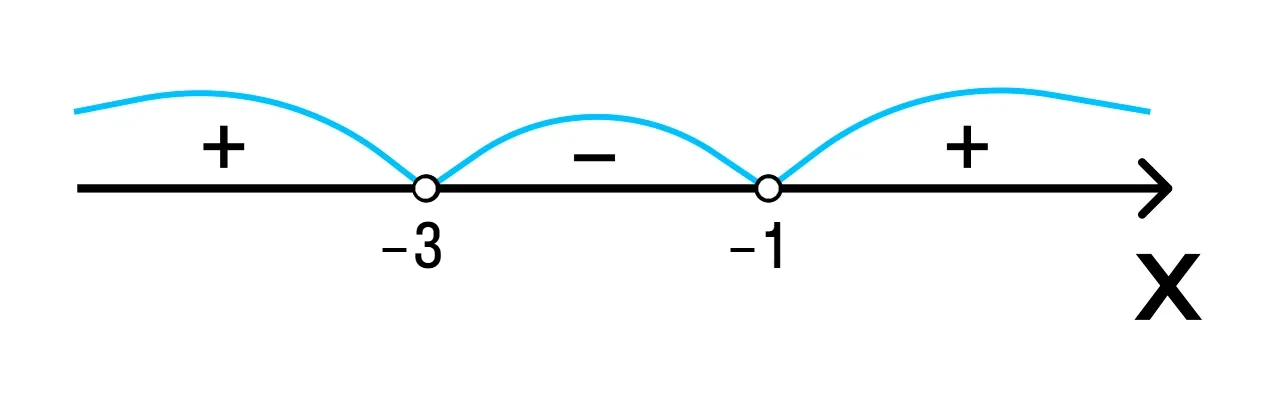
3. Определим знак выражения (x + 1) (x + 3) на каждом интервале.

   • Интервал (-∞; -3):

     Если x < −3, то x + 3 < 0 и x + 1 < 0

     Значит, произведение (x + 1) (x + 3) > 0 (произведение двух отрицательных чисел положительно)

   • Интервал (−3; −1):

     Если −3 < x < −1, то x + 3 > 0 и x + 1 < 0

     Значит, произведение (x + 1) (x + 3) > 0 (произведение чисел с разными знаками отрицательно)

   • Интервал (−1; +∞):

     Если x > −1, то x + 3 > 0 и x + 1 > 0

     Значит, произведение (x + 1) (x + 3) > 0 (произведение двух положительных чисел положительно)

4. Так как нам нужно решить неравенство x² + 4x + 3 < 0, нас интересуют те интервалы, где выражение отрицательно. Это интервал (−3; −1).

Ответ: (−3; −1).

Пример 3. Выполнить решение квадратного неравенства методом интервалов:

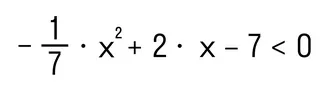
Как решаем:

1. Находим корни квадратного трехчлена, который находится в левой части:
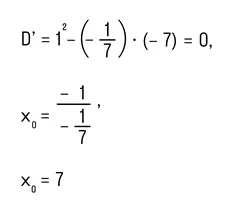
2. Так как мы решаем строгое неравенство, то на координатной прямой изображаем выколотую точку с координатой 7:
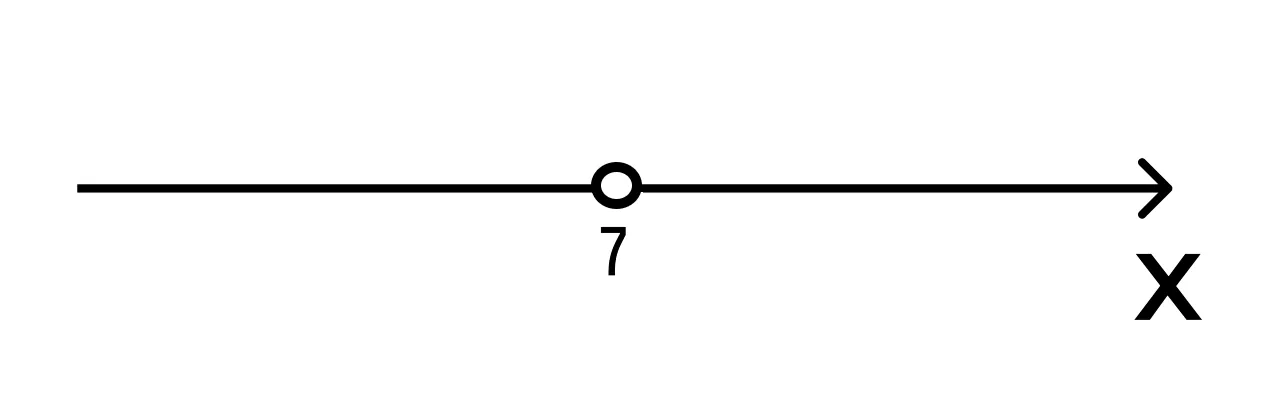
3. Теперь определим знаки на двух полученных промежутках (−∞, 7) и (7, +∞).

   Это легко сделать, потому что дискриминант квадратного трехчлена равен нулю, а старший коэффициент со знаком минус. Фиксируем знаки: −, −:

   
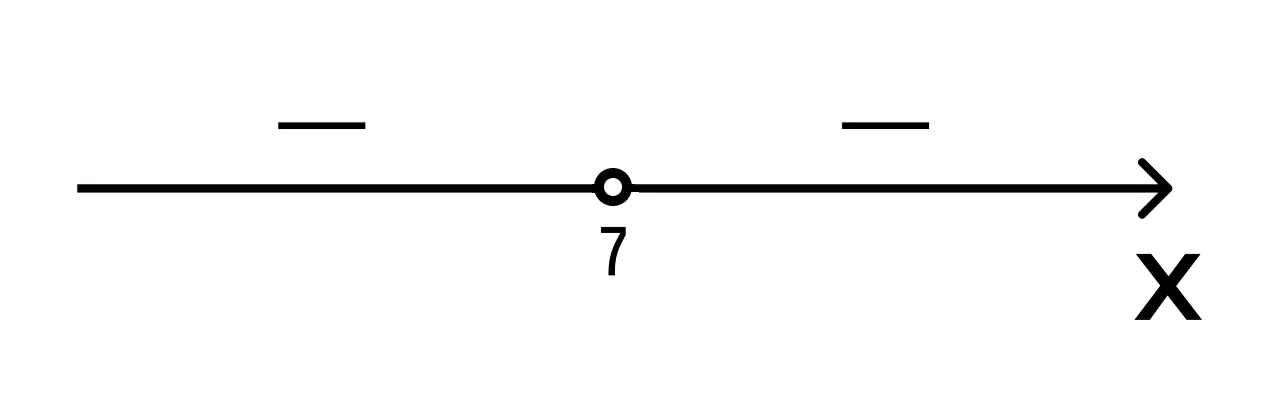
4. Так как мы решаем неравенство со знаком <, то изобразим штриховку над интервалами со знаками минус:

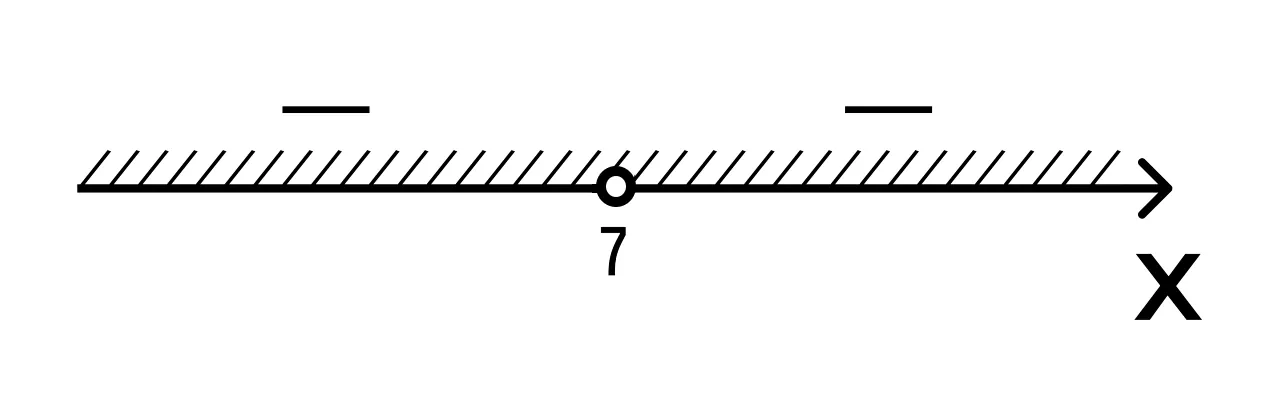
   Очевидно, решениями являются оба промежутка (−∞, 7), (7, +∞).

5.  

Ответ: (−∞, 7), (7, +∞).