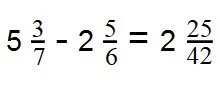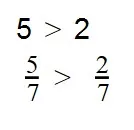Чтобы сравнивать дроби, нужно привести их к общему знаменателю. Далее сравнить числители: дробь с большим числителем будет больше. Если знаменатели одинаковые, то сравниваем числители.
Пример:
- Приводим к 15 —
Сравнение дробей с одинаковыми знаменателями
Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.
Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:
|
Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше. |
А теперь на примерах.
Пример 1. Сравните дроби:
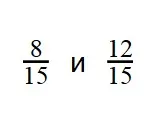
- Мы видим, что знаменатели дробей — равны. Значит сравниваем числители:
8 < 12
12 > 8 - Это значит, что
< 
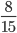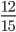Изи!
Пример 2. Сравните дроби:
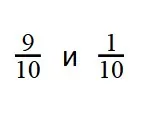
- Как и в прошлом примере, знаменатели дробей — равны. Сравниваем числители:
9 > 10
1 < 10 - Это значит, что
> 
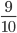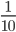
Пример 3. Сравните дроби:
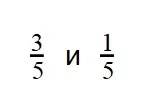
- Знаменатели дробей снова равны. Сравниваем числители:
3 > 1
1 < 3 - Это значит, что
> 
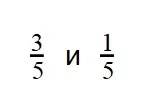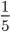
Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший числитель.
Давайте разберем наглядный пример сравнения дробей. Еще больше наглядных примеров — на курсах по математике в онлайн-школе Skysmart!
Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.
- Запишем в виде дробе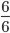й:
и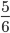 
- А теперь сравним полученные дроби: знаменатели — равны, сравниваем числители:
6 > 5
5 < 6. - Это значит, что >
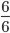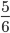
Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.
Сравнение дробей с одинаковыми числителями
Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.
Запомните правило:
|
Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем. |
А теперь наши любимые примеры. Погнали!
Пример 1. Сравните дроби:
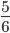
- У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
9 > 7
7 < 9 - Значит, дробь с меньшим знаменателем — больше:
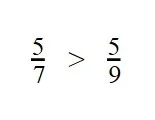
Пример 2. Сравните дроби:
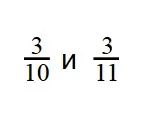
- У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
10 < 11
11 > 10 - Значит дробь с меньшим знаменателем — больше:
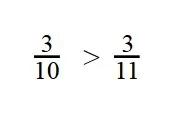
Пример 3. Сравните дроби:
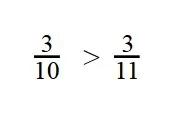
- У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
6 > 3
3 < 6 - Значит, дробь с меньшим знаменателем — больше.
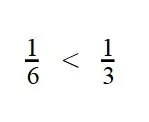
Для наглядности представим ситуацию, в которой вам предстоит разделить торт между тремя друзьями. Это значит, что 6 кусков торта равномерно распределяются по 3 людям: каждому достается 6:3 = 2 по 2 кусочка.
А теперь представим более приятную ситуацию: кусков торта по-прежнему 6, а друзей уже только 2. Тогда каждому достанется по 3 вкуснейших кусочка:
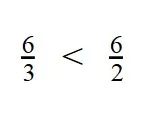
Как видите, сравнение дробей может вам пригодиться в самых неожиданных ситуациях. Теперь, когда снова придется хорошенько задуматься о соотношении кусков торта и приглашенных гостях, изученная тема поможет вам принять верное решение😉.
Получи больше пользы от Skysmart:
-
Прокачивай знания на курсах математики.
-
Выбирай из 1200+ репетиторов по математике.
Записывайся на бесплатные курсы для детей.
Сравнение дробей с разными числителями и разными знаменателями
Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.
Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.
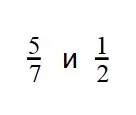
- Нужно подобрать число, которое будет делиться на 7 и на 2, например, 14. Проверим:
14:7 = 2
14 : 2 = 7 - Первую дробь умножаем на дополнительный множитель 2:
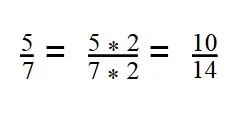
- Вторую дробь умножаем на дополнительный множитель 7:
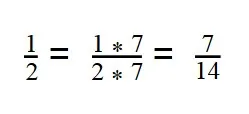
- Дроби приведены к общему знаменателю:
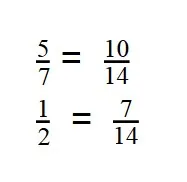
Давайте потренируемся в сравнении дробей.
Пример 1. Сравните дроби:
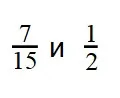
- Приведем дроби к общему знаменателю. 30 делится на 15 и на 2.
30 : 15 = 2
30 : 2 = 15 - Первую дробь умножаем на дополнительный множитель 2:
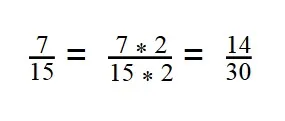
- Вторую дробь умножаем на дополнительный множитель 15:
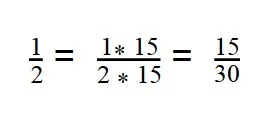
- Дроби приведены к общему знаменателю:
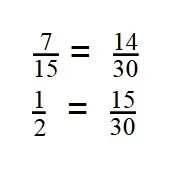
- Если две дроби имеют одинаковые знаменатели, то, согласно правилу, больше та дробь, чей числитель больше:
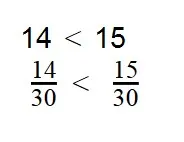
При сравнении неправильных дробей с правильными помните, что неправильная дробь всегда больше правильной.
Пример 2: Сравните дроби:
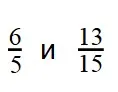
- 6/5 - неправильная дробь.
- Выделим целую часть:
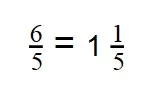
- Значит, что
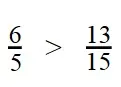
Вычитание смешанных чисел
Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.
- 12 - 7 = 6
12 — уменьшаемое
7 — вычитаемое
5 — разность
В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».
При вычитании дробей действует тот же самый принцип: вычитаемое должно быть меньше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.
Пример 1. Вычислите:
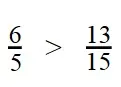
Вычитаемая дробь меньше уменьшаемой
- Выполняем вычитание:
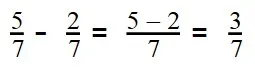
Пример 2.Найдите разность:
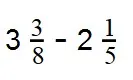
- Смешанные дроби превращаем в неправильные:
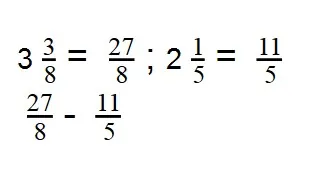
- Чтобы найти разность дробей с разными числителями и знаменателями, нужно привести их к общему знаменателю:
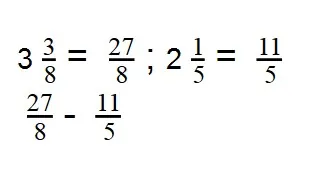
- Наименьшее общее кратное — 40
40 : 8 = 5
40 : 5 = 8 - Умножаем первую дробь на дополнительный множитель 5:
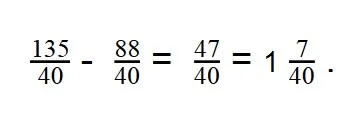
- Умножаем вторую дробь на дополнительный множитель 8:
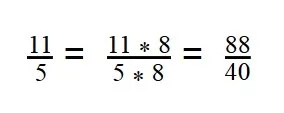
- Дроби приведены к общему знаменателю:
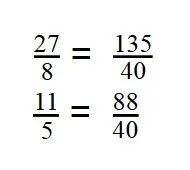
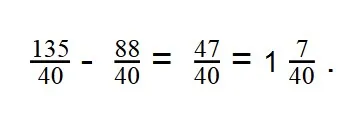
Примеры для самопроверки
Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.
Пример 1. Сравните дроби:
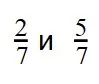
Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что
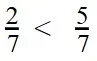
Пример 2. Сравните дроби:
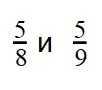
Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что
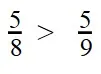
Пример 3. Сравните дроби:
Как решаем:
Ответ:
.
- По правилу сравнения дробей с разными числителями и знаменателями, сначала нужно привести дроби к общему знаменателю:
- Наименьшее общее кратное — 15:
15 : 15 = 1
15 : 5 = 3 - Умножаем первую дробь на дополнительный множитель 1:
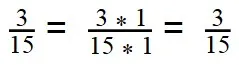
- Умножаем вторую дробь на дополнительный множитель 3:
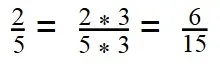
- Дроби приведены к общему знаменателю:
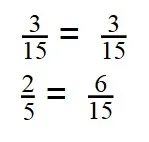
- Сравниваем числители получившихся дробей: 3 < 6
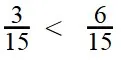
Пример 4. Найдите разность:
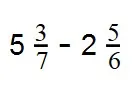
Как решаем:
- Смешанные дроби превращаем в неправильные:
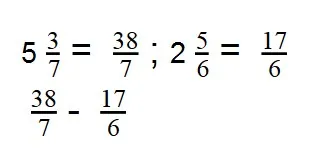
- Чтобы найти разность дробей с разными числителями и знаменателями, нужно привести их к общему знаменателю.
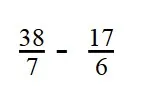
- Наименьшее общее кратное — 42:
42 : 7 = 6
42 : 6 = 7 - Умножаем первую дробь на дополнительный множитель 6:
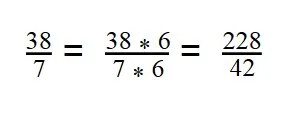
- Умножаем вторую дробь на дополнительный множитель 7:
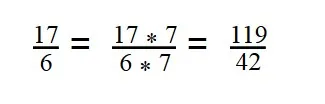
- Дроби приведены к общему знаменателю.
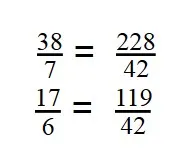
- Теперь можно вычитать:
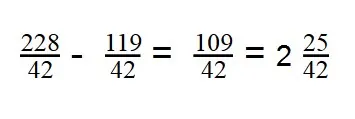
Ответ:
