Тригонометрическая окружность - это окружность радиуса 1 на координатной плоскости с центром в начале координат. На ней углы измеряются по часовой стрелке от положительной полуоси OX. Используется для определения тригонометрических функций углов.
Пример:
- sin(0) = 0
- cos(π/2) = 0
- tan(π) = 0
Единичная окружность в тригонометрии
При изучении тригонометрии используют единичную окружность. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
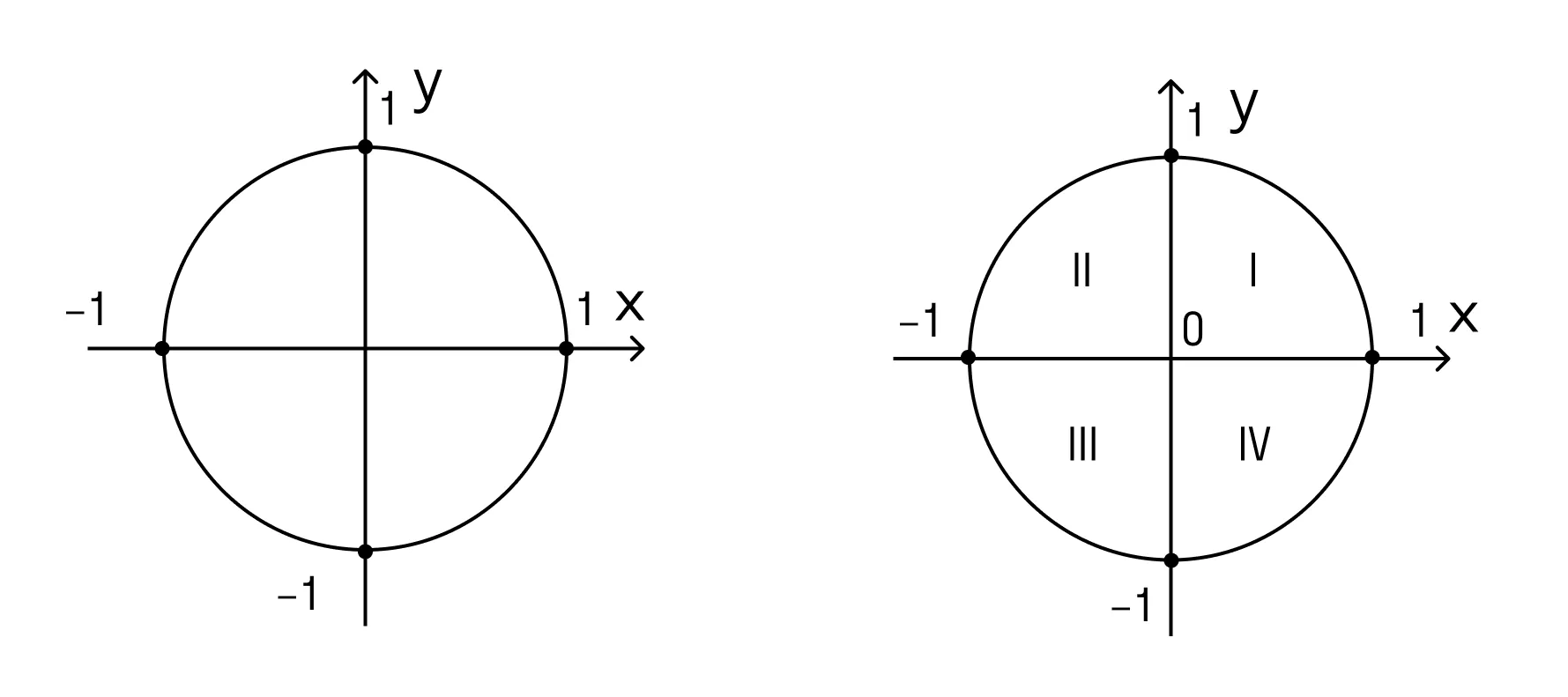
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол принято считать против часовой стрелки между положительным направлением оси OX и лучом OA.
Величины углов не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании.
Все углы, которые принадлежат одной четверти, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
Если угол находится в первой четверти, все тригонометрические функции имеют положительные значения.
Для угла во второй четверти синус положителен, косинус, тангенс и котангенс — отрицательны.
В третьей четверти синус и косинус отрицательны, а тангенс и котангенс — положительны.
В четвертой четверти синус отрицателен, косинус положителен, тангенс и котангенс — отрицательны.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
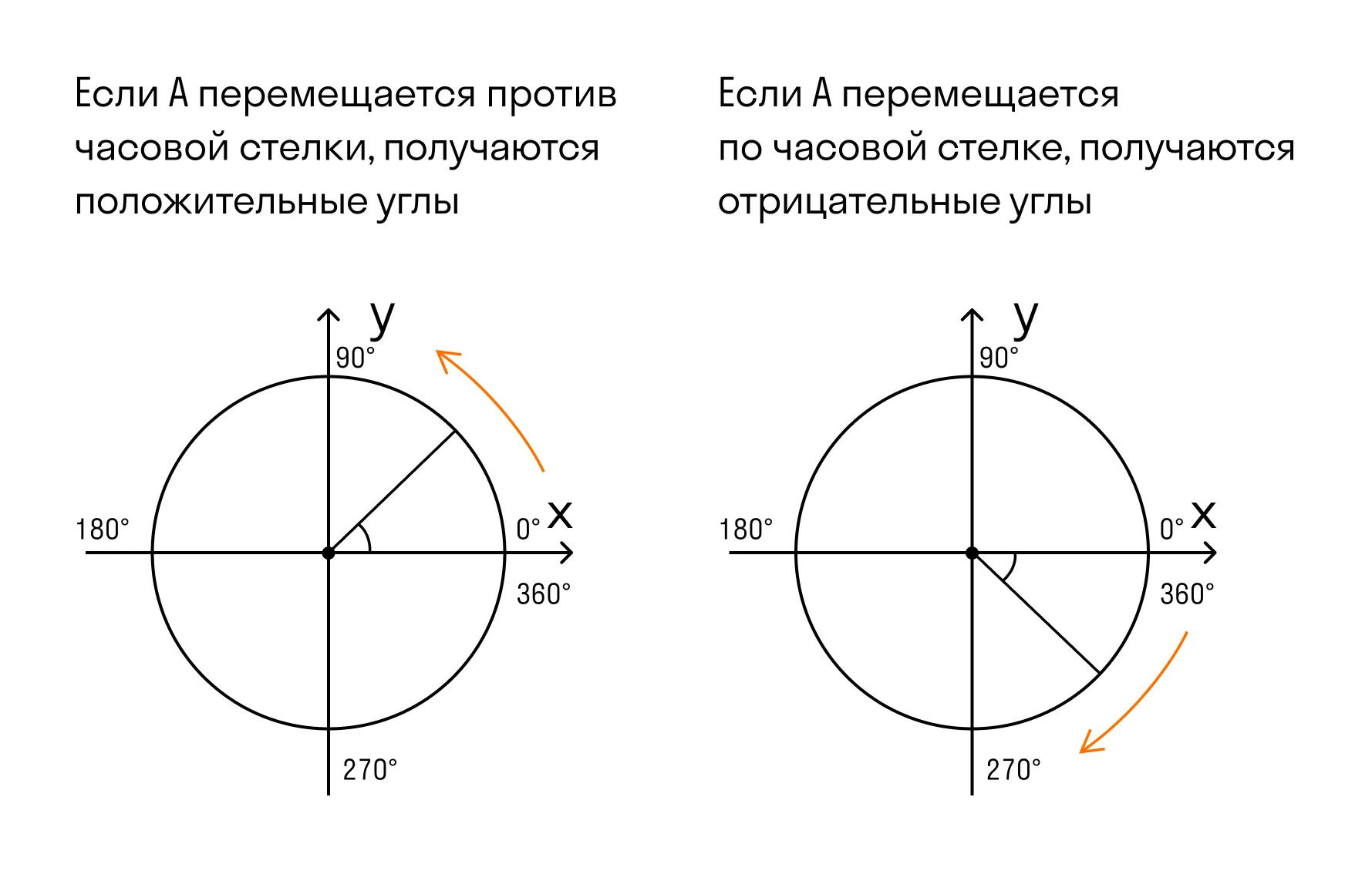
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
2π радиан = 360°
1 радиан = (360/2π) градусов = (180/π) градусов
360° = 2π радиан
1° = (2π/360) радиан = (π/180) радиан
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Для чего можно использовать единичную окружность
определить синус, косинус, тангенс и котангенс угла
найти значения тригонометрических функций для некоторых значений числового и углового аргумента
вывести основные формулы тригонометрии
применить формулы приведения
найти области определения и области значений тригонометрических функций
определить периодичность тригонометрических функций
определить четность и нечетность тригонометрических функций
определить промежутки возрастания и убывания тригонометрических функций
определить промежутки знакопостоянства тригонометрических функций
применить радианное измерение углов
найти значения обратных тригонометрических функций
решить простейшие тригонометрические уравнения
решить простейшие тригонометрические неравенства.
