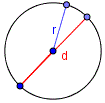
Геометрическая фигура (лат. figura — внешний вид, образ) (англ. geometric figure) — геометрический термин, формально применимый к множеству точек, линий или поверхностей.
Примеры:
Изучая основные геометрические фигуры, важно уметь правильно их обозначать. Например, знание
- треугольник
- квадрат
- круг
- сфера
- куб
Для кого эта статья:
- Студенты и школьники, изучающие геометрию
- Преподаватели математики и курсов по математике
- Все желающие узнать о геометрических фигурах и их свойствах
Основные понятия
Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.
Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.
Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.

Обучение на курсах по математике поможет быстрее разобраться в видах и свойствах геометрических фигур.
Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.
Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.
Периметром принято называть сумму длин всех сторон многоугольника. Периметр обозначается заглавной латинской P.
Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм2);
- квадратный сантиметр (см2);
- квадратный дециметр (дм2);
- квадратный метр (м2);
- квадратный километр (км2);
- гектар (га).
Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.
Если все точки фигуры принадлежат одной плоскости, значит она является плоской.
Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.
Примеры объемных геометрических фигур:
- шар,
- конус,
- параллелепипед,
- цилиндр,
- пирамида,
- сфера.
Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.
Прямоугольник
Прямоугольник — параллелограмм, у которого все углы прямые.
Свойства прямоугольника:
- Диагонали прямоугольника равны и делятся в точке пересечения пополам.
- Около прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.
Узнать площадь прямоугольника помогут следующие формулы:
- S = a × b, где a, b — ширина и высота прямоугольника.

- S = a × √(d2 - а2), где а — известная сторона, d — диагональ.
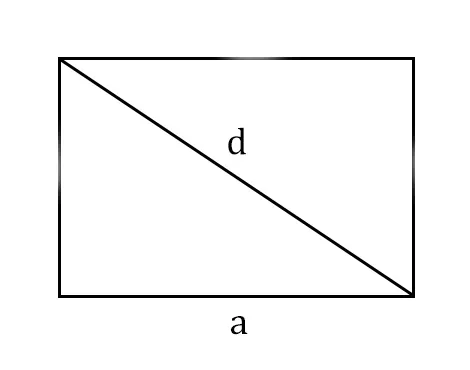
Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.
- S = 0,5 × d2 × 𝑠𝑖𝑛(𝑎), где d — диагональ.
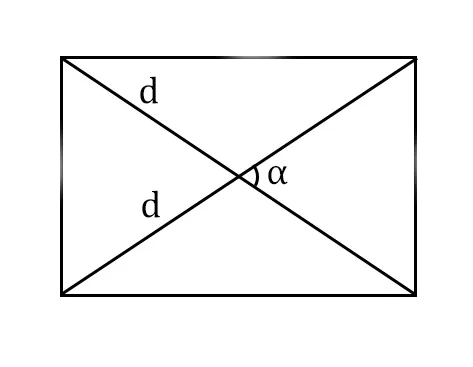
Периметр прямоугольника — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.

Получи больше пользы от Skysmart:
-
Прокачивай знания на курсах математики
-
Выбирай из 1200+ репетиторов по математике
Записывайся на бесплатные курсы для детей
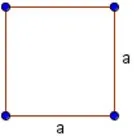
Квадрат
Квадрат — это тот же прямоугольник, у которого все стороны равны.
Свойства квадрата:
- Все стороны равны.
- Все углы равны и составляют 90 градусов.
- Диагонали квадрата равны и перпендикулярны.
- У квадрата центры вписанной и описанной окружности совпадают и находятся в точке пересечения его диагоналей.
Найти площадь квадрата легко:
- S = а2, где a — сторона квадрата.
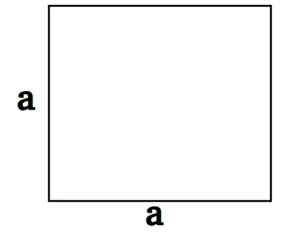
- S = d2 : 2, где d — диагональ.
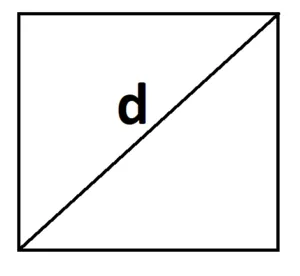
Периметр квадрата — это длина стороны, умноженная на четыре.
P = 4 × a, где a — длина стороны.
Трапеция
Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.
Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.
Как найти площадь трапеции:
S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.
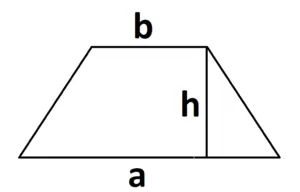
Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.
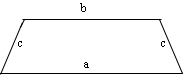
Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.
P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.
Параллелограмм и ромб
Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны
Ромб — это параллелограмм с равными сторонами.
Свойства параллелограмма:
- Противоположные стороны и углы равны.
- Сумма любых двух соседних углов равна 180 градусам.
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Каждая диагональ делит фигуру на два равных треугольника.
Общие формулы расчета площади фигур:
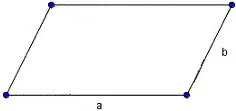
- S = a × h, где a — сторона, h — высота.
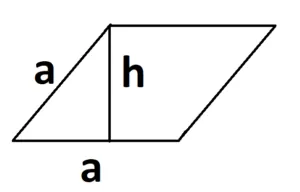
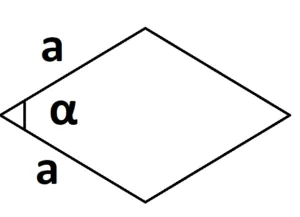
- S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. В случае с ромбом стороны равны, поэтому формула примет вид S = a × a × sinα или S = a2 × sinα.
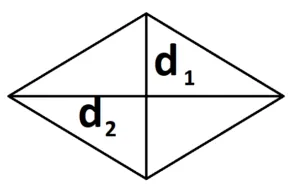
- Для ромба: S = 0,5 × (d1 × d2), где d1,d2 — две диагонали. Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.
Периметр ромба — это произведение длины стороны на четыре.
P = 4 × a, где a — длина стороны.
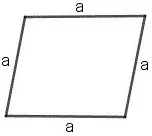
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Треугольник
Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.
Виды треугольников:
- Прямоугольный. Один угол прямой, два других менее 90 градусов.
- Остроугольный. Градус угла больше 0, но меньше 90 градусов.
- Тупоугольный. Один угол тупой, два других острые.
Свойства треугольника:
- В треугольнике против большего угла лежит большая сторона — и наоборот.
- Сумма углов треугольника равна 180 градусов.
- Все углы равностороннего треугольника равны 60 градусам.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.
- Если известна сторона и высота.
S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.
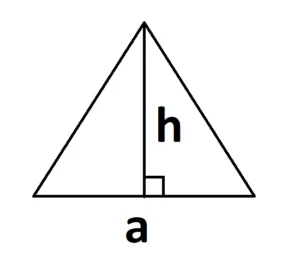
Основание может быть расположено иначе, например так:
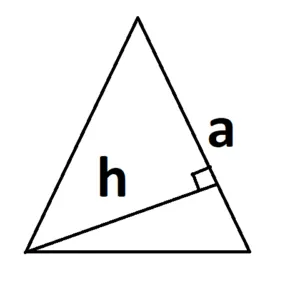
При тупом угле высоту можно отразить на продолжение основания:
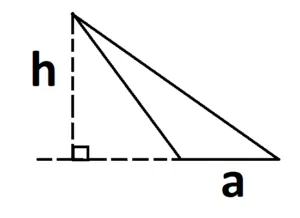
При прямом угле основанием и высотой будут его катеты:

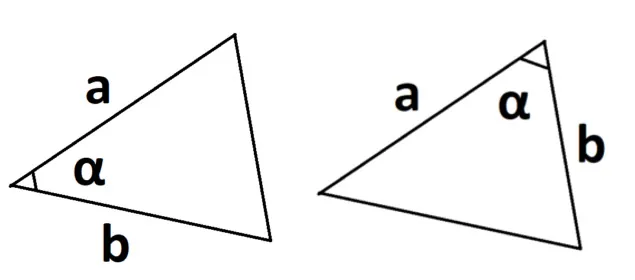
- Если известны две стороны и синус угла.
S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.
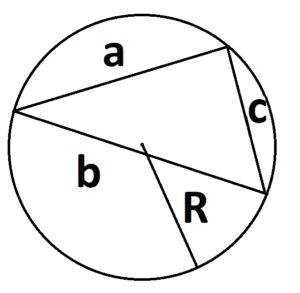
- Если есть радиус описанной окружности.
S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.
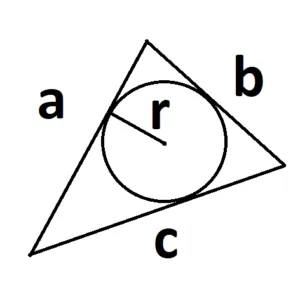
- Если есть радиус вписанной окружности.
S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.
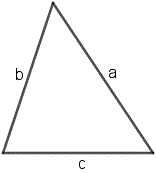
Периметр треугольника — это сумма длин трех его сторон.
P = a + b + c, где a, b, c — длина стороны.
Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.
P = 3 × a, где a — длина стороны.
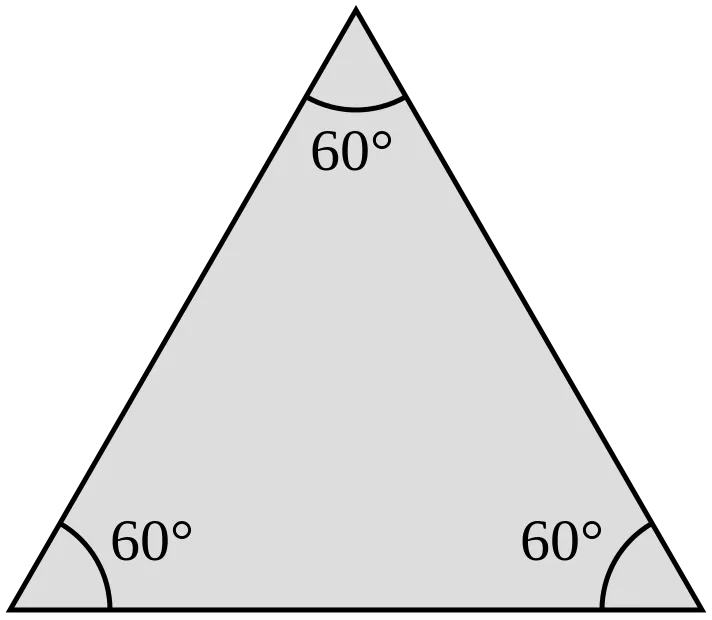
Круг
Круг — это это часть плоскости, которая лежит внутри окружности.
Окружность — это граница круга.
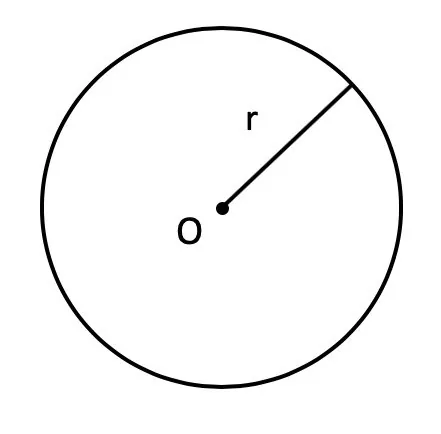
Радиус окружности — это расстояние от центра окружности до любой точки на ней.
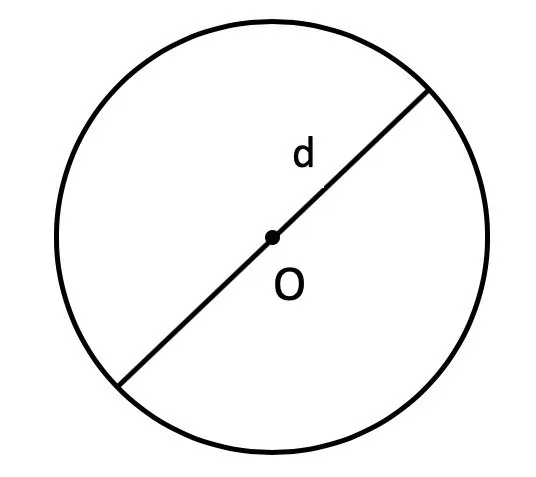
Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.
Формулы площади круга:
- S = π × r2, где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
- S = π × d2 : 4, где d — это диаметр.
- S = L2 : (4 × π), где L — это длина окружности.

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.
L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.