Разложение многочлена способом группировки

Основные понятия

Мы знаем, что слово «множитель» происходит от слова «умножать».

Возьмем, например, число 12. Чтобы разложить его на множители, нужно написать его по-другому, а именно в виде «произведения» множителей. 

Число 12 можно получить, если умножить 2 на 6. А 6 можно представить, как произведение 2 и 3. Вот так:

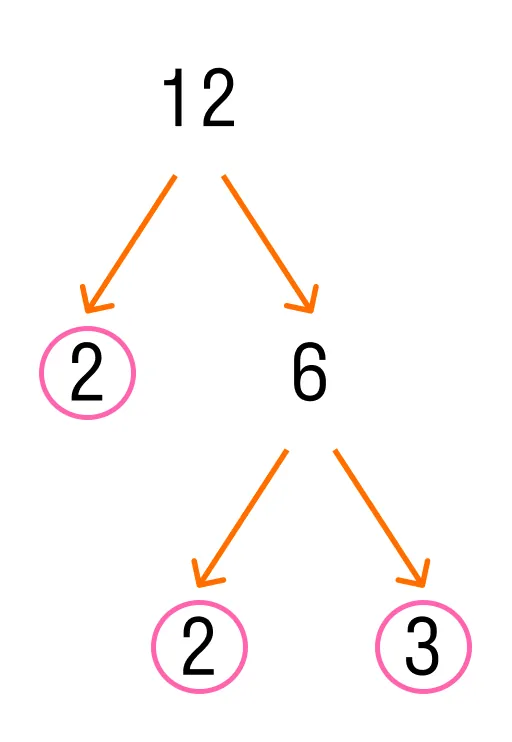
Так выглядит пошаговое разложение на множители. Числа, которые обведены в кружок на картинке — это множители, которые дальше разложить уже нельзя. 

Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.

5 способов разложения многочлена на множители

 

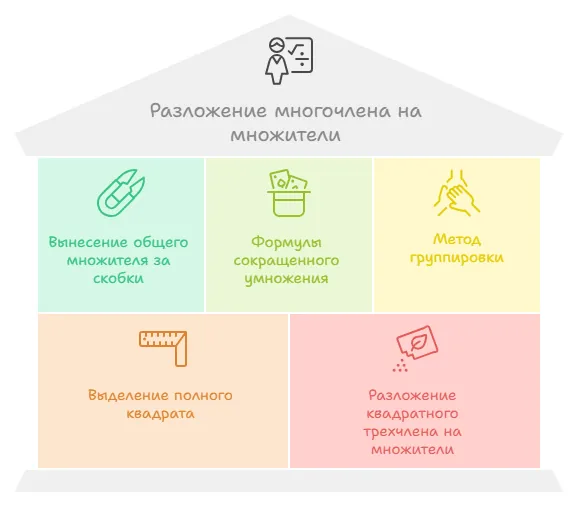
1. Вынесение общего множителя за скобки.


2. Формулы сокращенного умножения.


3. Метод группировки.


4. Выделение полного квадрата.


5. Разложение квадратного трехчлена на множители.

107K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Прокачивай знания на курсах математики.

• Выбирай из 1200+ репетиторов по математике.

• Записывайся на бесплатные курсы для детей.

Способ группировки множителей

Разложение на множители методом группировки возможно, когда многочлены не имеют общего множителя для всех членов многочлена. 

Этот способ применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку. И тогда исходный многочлен будет представлен в виде произведения, что значительно облегчает задачу.

Разложить на множители методом группировки можно в три этапа:

 

1. Объединить слагаемые многочлена в группы, которые содержат общий множитель. Для наглядности их можно подчеркнуть.


2. Вынести общий множитель за скобки.


3. Полученные произведения имеют общий множитель в виде многочлена, который нужно вынести за скобки.

Объединить члены многочлена в группы можно по-разному. И не всегда группировка может быть удачной для последующего разложения на множители. В таком случае нужно продолжить эксперимент и попробовать объединить в группы другие члены многочлена.

Чтобы понять эти сложные выражения, применим правило группировки множителей при решении примеров. Рассмотрим два способа.

Пример 1. Разложить на множители методом группировки: up - bp + ud - bd.

Как решаем:

1 способ	2 способ
up - bp + ud - bd = (up - bp) + (ud - bd) Заметим, что в первой группе повторяется p, а во второй — d. Вынесем в первой группе общий множитель p, а во второй общий множитель d. Получим: p(u - b) + d(u - b). Заметим, что общий множитель (u - b). Вынесем его за скобки:  (u - b)(p + d).  Группировка множителей выполнена.	up - bp + ud - bd = (up + ud) - (bp + bd) Заметим, что в первой группе повторяется u, а во второй — b. Вынесем в первой группе общий множитель u, а во второй общий множитель b. Получим: u(p + d) - b(p + d). Заметим, что общий множитель (p + d). Вынесем его за скобки:  (p + d) (u - b). Группировка множителей выполнена.

От перестановки мест множителей произведение не меняется, поэтому оба ответа верны:

(u - b)(p + d) = (p + d)(u - b).

Вот так работает алгоритм разложения многочлена на множители способом группировки. Продолжим практиковаться на примерах.

Пример 2. Разложить на множители выражение: c(m - n) + d(m - n).

Как решаем:

 

1. Найдем общий множитель: (m - n)


2. Вынесем общий множитель за скобки: (m - n)(c + d). 

Ответ: c(m - n) + d(m - n) = (m - n)(c + d).

Пример 3. Разложить на множители  с помощью группировки: 5x - 12z (x - y) - 5y.

Как решаем: 

5x - 12z (x - y) - 5y = 5x - 5y - 12z (x - y) = 5(x - y) - 12z (x - y) = (x - y) (5 - 12z)

Ответ: 5x - 12z (x - y) - 5y = (x - y) (5 - 12z).

Иногда для вынесения общего многочлена нужно заменить все знаки одночленов в скобках на противоположные. Для этого за скобки выносится знак минус, а в скобках у всех одночленов меняем знаки на противоположные.

Проверим как это на следующем примере.

Пример 4. Произвести разложение многочлена на множители способом группировки: ax² - bx² + bx - ax + a - b.

Как решаем:

 

1. Сгруппируем слагаемые по два и вынесем в каждой паре общий множитель за скобку:

ax² - bx² + bx - ax + a - b = (ax² - bx²) + (bx - ax) + (a - b) = x²(a - b) - x(a - b) + (a - b)

Получили три слагаемых, в каждом из которых есть общий множитель (a - b).

1. Теперь вынесем за скобку (a - b), используя распределительный закон умножения:

x²(a - b) + x(b - a) + (a - b) = (a - b)(x² + x + 1)

Ответ: ax² - bx² + bx - ax + a - b = (a - b)(x² + x + 1)

Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.