Особенности задания
Задание №6 предназначено для анализа физического явления через основные положения, законы и формулы. В нём представлена определённая ситуация, где две физические величины вынуждены изменяться, а вам предстоит определить, каким образом.
Например:
Тело свободно падает с высоты h. Как при этом меняются его кинетическая и потенциальная энергии?
Для каждой величины определите соответствующий характер её изменения.
- Увеличивается.
- Уменьшается.
- Не изменяется.
|
Кинетическая энергия |
Потенциальная энергия |
|---|---|
|
2 |
1 |
Ответ: 21
Задание оценивается максимально 2 баллами, если вам удалось верно определить изменение двух величин, 1 баллом — если удалось верно определить изменение только одной величины, 0 баллами — если оба изменения вы указали неверно.
Советы по решению
- Для начала определите, о каком физическом процессе идёт речь (механика, электродинамика и т. д.).
- Выявите главные величины, которые нужно сравнивать (скорость, сила, энергия и т. д.).
- Всегда опирайтесь на законы сохранения (энергии, импульса) и фундаментальные уравнения (например, второй закон Ньютона).
- Размышляйте о том, как изменение одной величины влияет на другие. Например, увеличение массы ведёт к уменьшению ускорения при той же силе.
- Научитесь читать и анализировать графики изменения физических величин.
- Решайте много практических примеров, чтобы автоматизировать подход к анализу.
Предлагаем воспользоваться последним советом и попрактиковаться в решении задач.
Получи больше пользы от Skysmart:
-
Подтяни оценки на курсах по физике.
-
Выбирай из 890+ репетиторов по физике.
Записывайся на бесплатные курсы для детей.
Разбор заданий
Задача 1
На поверхности воды плавает сплошной пробковый брусок. Как изменятся глубина погружения бруска и сила Архимеда, действующая на брусок, если его заменить сплошным бруском той же плотности и высоты, но большей массы?
Для каждой величины определите соответствующий характер изменения.
- Увеличится.
- Уменьшится.
- Не изменится.
|
Глубина погружения |
Сила Архимеда |
|---|---|
Решение:
Для начала вспомним формулу для нахождения силы Архимеда:
Fарх = ρжидк ⋅ g ⋅ Vп.т., где
ρжидк — плотность жидкости, в которую погружено тело,
g ≈ 9,8 м/с2 — ускорение свободного падения,
Vп.т. — объём погружённой части тела.
Исходя из того, что тело плавает (не всплывает и не погружается на дно), можно сделать вывод: сила Архимеда в данной задаче уравновешивается силой тяжести: Fарх = Fтяж = mg
- Если масса тела возрастёт, то возрастёт и сила тяжести. А раз она уравновешивается силой Архимеда, то и Fарх станет больше.
- Помимо этого, подобный же вывод можно сделать из следующей мысли: если масса тела возрастёт при той же плотности, то объём тела тоже должен стать больше. Это повлечёт за собой и увеличение объёма погружённой части тела, от которого зависит выталкивающая сила.
Итого:
Для того чтобы определить характер изменения глубины погружения, выразим её из формул путём преобразований.
|
Fарх=Fтяж |
Сила Архимеда уравновешивается силой тяжести |
|
mтелаg = ρжидк ⋅ g ⋅ Vп.т. |
Распишем обе стороны |
|
mтела = ρжидк ⋅ Vп.т. |
Сократим на величину g |
|
Vтела ⋅ ρтела = ρжидк ⋅ Vп.т. |
Раскроем массу тела |
|
ρтела ⋅ Sосн ⋅ hтела = ρжидк ⋅ Sосн ⋅ hп.т. |
Вспомним, что объём равен произведению площади основания на высоту |
|
|
Сократим на площадь основания и выразим глубину погружения |
В задаче сказано, что плотность и высота тела не менялись, значит,
Ответ: 31
Задача 2
Теннисный мяч бросают под углом к горизонту с горизонтальной площадки. Затем его бросают во второй раз с той же площадки, сохранив неизменным модуль начальной скорости, но увеличив угол между вектором начальной скорости и площадкой. Как изменяются во втором случае по сравнению с первым высота подъёма мяча и его кинетическая энергия в наивысшей точке траектории?
Для каждой величины определите соответствующий характер ее изменения.
- Увеличивается.
- Уменьшается.
- Не изменяется.
|
Высота подъёма |
Кинетическая энергия |
|---|---|
Решение:
Представим описанный процесс в виде графика и вспомним соответствующие формулы.
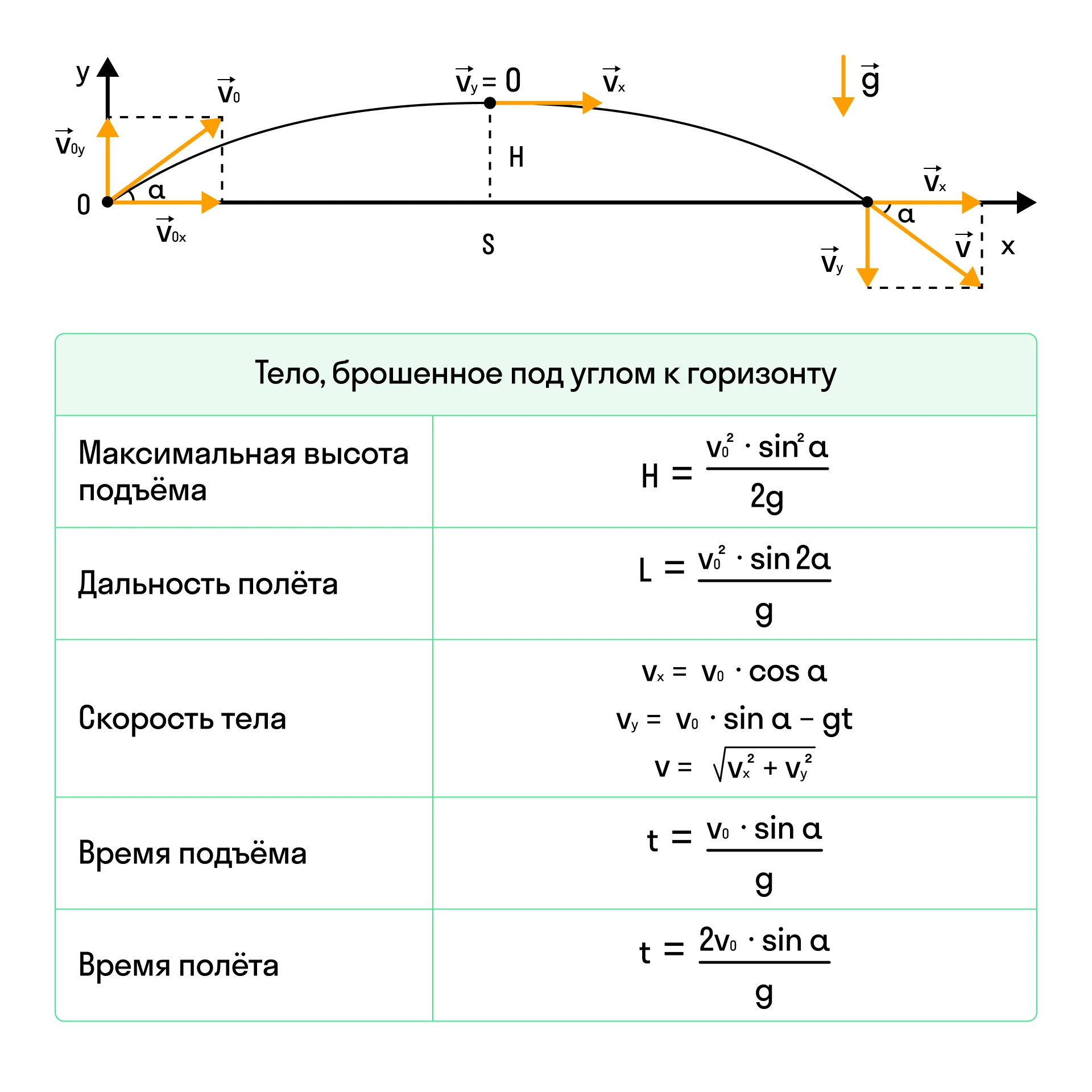
Высота подъёма описывается формулой
При этом начальная скорость броска по условию задачи не меняется, а значит,
при увеличении угла броска высота подъёма увеличится .
Кинетическая энергия выражается формулой
Для углов от 0 до 180° верно утверждение: «чем больше угол, тем меньше косинус угла». Значит,
при увеличении угла броска кинетическая энергия в верхней точке уменьшится .
Ответ: 21
Задача 3
Искусственный спутник вращается вокруг Земли, при этом высота его полёта уменьшилась с 500 км до 100 км. Как изменились в результате этого перехода частота обращения спутника вокруг Земли и его линейная скорость на орбите?
Для каждой величины определить соответствующий характер изменения.
- Увеличилась.
- Уменьшилась.
- Не изменилась.
|
Частота |
Линейная скорость |
|---|---|
Решение:
Задача относится к теме «Движение по окружности», а также задействует закон всемирного тяготения.
Центростремительное движение спутника обеспечивается гравитацией, а значит, центростремительную силу можно рассчитать как:
М — масса планеты,
m — масса спутника, R — радиус орбиты.
Центростремительное ускорение равно
По второму закону Ньютона
Так как гравитационная постоянная — это константа, а масса планеты в задаче не менялась, линейная скорость будет зависеть от радиуса орбиты, причём обратно пропорционально: чем меньше радиус, тем линейная скорость больше.
Следовательно,
Частоту можно рассчитать по формуле
Подставим в формулу линейную скорость
Таким образом, при уменьшении радиуса орбиты
Ответ: 11
Мы разобрали лишь небольшую часть возможных заданий. На реальном экзамене вам могут встретиться задачи на закон Гука, колебания математического и пружинного маятников, изменение силы трения и другие увлекательные темы. Чтобы быть на 100% готовыми ко всем возможным вариантам заданий, приходите на курс подготовки к ЕГЭ по физике в онлайн-школу Skysmart. Мы поможем вам уверенно разобраться в самых сложных темах и достичь отличного результата!
