Закон cохранения импульса

Импульс: что это такое

Как-то раз Рене Декарт (это который придумал ту самую декартову систему координат) решил, что каждый раз считать силу, чтобы описать процессы — как-то лень и сложно.

Для этого нужно ускорение, а оно не всегда очевидно. Тогда он придумал такую величину, как импульс. Импульс можно охарактеризовать, как количество движения — это произведение массы на скорость.

Импульс тела p — импульс тела [кг · м/с] m — масса тела [кг] v — скорость [м/с]

Закон сохранения импульса

В физике и правда ничего не исчезает и не появляется из ниоткуда. Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:

Закон сохранения импульса Векторная сумма импульсов тел в замкнутой системе постоянна

А выглядит — вот так:

Закон сохранения импульса pn — импульс тела [кг · м/с]

Простая задачка

Мальчик массой m = 45 кг плыл на лодке массой M = 270 кг в озере и решил искупаться. Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?

Решение:

Запишем закон сохранения импульса для данного процесса.

— это импульс системы мальчик + лодка до того, как мальчик спрыгнул,

— это импульс мальчика после прыжка,

— это импульс лодки после прыжка.

Изобразим на рисунке, что происходило до и после прыжка.

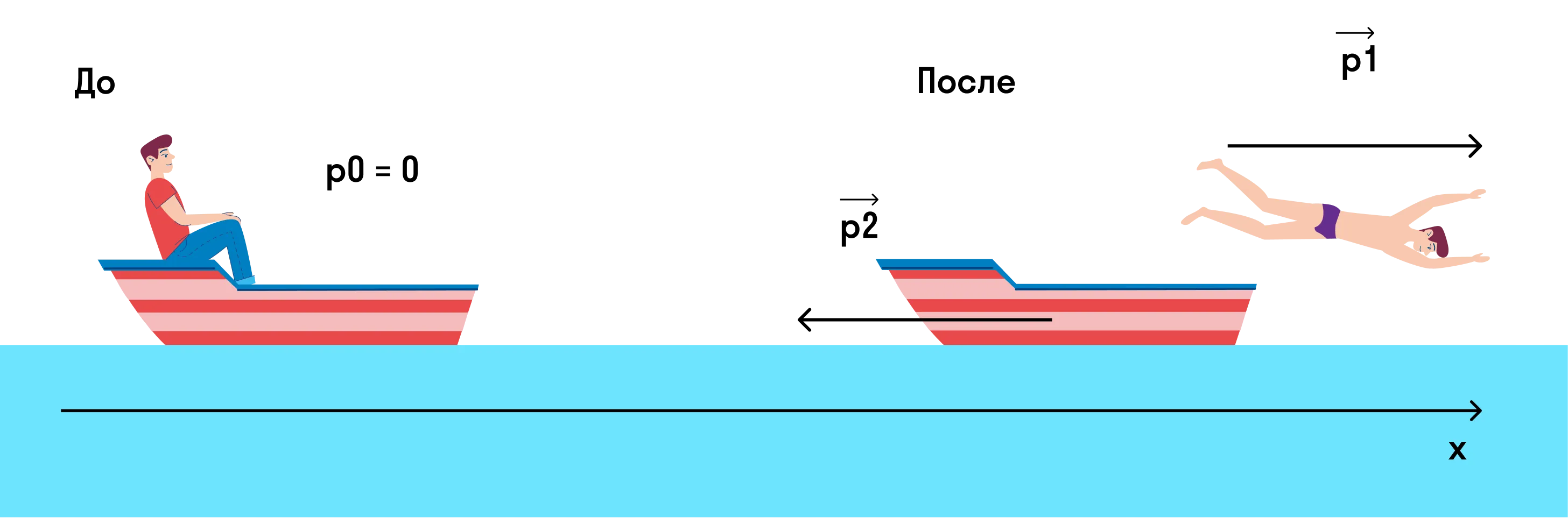
Если мы спроецируем импульсы на ось х, то закон сохранения импульса примет вид

Подставим формулу импульса.
, где:
— масса мальчика [кг]
— скорость мальчика после прыжка [м/с]
— масса лодки [кг]
— скорость лодки после прыжка [м/с]

Выразим скорость лодки :

Подставим значения:
м/с

Ответ: скорость лодки после прыжка равна 0,5 м/с

👉 Посмотри возможности нашей онлайн школы Skysmart!
Будешь щёлкать задачки как орешки!

Задачка посложнее

Тело массы m₁ = 800 г движется со скоростью v₁ = 3 м/с по гладкой горизонтальной поверхности. Навстречу ему движется тело массы m₂ = 200 г со скоростью v₂ = 13 м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.

Решение: Для данной системы выполняется закон сохранения импульса:

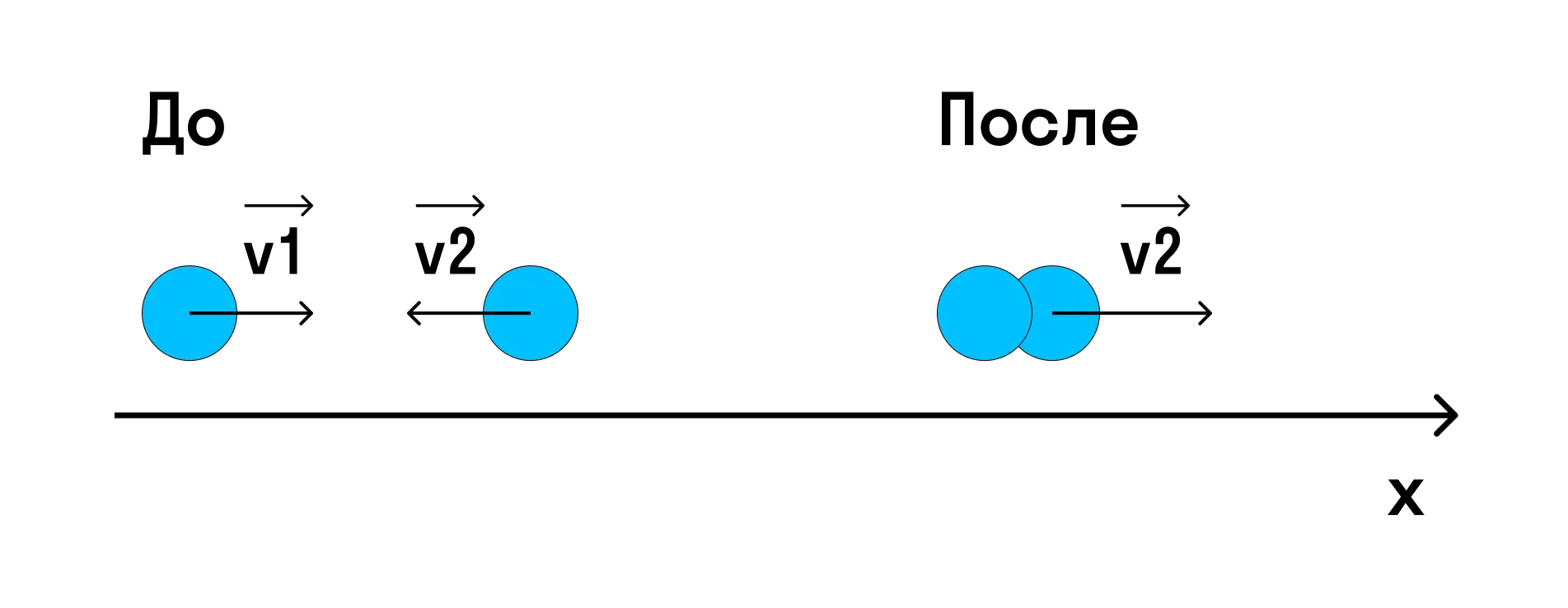
Импульс системы до удара — это сумма импульсов тел, а после удара — импульс «получившегося» в результате удара тела.

Спроецируем импульсы на ось х:

После неупругого удара получилось одно тело массы , которое движется с искомой скоростью:

Отсюда находим скорость тела, образовавшегося после удара:

Переводим массу в килограммы и подставляем значения:

м/с

В результате мы получили отрицательное значение скорости. Это значит, что в самом начале на рисунке мы направили скорость после удара неправильно.

Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси X. Это никак не влияет на получившееся значение.

Ответ: скорость системы тел после соударения равна v = 0,2 м/с.

170.4K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подтяни оценки на курсах по физике.

• Выбирай из 890+ репетиторов по физике.

• Записывайся на бесплатные курсы для детей.

Второй закон Ньютона в импульсной форме

Второй закон Ньютона в импульсной форме можно получить следующим образом. Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.

Запишем второй закон Ньютона, спроецированный на ось х, сонаправленную с направлением движения и ускорением:

Применим выражение для ускорения

В этих уравнениях слева находится величина a. Так как левые части уравнений равны, можно приравнять правые их части

Полученное выражение является пропорцией. Применив основное свойство пропорции, получим такое выражение:

В правой части находится — это разница между конечной и начальной скоростью.

Преобразуем правую часть

Раскрыв скобки, получим

Заменим произведение массы и скорости на импульс:

Подставляем:

Или, сокращенно:

То есть, вектор – это вектор изменения импульса .

Тогда второй закон Ньютона в импульсной форме запишем так

Вернемся к векторной форме, чтобы данное выражение было справедливо для любого направления вектора ускорения.

Задачка про белку отлично описывает смысл второго закона Ньютона в импульсной форме Белка с полными лапками орехов сидит на гладком горизонтальном столе. И вот кто-то бесцеремонно толкает ее к краю стола. Белка понимает законы Ньютона и предотвращает падение. Но как?

Решение:

Чтобы к белке приложить силу, которая будет толкать белку в обратном направлении от края стола, нужно создать соответствующий импульс (вот и второй закон Ньютона в импульсной форме подъехал).

Ну, а чтобы создать импульс, белка может выкинуть орехи в сторону направления движения — тогда по закону сохранения импульса ее собственный импульс будет направлен против направления скорости орехов.

Реактивное движение

В основе движения ракет, салютов и некоторых живых существ: кальмаров, осьминогов, каракатиц и медуз — лежит закон сохранения импульса. В этих случаях движение тела возникает из-за отделения какой-либо его части. Такое движение называется реактивным.

Яркий пример реактивного движения в технике — движение ракеты, когда из нее истекает струя горючего газа, которая образуется при сгорании топлива.

Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:

Сила называется реактивной. Это та сила, которая возникает в процессе отделения части тела. Особенностью реактивной силы является то, что она возникает без взаимодействия с внешними телами.

Закон сохранения импульса позволяет оценить скорость ракеты.

m_г · v_г = m_р · v_р,
где m_г — это масса горючего,

v_г — скорость горючего,

m_р — масса ракеты,

v_р — скорость ракеты.

Отсюда можно выразить скорость ракеты:

v_р = m_г · v_г / m_р

Скорость ракеты при реактивном движении vр = mг · vг / mр mг — это масса горючего [кг] vг — скорость горючего [м/с] mр — масса ракеты [кг] vр — скорость ракеты [м/с]

Эта формула справедлива для случая мгновенного сгорания топлива. Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!