Момент силы – это векторная величина, характеризующая вращательное действие силы относительно точки или оси. Момент силы M рассчитывается как произведение силы F на плечо силы l:
Примеры:
- Если F = 10 Н и l = 2 м, то M = 20 Н·м.
- Когда F = 5 Н и l = 0,5 м, то M = 2,5 Н·м.
Для кого эта статья:
- Читатели, интересующиеся темой статьи
- Специалисты в данной области знаний
- Студенты или школьники, стремящиеся углубить свои знания
Плечо силы
Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.
Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.
Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.

То есть перпендикуляр, проведенный от точки опоры до линии, вдоль которой действует сила — это плечо силы.
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!

Рычаг
В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.
Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.

Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.
Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.

|
Правило равновесия рычага Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил. F1, F2 — силы, действующие на рычаг l1, l2 — плечи этих сил |
Получи больше пользы от Skysmart:
-
Подготовься к ОГЭ на пятёрку
-
Подготовься к ЕГЭ на высокие баллы
Записывайся на бесплатные курсы для детей
Решай задания в бесплатном тренажёре ЕГЭ
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
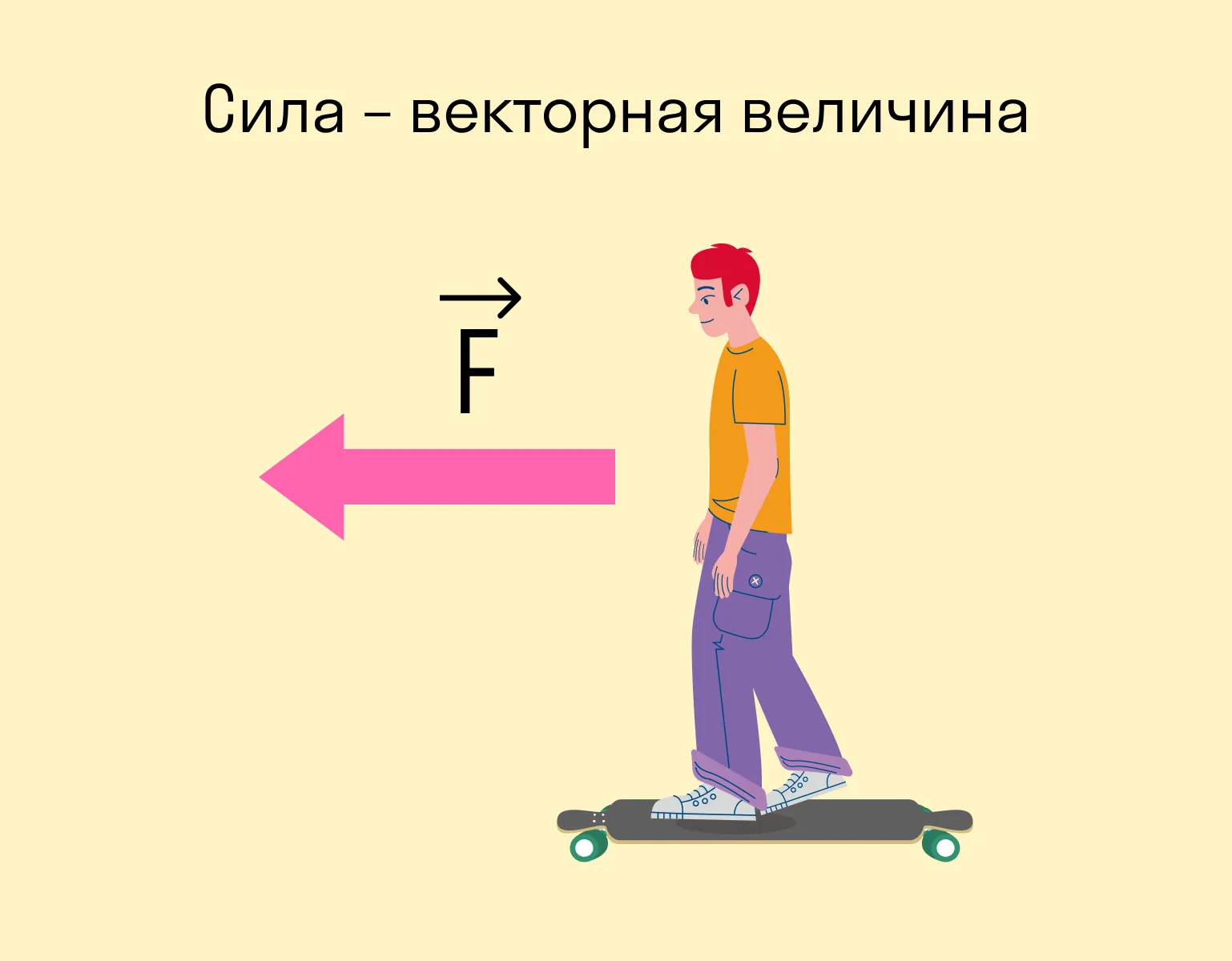
- Сила — это физическая векторная величина, является мерой действия тела на другое тело.
Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Момент силы
Момент силы единица измерения — это ньютон-метр (Н⋅м или N⋅m) в Международной системе единиц (СИ).
- Пример: если сила в 10 ньютонов действует на рычаг длиной 0,5 метра, момент силы будет
При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.
Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.
Момент силы — это произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.
|
Момент силы M = Fl M — момент силы [Н*м] |
Для примера представьте, что вы забыли, как открывать двери. Стоите перед дверью и раздумываете, как легче это сделать.
Для начала приложим силу к краю двери — туда, где самый длинный рычаг. Открылась!
А что если толкнуть дверь ближе к креплению — там, где плечо намного короче? Для этого придется приложить силу большего значения.
Вывод: чтобы повернуть дверь, нужен крутящий момент определенного значения. Чем больше плечо силы, тем меньше значение силы, которую нужно приложить — и наоборот. Поэтому нам легче толкать дверь там, где плечо силы больше.

Похожая история с гаечным ключом. Чтобы закрутить гайку, нужно взяться за ручку подальше от гайки. За счет увеличения плеча мы уменьшаем значение силы, которую нужно приложить.
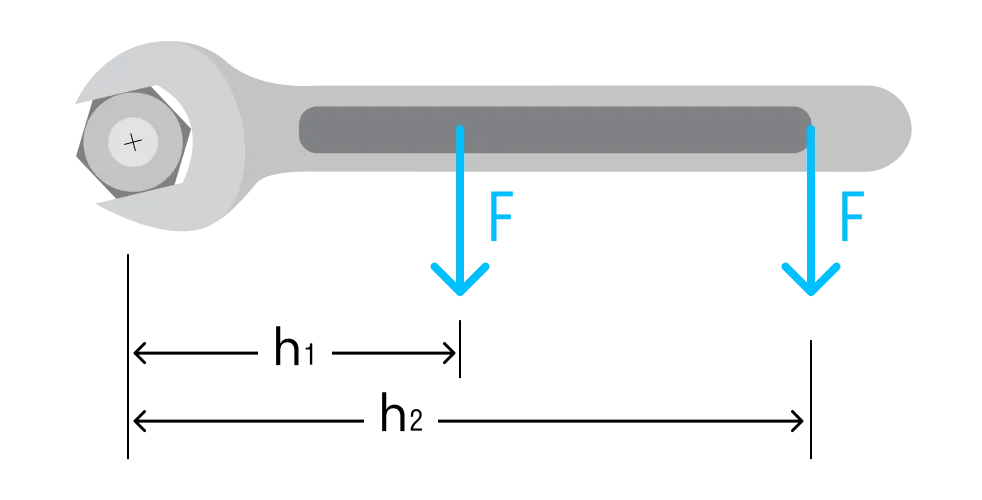
Расчет момента силы
Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.
Расстояние между точками A и B — 3 метра.
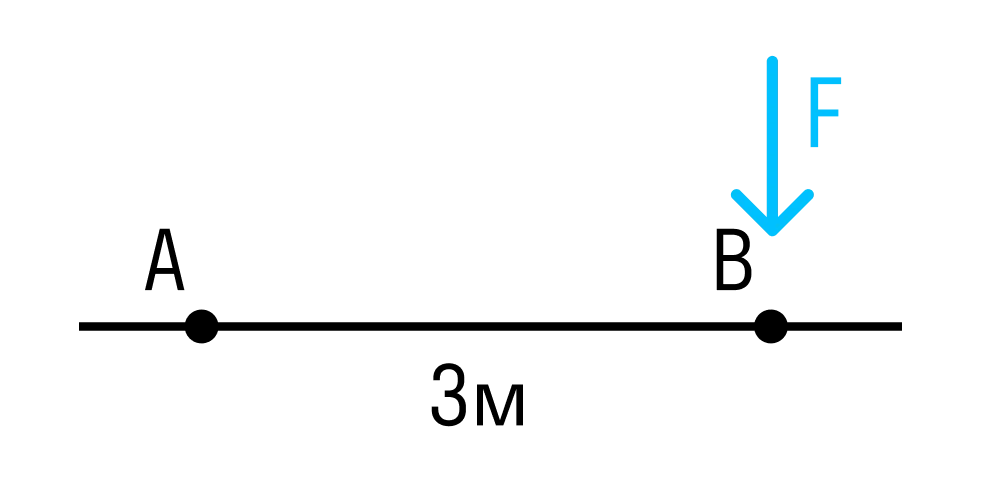
Момент силы относительно точки A:
МА=F×AB=F×3м
Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.
Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!
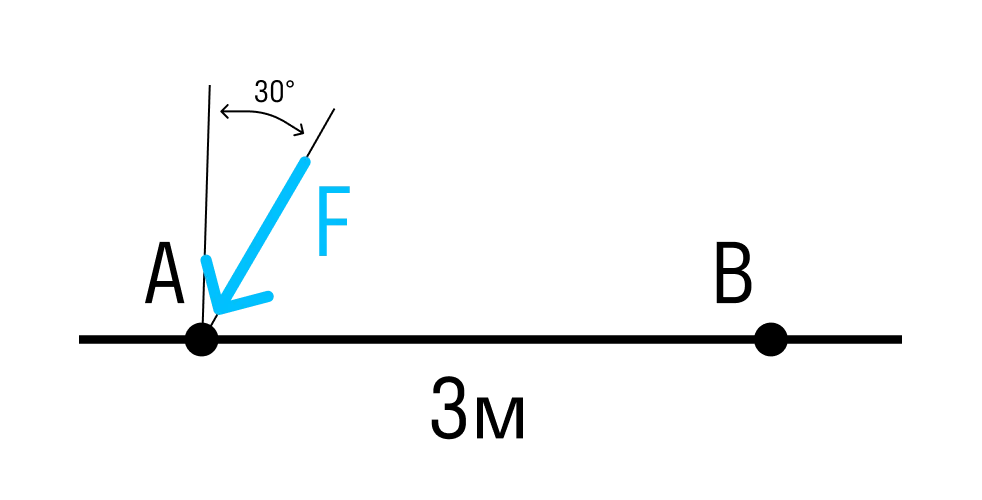
Момент силы относительно точки B:
MB=F×cos30×AB=F×cos30×3м
Если известно самое короткое расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).
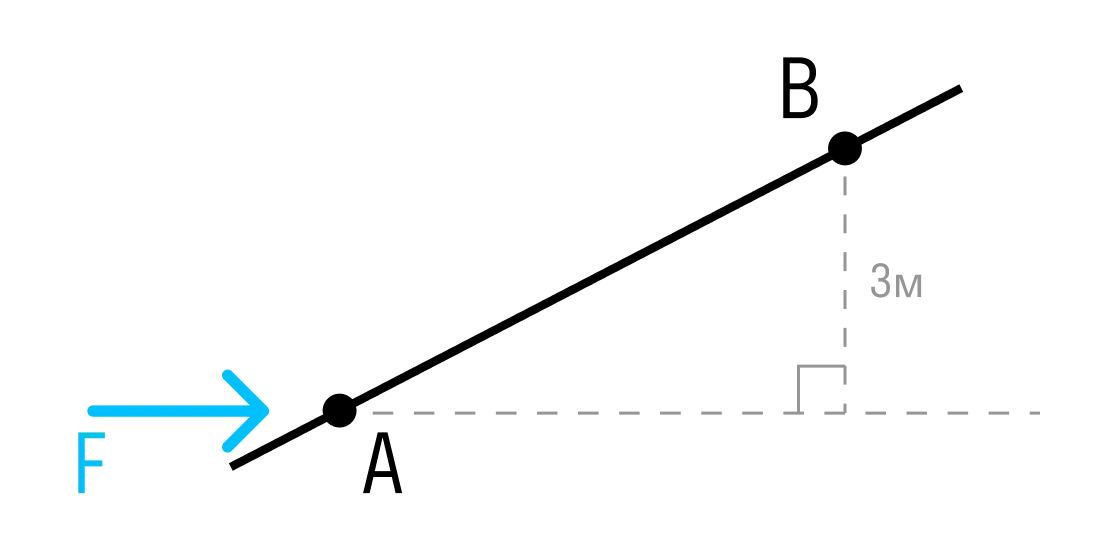
Момент силы относительно точки B:
MB=F×3м
Правило моментов
Вернемся к нашим баранам качелям. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.
Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.
Это условие выполняется относительно любой точки.
|
Правило моментов M1 + M2 +...+ Mn = M’1 + M’2 +...+ M’n M1 + M2 +...+ Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м] M’1 + M’2 +...+ M’n — сумма моментов сил, поворачивающих рычаг против часовой стрелке [Н*м] |
Давайте рассмотрим этот закон на примере задач.
Задача 1
К левому концу невесомого стержня прикреплен груз массой 3 кг.
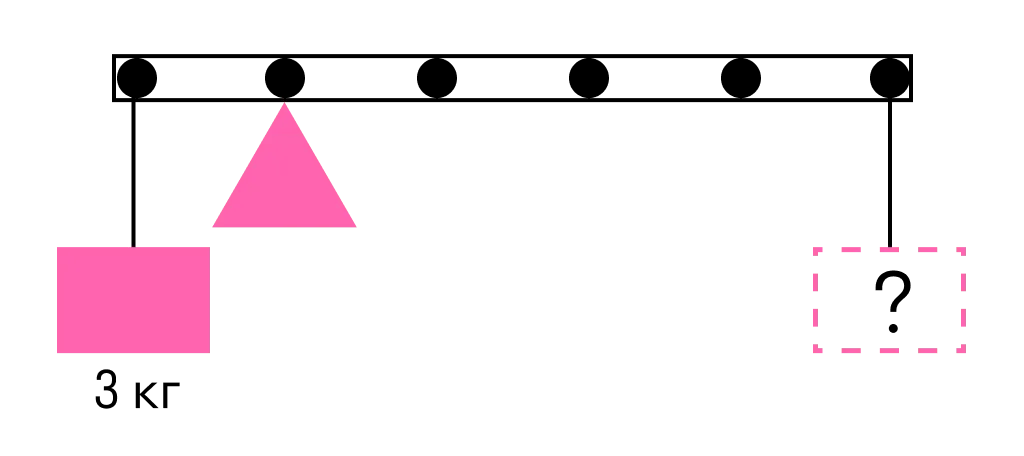
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?
Решение:
Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен
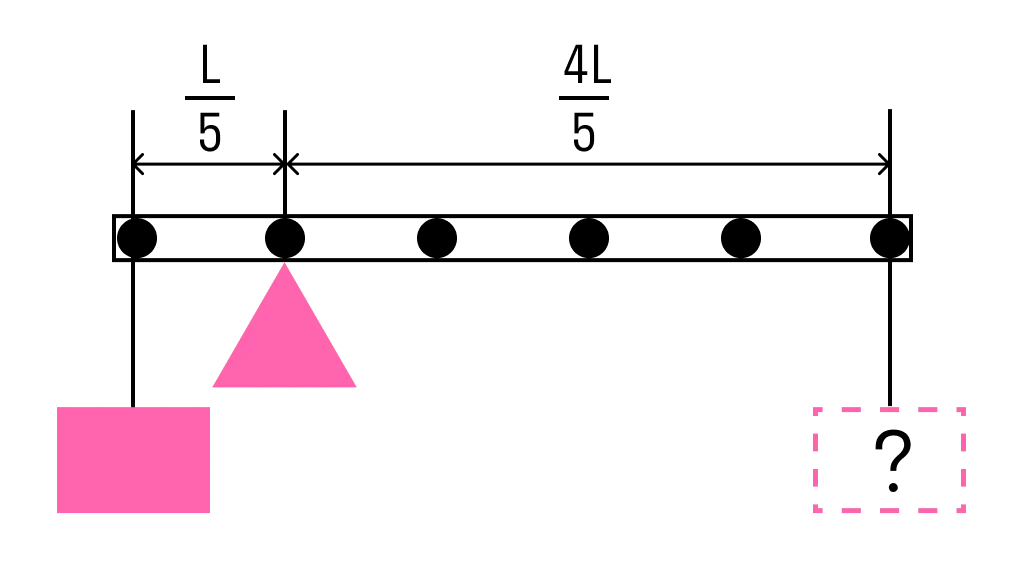
Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг
Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг
Задача 2
Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?
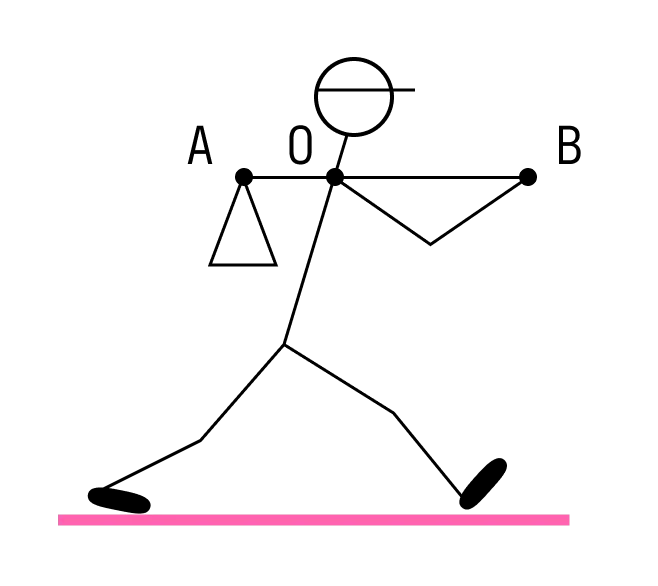
Решение:
По правилу рычага:
Ответ: расстояние ОА равно 30 см
Задача 3
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?
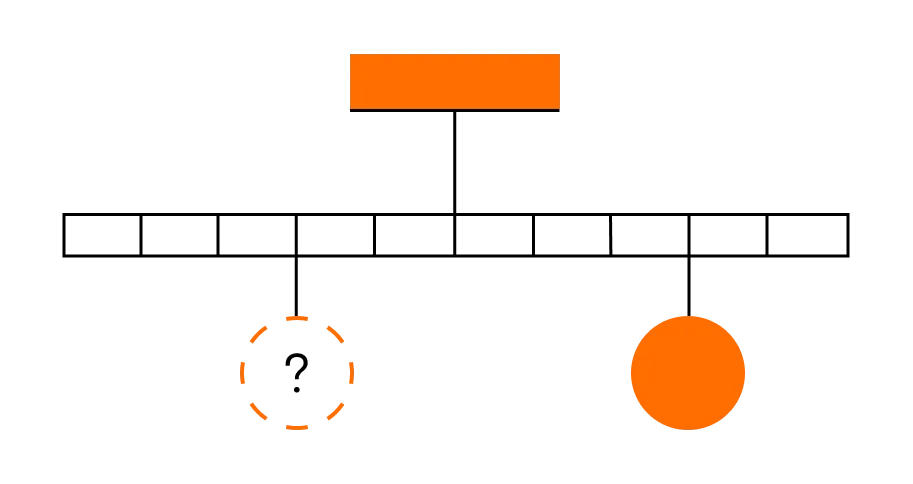
Решение:
Ответ: Масса груза равна 0,3 кг
Задача 4 — a.k.a самая сложная задачка
Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.

Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?
Решение:
Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Уточним, что 0,8 м — это расстояние от центра тяжести груза до опоры, т. е. перпендикуляр до оси вращения. Приравнивая моменты, получаем выражение для модуля силы тяжести
Ответ: модуль силы тяжести, действующей на груз равен 750 Н