Закон Кеплера

Форма Земли

Сейчас нам сложно представить, что раньше люди верили, будто Земля плоская. У греков, например, плоскость просто парила в воздухе и была окружена ледниками. А в Индии верили, что планета покоится на трех слонах, которые стоят на черепахе. Впрочем, кое-кто до сих пор так думает. Доказательств того, что наша планета на самом деле не плоская — много, но вот вам парочка, чтобы можно было поддержать светскую беседу.

Смена дня и ночи

По представлениям приверженцев плоской Земли, день и ночь сменяются, потому что Луна и Солнце вращаются над Землей — вот как-то так:

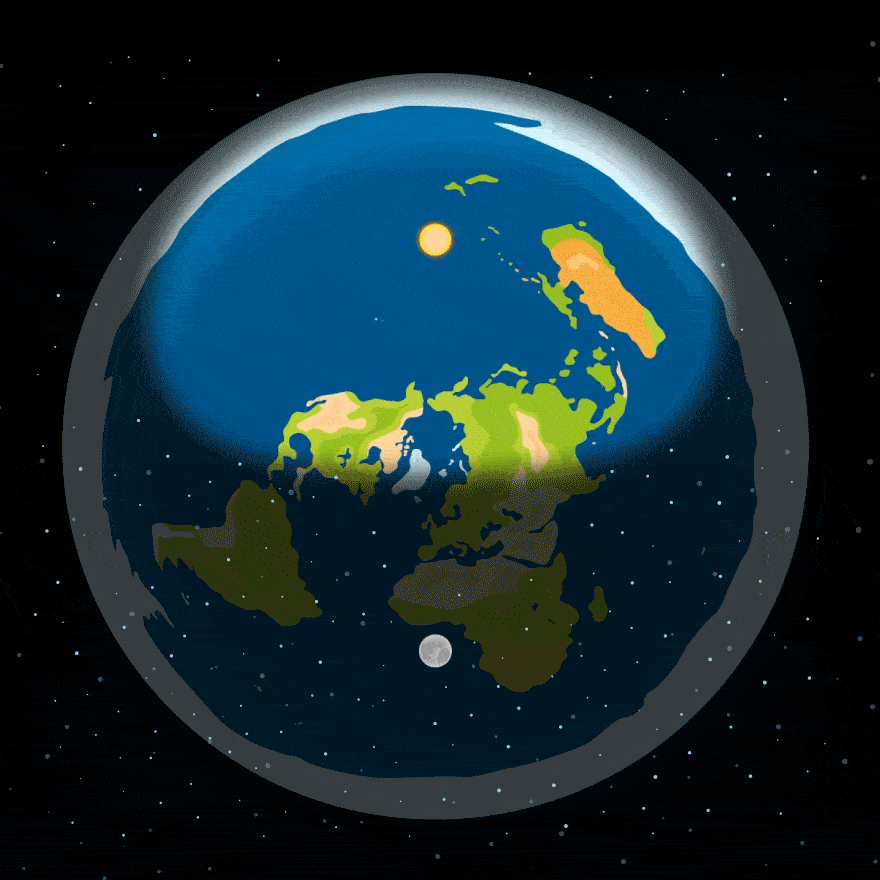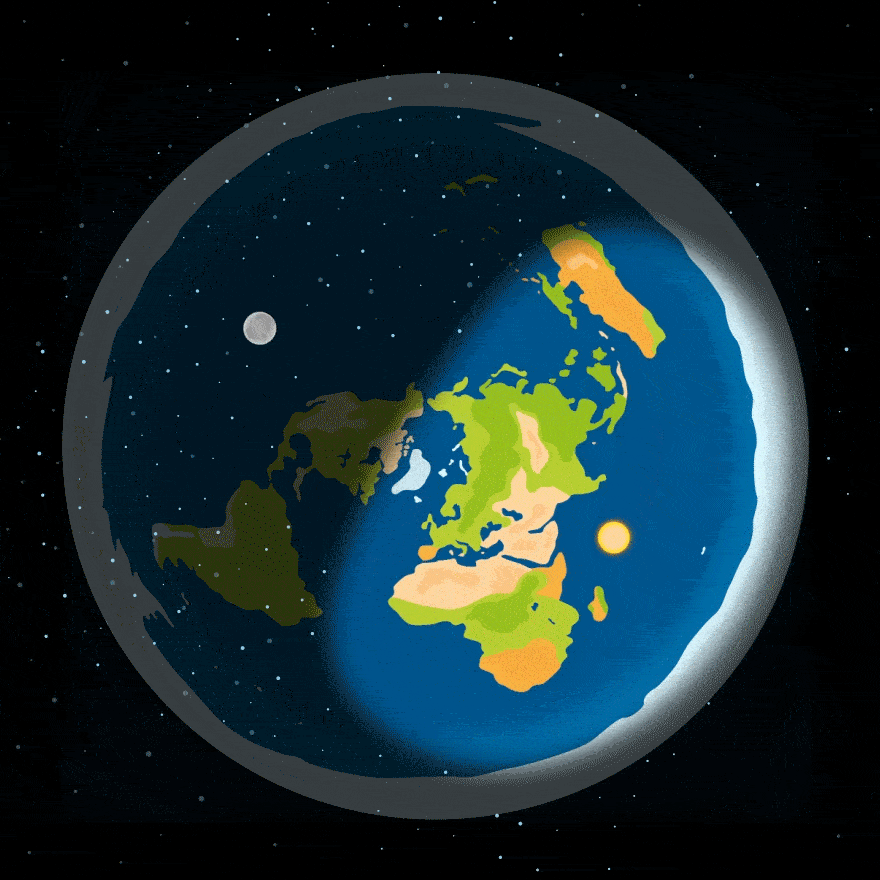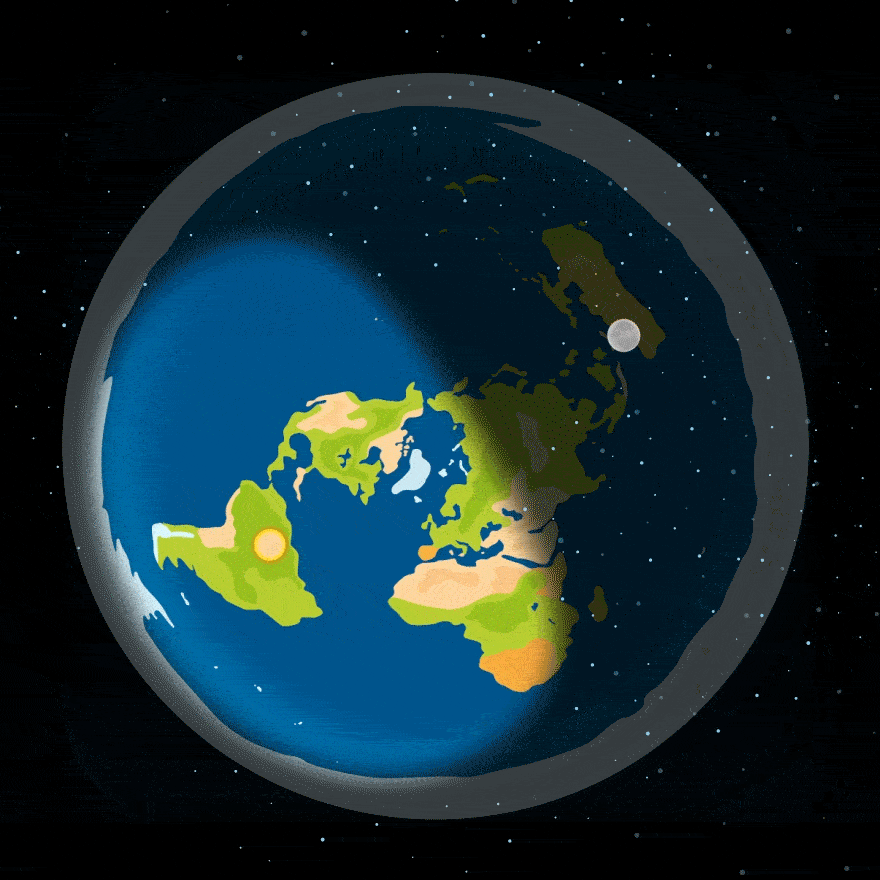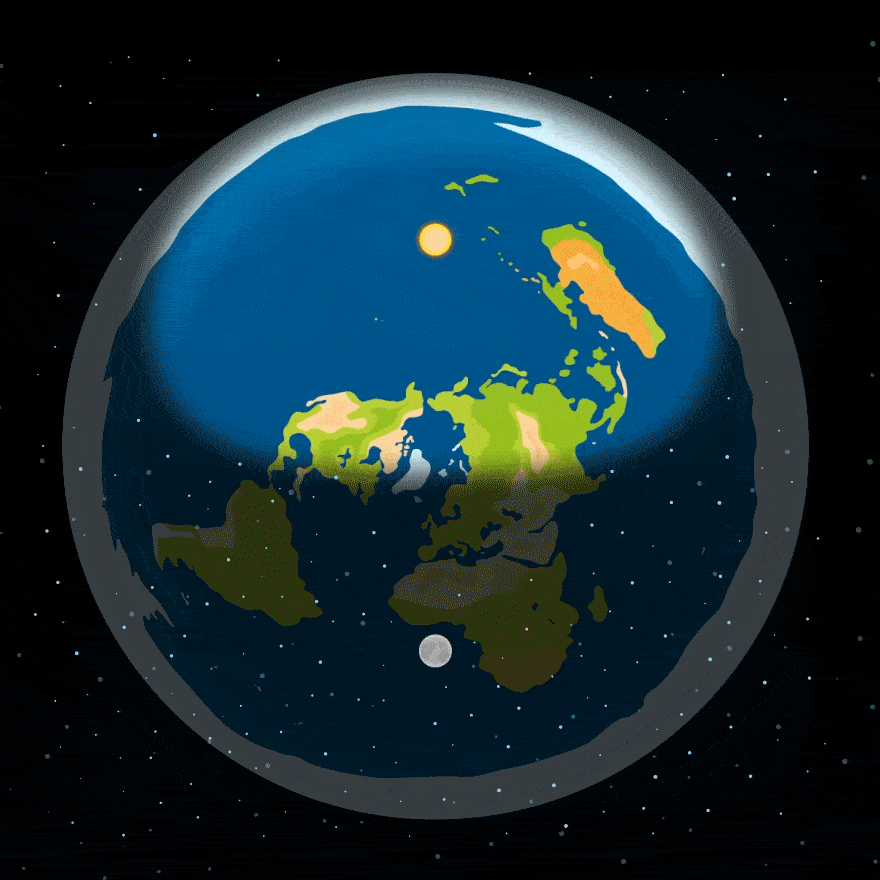
Но — упс! — эта модель вызывает целый ряд вопросов:

• Почему длина дня и ночи меняется в течение года?

• Чем объясняется цвет заката и восхода?

• Почему иногда мы можем увидеть Луну и Солнце одновременно?

• Почему Луна и Солнце не появляются каждый раз из одной и той же точки?

• Если нет гравитационного притяжения, почему они вообще крутятся?

Лунные затмения

Если Земля плоская, то непонятно, как объяснить лунные затмения. Чтобы затмение произошло, нужно, чтобы Солнце находилось по одну сторону от диска, а Луна — по другую. Тогда ломается концепция дня и ночи, которую мы описали выше, ведь день и ночь будут наступать для всей Земли одновременно.

Тени

На плоскую Землю свет от Солнца падал бы, как свет от фонаря. То есть высокие объекты в противоположном от Солнца направлении после заката оставались бы в тени.

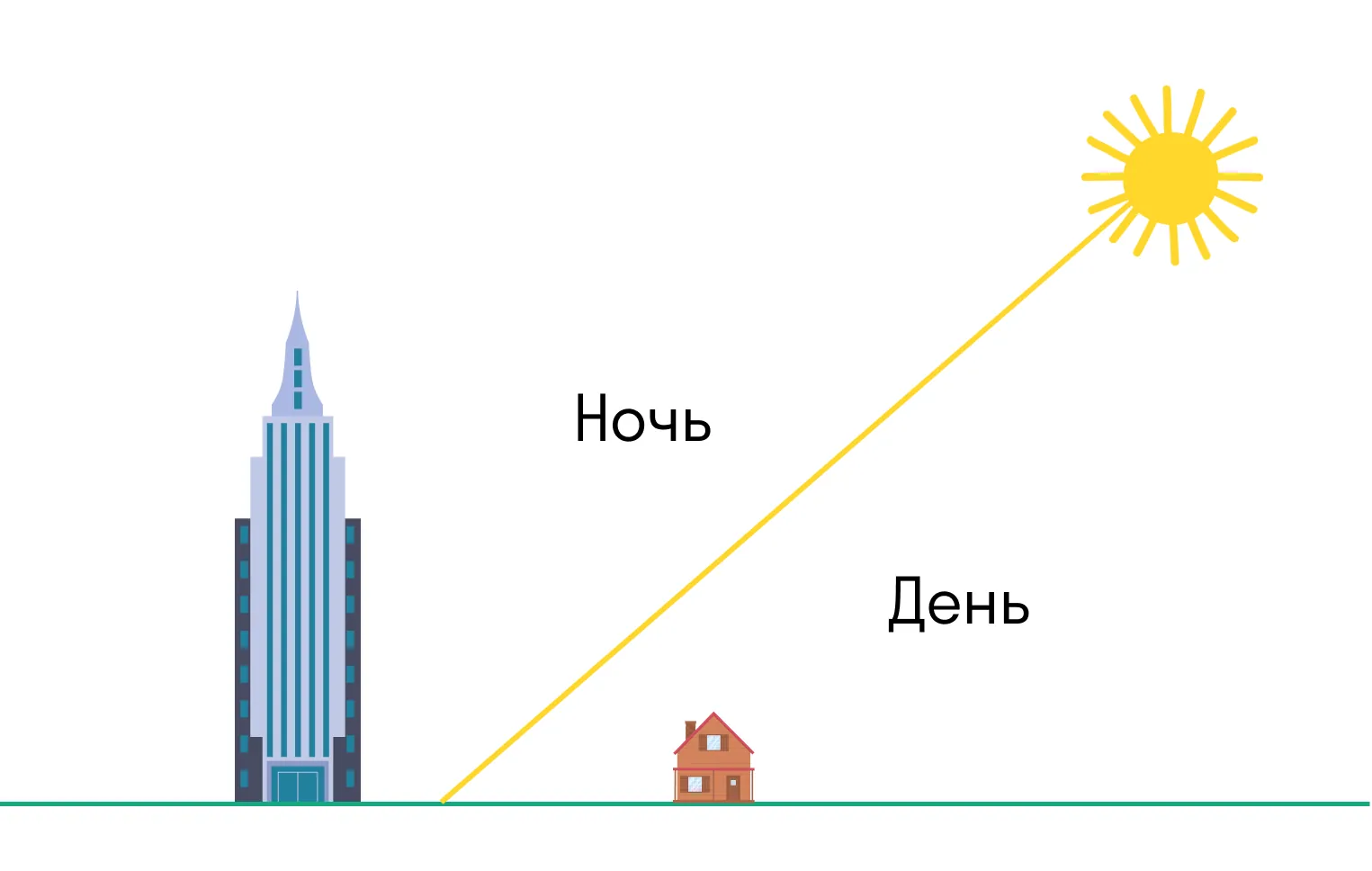
А на шарообразной Земле небоскребы или горы будут освещены Солнцем после заката или перед рассветом.

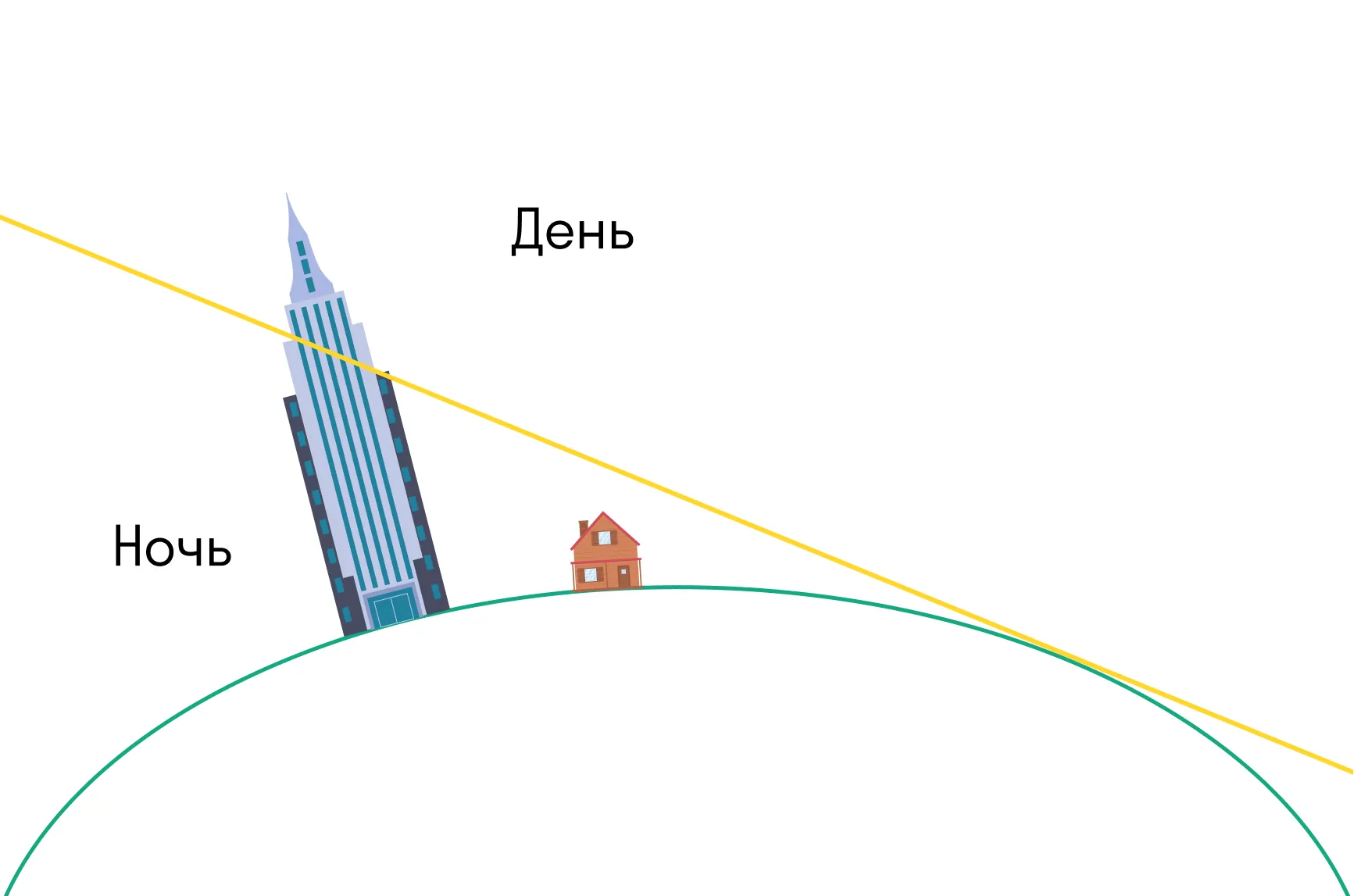
Именно это вы увидите, если застанете рассвет или закат в горах — или посмотрите на фотографии.

Окей, Земля все-таки не плоская — с этим разобрались. Но и шаром ее назвать нельзя: Земля имеет форму эллипсоида.

Эллипсоид — это такой приплюснутый шар, в одном из сечений у которого эллипс. Именно по траектории эллипса вращаются все спутники.

Эллипс

Эллипс — это замкнутая прямая на плоскости, частный случай овала. У эллипса две оси симметрии — горизонтальная и вертикальная, которые состоят из двух полуосей.

А еще у эллипса два фокуса — это такие точки, сумма расстояний от которых до любой точки P(x,y) является постоянной величиной.

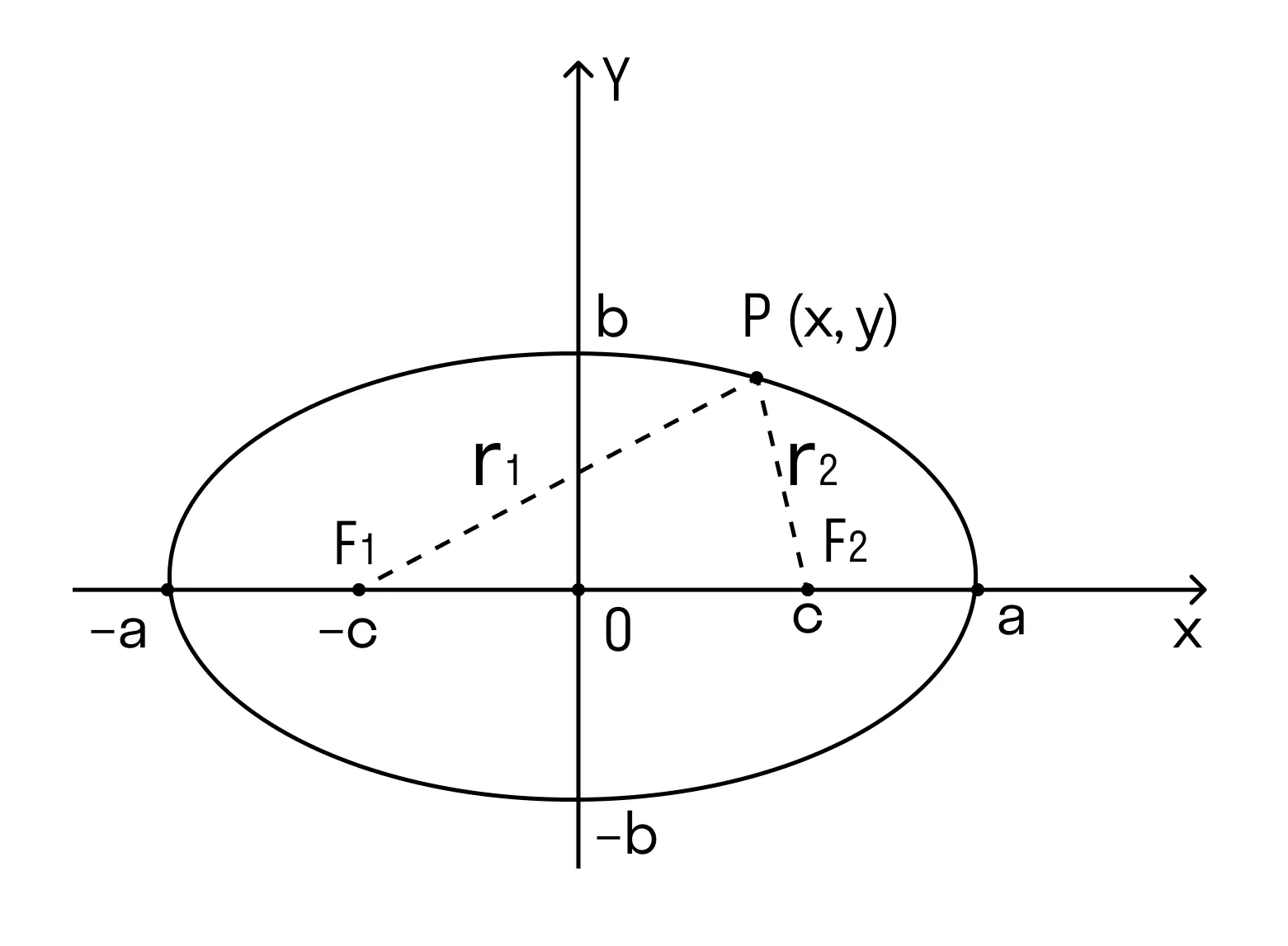
Эллипс F1 и F2 — фокусы F1 = ( c ; 0) F2 = (-c ; 0) с — половина расстояния между F1 и F2 a — большая полуось b — малая полуось r1 и r2 — фокальные радиусы

Теперь мы знаем все необходимые понятия, чтобы разобраться, в чем состоят законы Кеплера.

Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!

178.1K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подтяни оценки на курсах по физике.

• Выбирай из 890+ репетиторов по физике.

• Записывайся на бесплатные курсы для детей.

Первый закон Кеплера

Каждая планета солнечной системы вращается вокруг Солнца по эллипсоидной орбите, в одном из фокусов которого находится Солнце.

Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точка B траектории называется перигелием, а точка A, наиболее удаленная от Солнца — афелием.

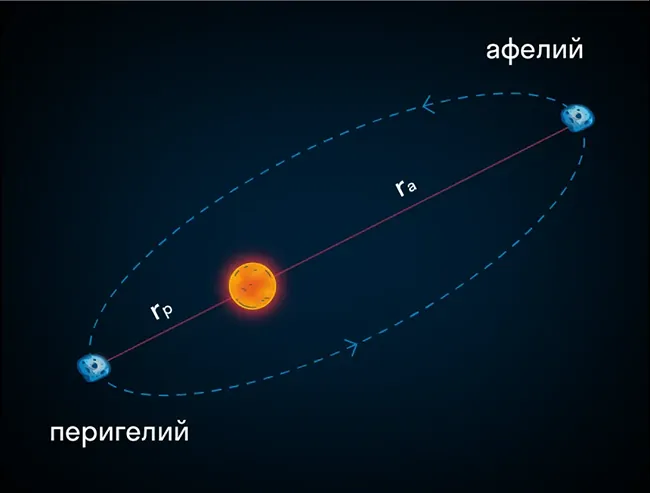
Первый закон Кеплера достаточно простой, но важный, так как в свое время он сильно продвинул астрономию. До этого открытия астрономы считали, что планеты движутся исключительно по круговым орбитам. Если же наблюдения противоречили этому убеждению, ученые дополняли главное круговое движение малыми кругами, которые планеты описывали вокруг точек основной круговой орбиты. Кеплер получил доступ к огромной базе наблюдений Тихо Браге и, изучив их, перешагнул старые идеи.

Второй закон Кеплера (закон площадей)

Радиус-вектор, соединяющий планету и Солнце, описывает в равные промежутки времени равные площади.

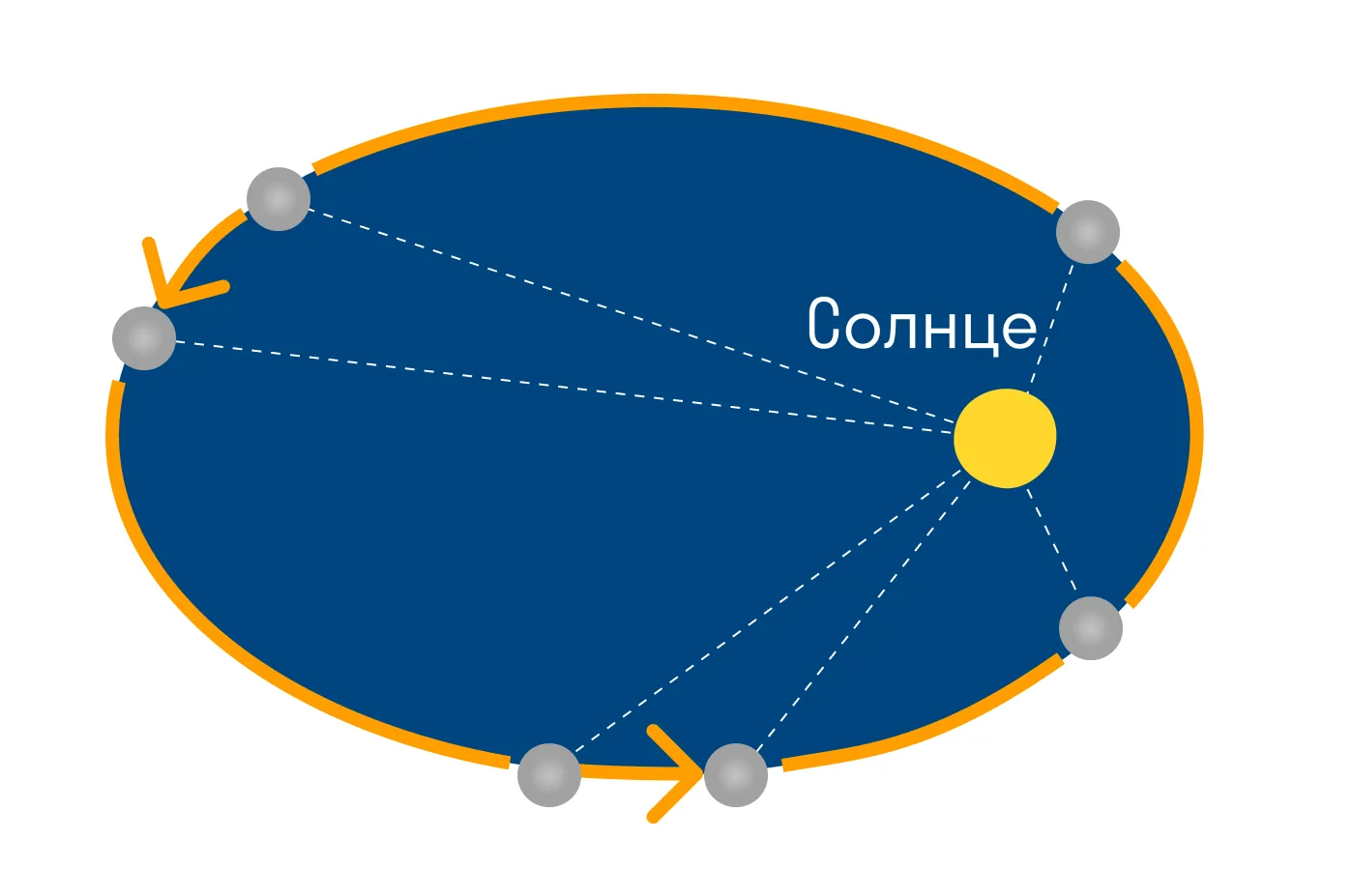
Каждая планета перемещается в плоскости, проходящей через центр Солнца. За равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади. Таким образом, тела движутся вокруг Солнца неравномерно: в перигелии они имеют максимальную скорость, а в афелии — минимальную.

На практике это можно заметить по движению Земли. Ежегодно в начале января наша планета проходит через перигелий и перемещается быстрее. Из-за этого движение Солнца по эклиптике (линии, показывающей путь Солнца по небу) также происходит быстрее, чем в другое время года. В начале июля Земля движется через афелий, из-за чего Солнце по эклиптике перемещается медленнее. Поэтому световой день летом длиннее, чем зимой.

Третий закон Кеплера

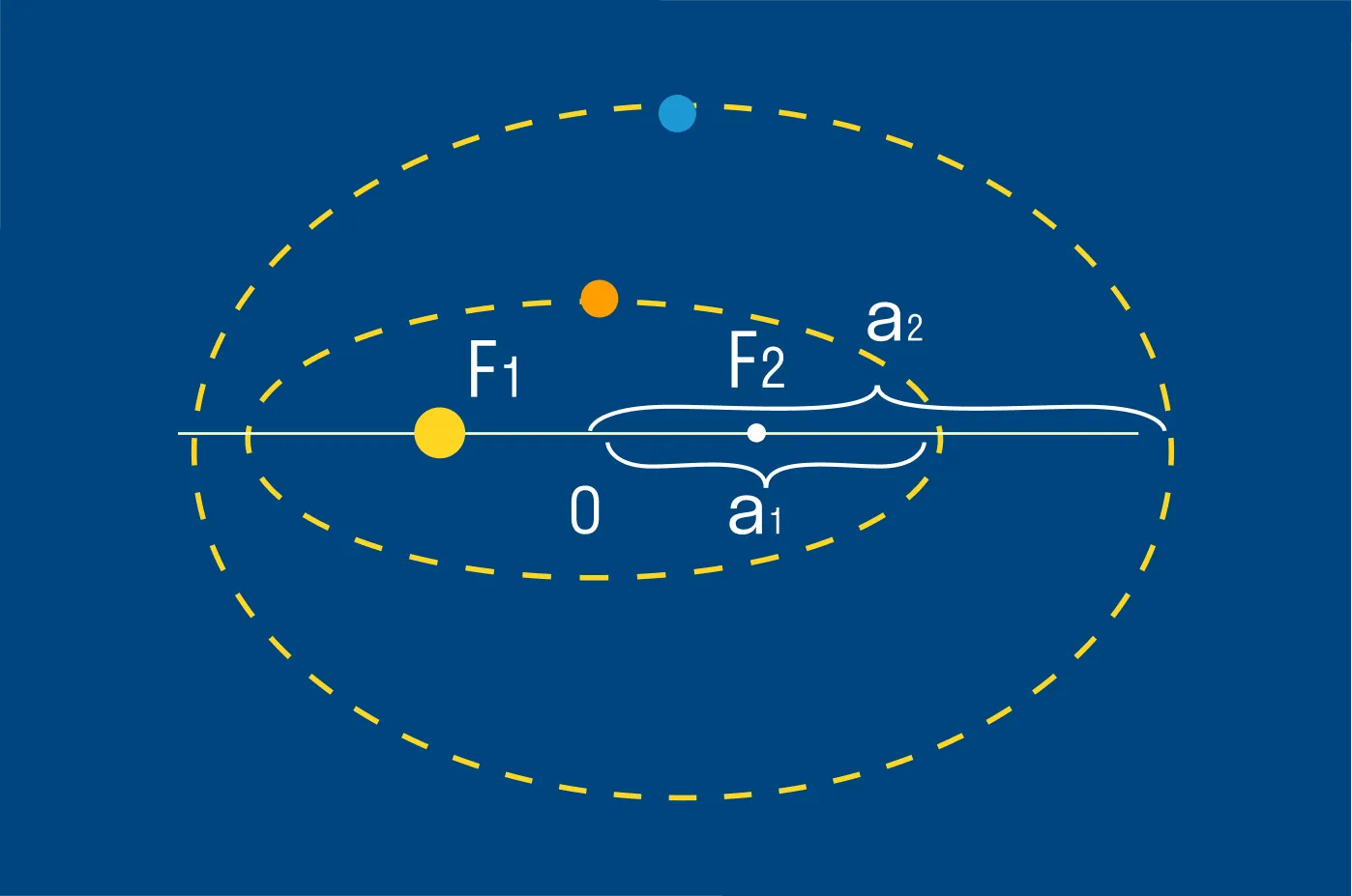
Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит.

Согласно третьему закону Кеплера, между периодом обращения планет вокруг Солнца и большими полуосями их орбит устанавливается связь. Этот закон выполняется как для планет, так и для спутников с погрешно­стью менее 1%.

Третий закон Кеплера T1 и T2 — периоды обращения двух планет [c] a1 и a2 — большие полуоси орбит планет [м]

На основании этого закона можно вычис­лить продолжительность года (времени полного оборота вокруг Солнца) любой планеты, если известно ее расстояние до Солнца в афелии.

Также можно проделать обратное — рассчитать орбиту, зная период обращения.

Закон всемирного тяготения

Законы Кеплера — это результаты наблюдений и обобщений. Впоследствии они легли в основу закона всемирного тяготения, который звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.

Формула силы тяготения согласно этому закону выглядит так:

Закон всемирного тяготения F — сила тяготения [Н] M — масса первого тела (часто планеты) [кг] m — масса второго тела [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6,67 · 10−11м3 · кг−1 · с−2

Ньютон был первым исследователем, который пришел к выводу, что между любыми телами в космосе действуют гравитационные силы, и именно они определяют характер движения этих тел.

Первая и вторая космические скорости

Законы Кеплера применимы не только к движению планет и других небесных тел в Солнечной системе, но и к движению искусственных спутников Земли и космических кораблей. В этом случае центром тяготения является Земля.

В серии книг Дугласа Адамса «‎Автостопом по Галактике»‎ говорится, что летать — это просто промахиваться мимо Земли. Чтобы промахнуться мимо Земли и стать ее искусственным спутником, нужно достичь первой космической скорости 7,9 км/с. Вот как это происходит:

Искусственный спутник Земли — космический летательный аппарат, который вращается вокруг Земли по геоцентрической орбите. Чтобы у него это получалось, аппарат должен иметь начальную скорость, которая равна или больше первой космической.

Первая космическая скорость v1 — первая космическая скорость [м/с] g — ускорение свободного падения на данной планете [м/с2] R — радиус планеты [м] На планете Земля g ≈ 10 м/с2.

Есть еще вторая и третья космические скорости. Вторая космическая скорость — это скорость, которая нужна, чтобы корабль стал искусственным спутником Солнца, а третья — чтобы вылетел за пределы солнечной системы.

Вторая космическая скорость v2 — вторая космическая скорость [м/с] g — ускорение свободного падения на данной планете [м/с2] R — радиус планеты [м] На планете Земля g ≈ 10 м/с2.