Механические колебания – это физические процессы, при которых тело или система тел периодически повторяют движение через равные интервалы времени.
Примеры:
- колебание маятника
- вибрация струны
Виды колебаний:
- свободные (маятник)
- вынужденные (работающий двигатель)
Характеристики:
- период
- частота
- амплитуда
- фаза
Механические колебания
Механические колебания — это физические процессы, точно или приблизительно повторяющиеся через одинаковые интервалы времени.
Колебания делятся на два вида: свободные и вынужденные.
Колебания, которые происходят под действием внутренних сил в колебательной системе, называют свободными. Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.
Вынужденные колебания
А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.
Какие колебания называются вынужденными?
- Вынужденные колебания – это колебания, которые происходят под действием внешней периодически меняющейся силы.
Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.
Например, качели — если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку, такое колебание будет считаться вынужденным.
Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.
Получи больше пользы от Skysmart:
-
Подтяни оценки на курсах по физике.
-
Выбирай из 890+ репетиторов по физике.
Записывайся на бесплатные курсы для детей.
Автоколебания
Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.
У автоколебательной системы есть три важных составляющих:
- сама колебательная система
- источник энергии
- устройство обратной связи, обеспечивающей связь между источником и системой
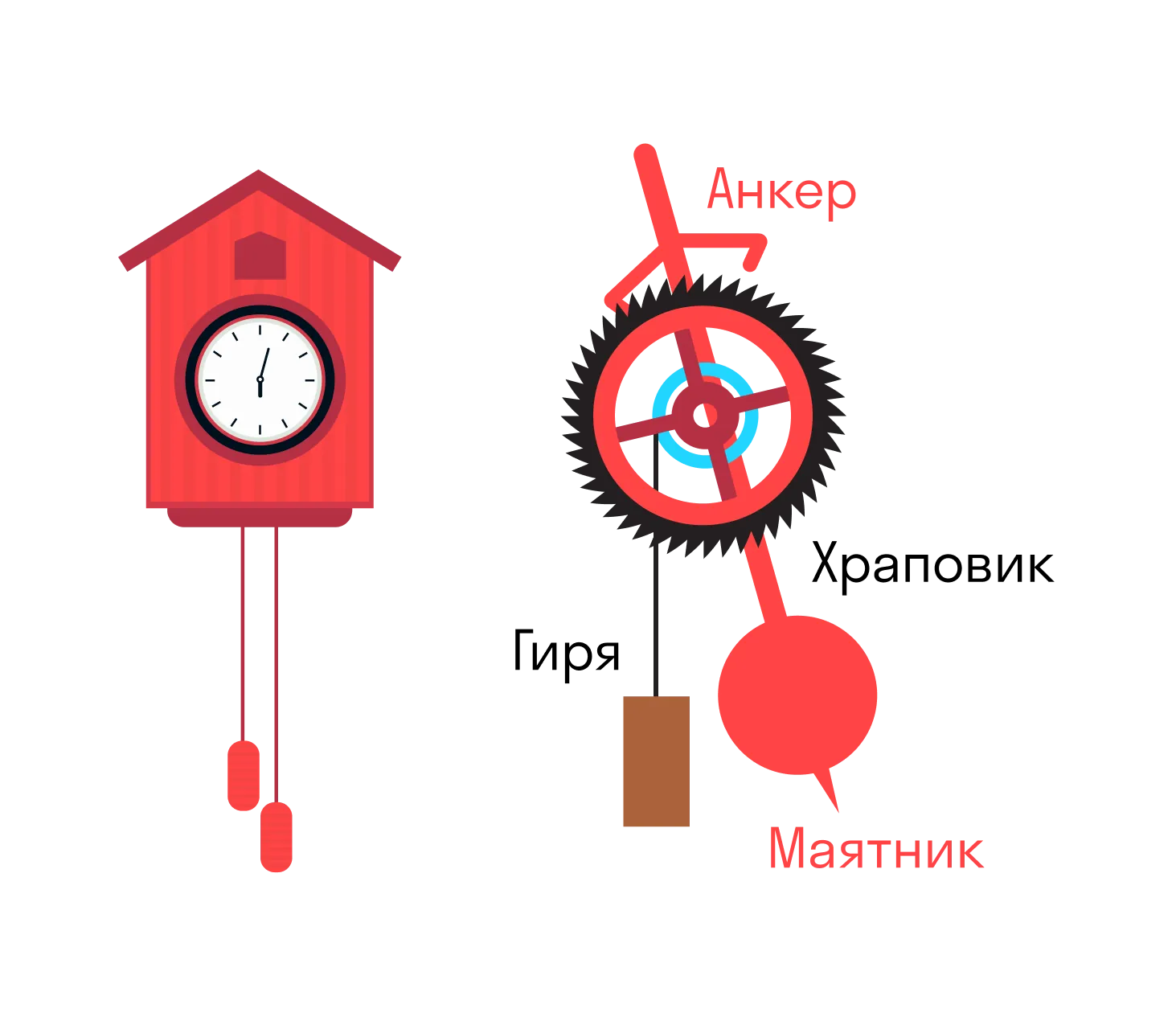
Например, часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.
Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.
Характеристики колебаний
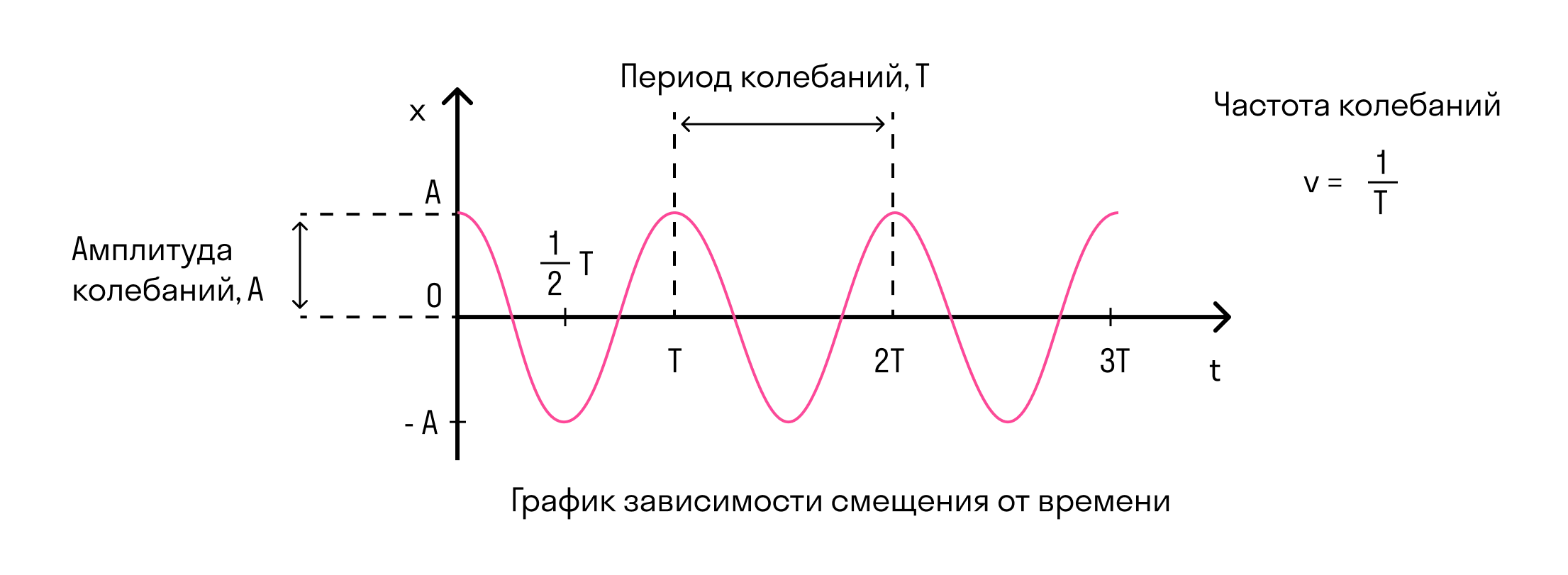
Любое колебательное движение характеризуется величинами: период, частота, амплитуда, фаза колебаний.
|
Формула периода колебаний T = t/N T — период [с] t — время [с] N — количество колебаний [-] |
Кстати, для математического и пружинного маятника есть свои формулы периода:
|
Формула периода колебания математического маятника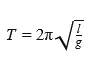 
T — период [с] l — длина нити [м] g — ускорение свободного падения [м/с^2] На планете Земля g = 9,8 м/с2 π = 3,14 |
|
Формула периода колебания пружинного маятника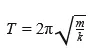 
T — период [с] m — масса маятника [кг] k — жесткость пружины [Н/м] π = 3,14 |
Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.
|
Формула частоты ν = N/t = 1/T ν — частота [Гц] t — время [с] T — период [с] N — количество колебаний [-] |
- Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо xmax.
Она используется в уравнении гармонических колебаний:
|
Уравнение гармонических колебаний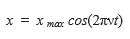 
x — координата в момент времени t [м] xmax— амплитуда [м] ν — частота [Гц] t — момент времени [с] π = 3,14 |
В данном уравнении 2πνt является фазой и обозначается греческой буквой φ.
|
Фаза колебаний φ = 2πνt φ — фаза [рад] xmax— амплитуда [м] ν — частота [Гц] t — момент времени [с] π = 3,14 |
- Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:
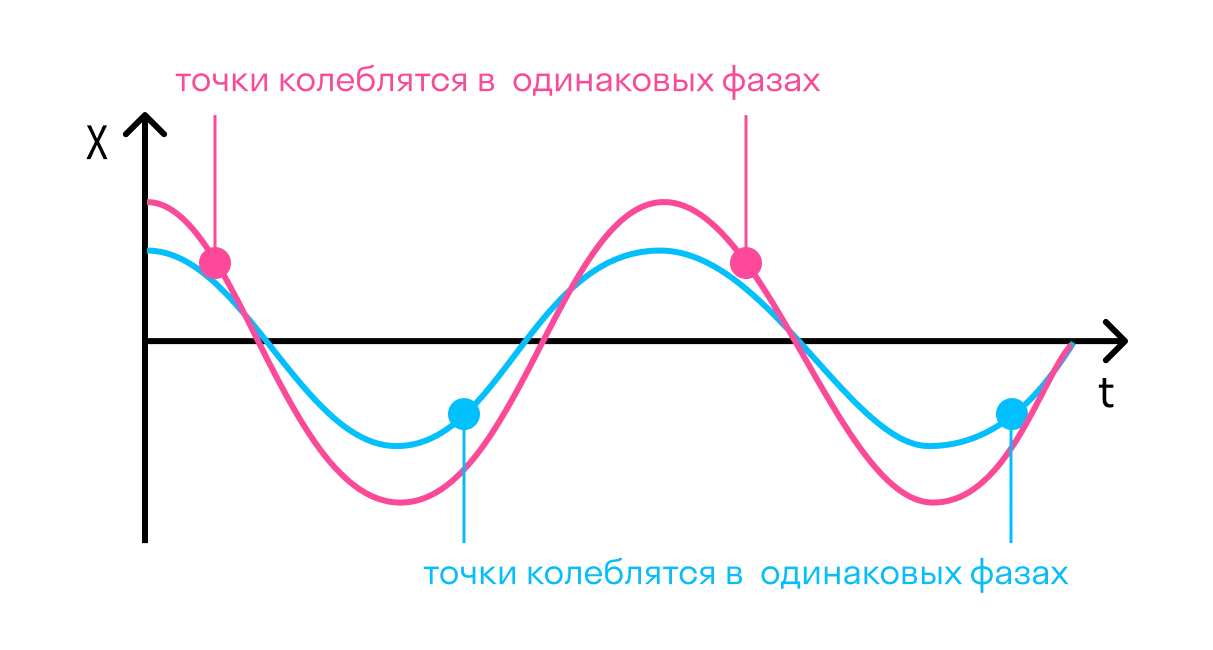
Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.
Курсы по физике за 9 класс в онлайн-школе Skysmart помогут разобраться в любой сложной теме.
