Изучайте английский в любое время, в любом месте

Задание с развернутым ответом

Выполните его и проверьте ответ по критериям ФИПИ

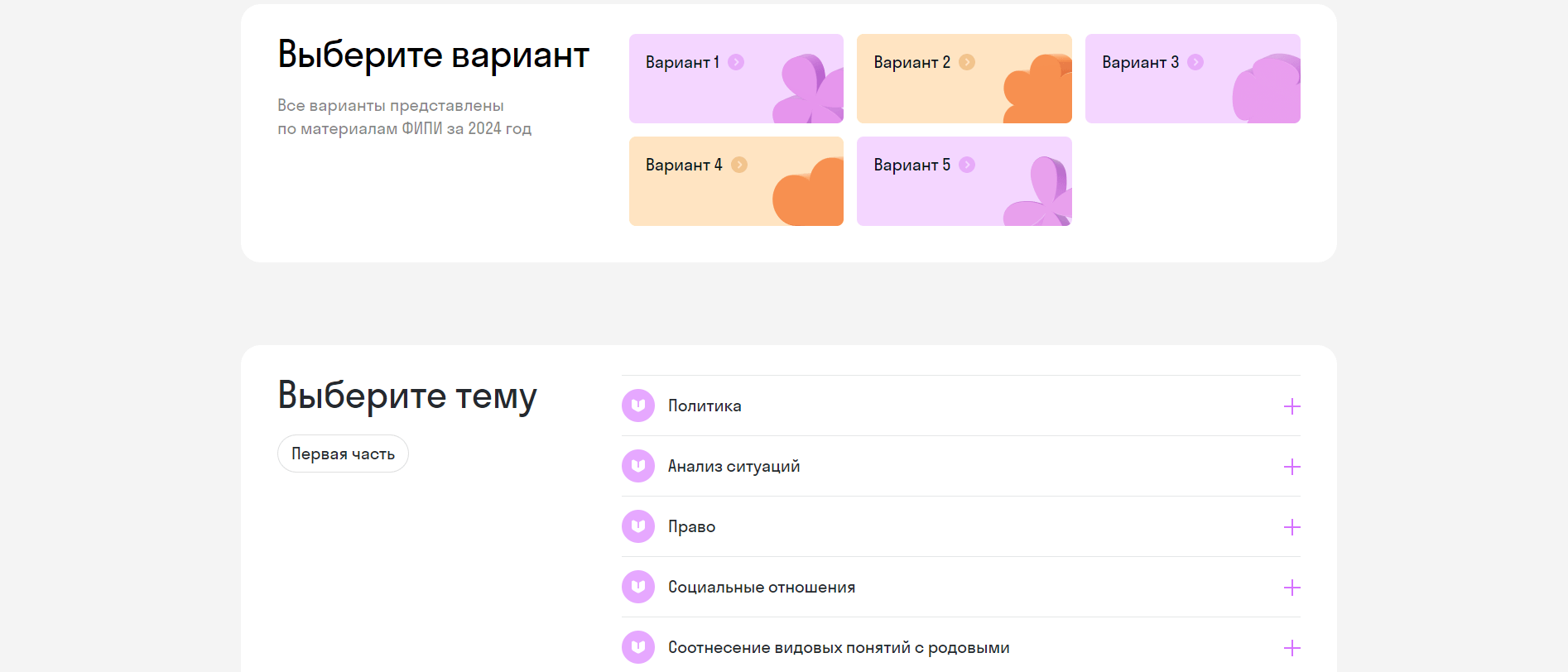
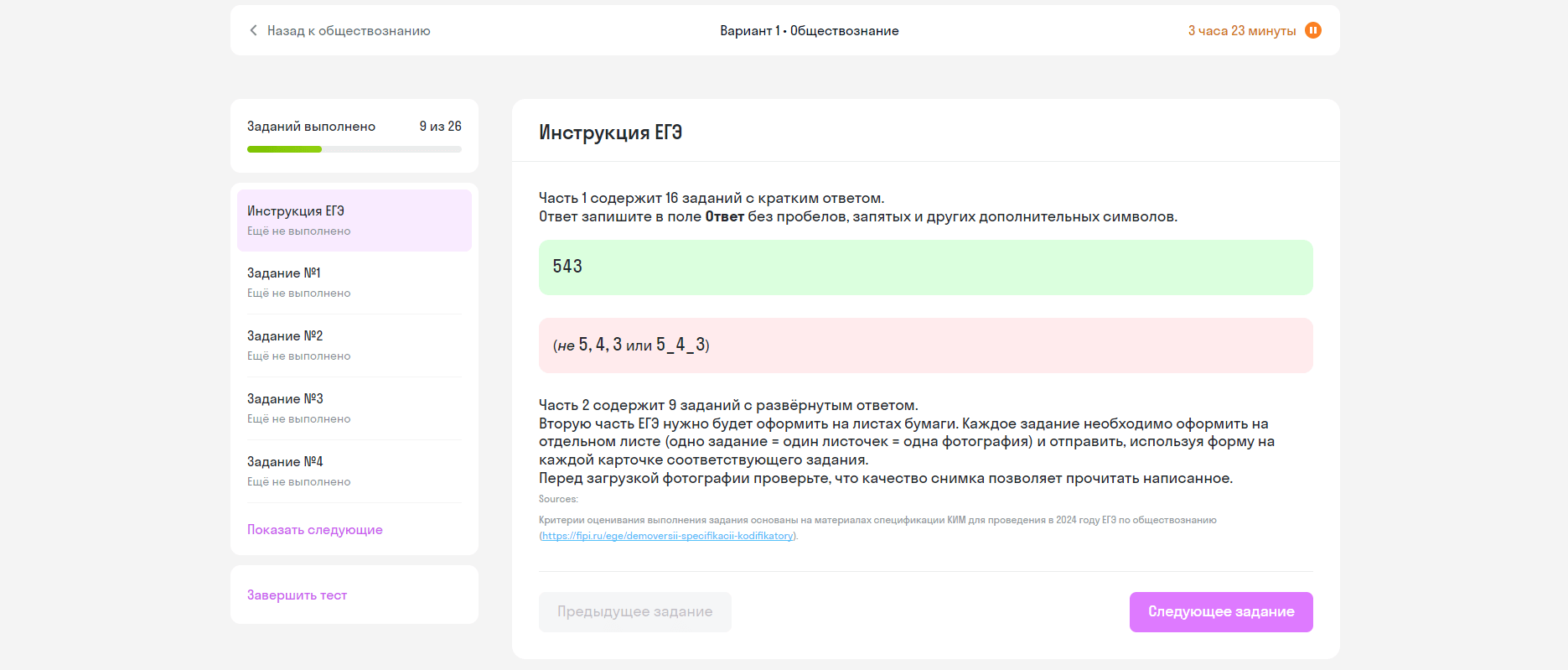
Все рёбра правильной шестиугольной призмы MNPKTGM_1N_1P_1K_1T_1G_1 равны 6\sqrt{14}. Найди расстояние от точки G до прямой TK_1.

Построим плоскость, проходящую через точку G и прямую TK_1. Соединим эти три точки.

Затем в плоскости M_1K_1T_1 проведем прямую, K_1M_1 параллельную GT (т.к. плоскости основания параллельны).

Затем соединим точки M_1G.

Обозначим полученную плоскость буквой \alpha.

Будем искать перпендикуляр из точки G на прямую TK_1 в плоскости \alpha.

Продлим боковые стороны трапеции до пересечения в точке E. Т.к. призма прямая и правильная, то трапеция M_1GTK_1 — равнобокая.

Следовательно, треугольник M_1EK_1 — равнобедренный, следовательно, EH_1 — медиана и высота.

ET=TK_1=12\sqrt{7}=GE=M_1G (как диагональ квадрата TT_1KK_1).

GT=6\sqrt{14}

Следовательно, H_1T=\dfrac{GT}{2}=3\sqrt{14}

EH_1=\sqrt{ET^2-H_1T^2}=3\sqrt{98}

S_{GTE}=\dfrac{1}{2} \cdot EH_1 \cdot GT=126\sqrt{7}

S_{GTE}=\dfrac{1}{2} \cdot GH \cdot ET=6\sqrt{7} \cdot GH

GH=21

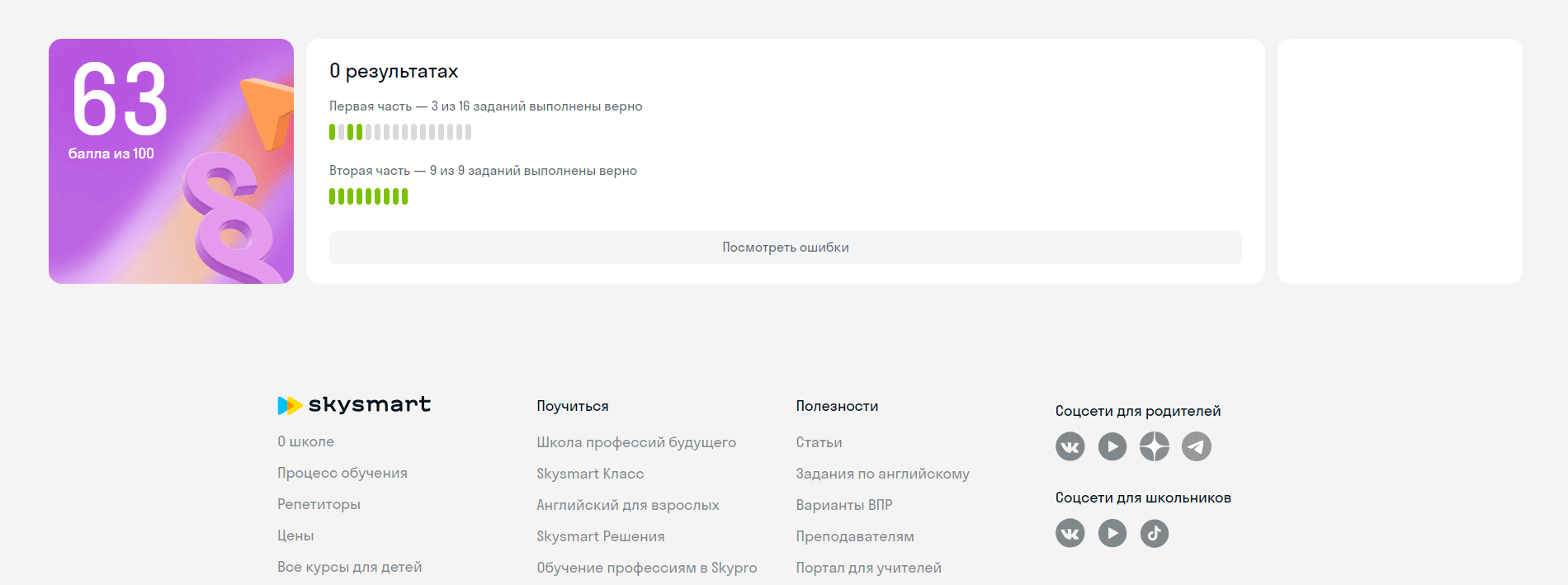
2 балл	Если обоснованно получен верный ответ
1 балл	Если обоснованно получен ответ, отличающийся от верного исключением точек или получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения
0 баллов	Если решение не соответствует ни одному из критериев, перечисленных выше

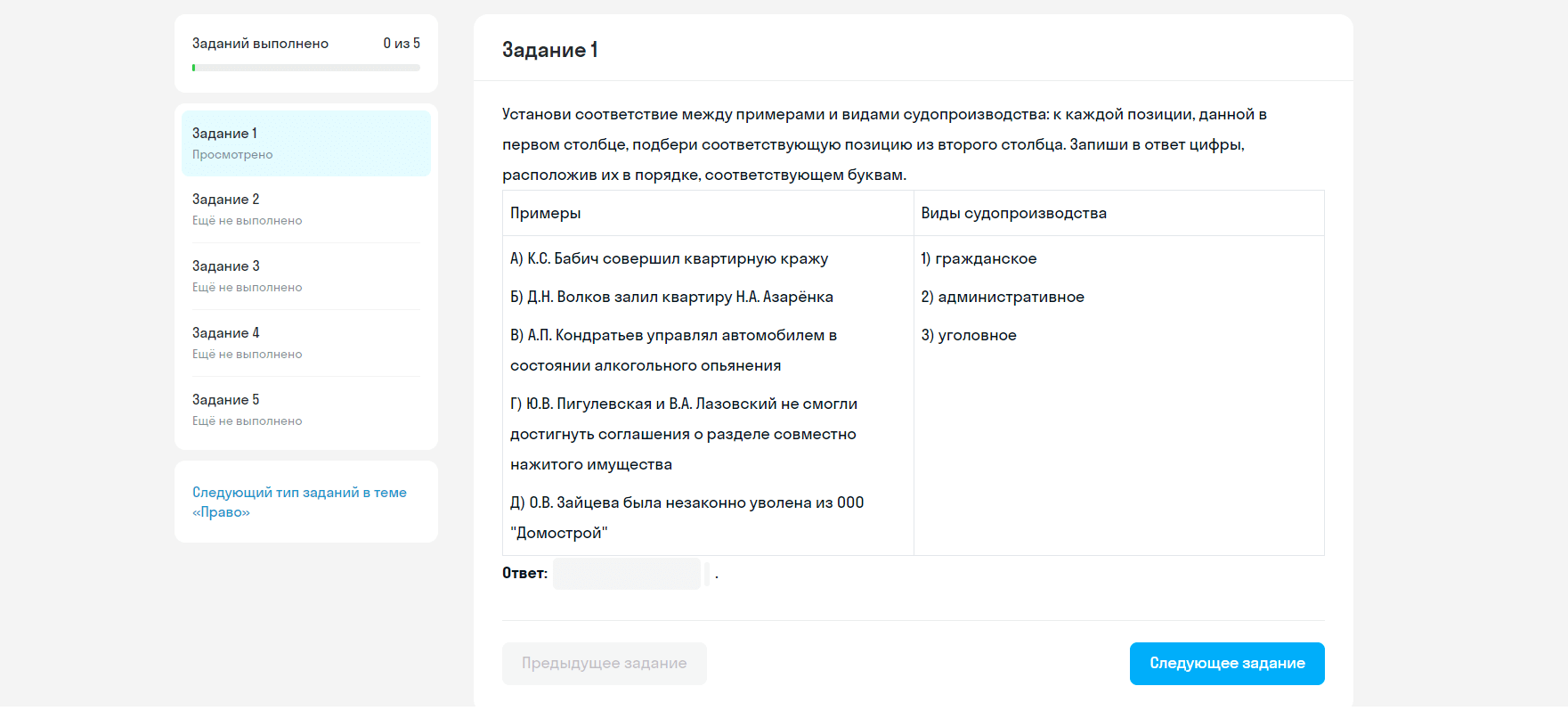
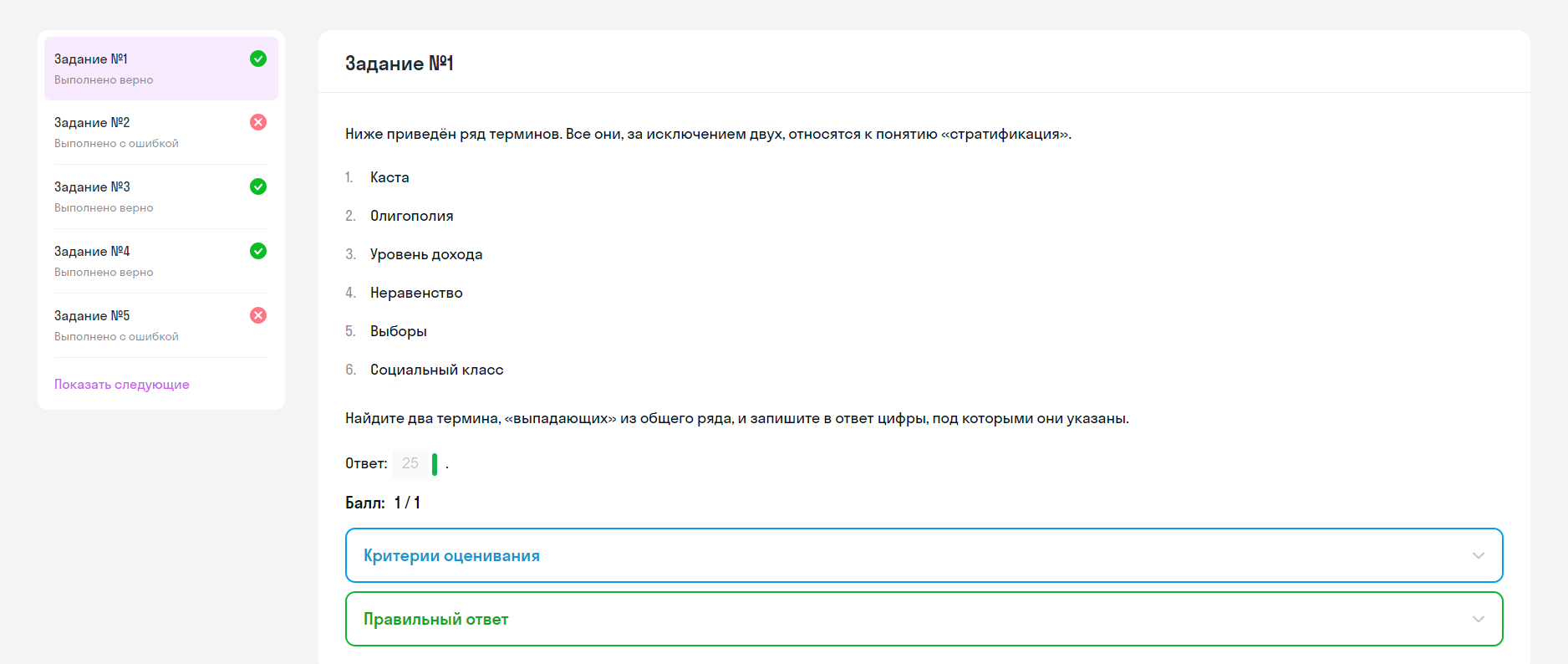
Дана правильная четырёхугольная призма SPQTS_1P_1Q_1T_1, точки E и F лежат на рёбрах так, что T_1E:ET=4:3, Q_1F:FQ=1:6.

а) Докажи, что плоскость SFE параллельна прямой PT.

Подтвердите выполнение задания: Выполнил Не выполнил

б) Найди расстояние между точкой T и плоскостью SFE, если известно, что ST=12\sqrt{2}, SS_1=14\sqrt{3}.

а) Построение сечения призмы плоскостью SFE:

1) SE, EF

2) FZ \parallel SE

3) SZ \parallel FE

Обозначим T_1E=4x, ET=3x, FQ_1=x, FQ=6x, QQ_1=7x

Проведём ZB \parallel PQ

ZF \parallel SE, следовательно, FB=ET

FB=3x, следовательно, BQ=QQ_1-Q_1F-FB=7x-x-3x=3x

следовательно, ZP=EТ=3x

следовательно, ZE \parallel PT, следовательно, SFE \parallel PT

б) Метод объёмов.

V_{STEZ}=\dfrac{1}{3}\cdot S_{SZE} \cdot h_1

h_1 — высота пирамиды STEZ, проведённая из вершины T, следовательно, эта высота — искомая в задаче

V_{STEZ}=\dfrac{1}{3}\cdot S_{SET}\cdot h_2

h_2 — высота пирамиды STEZ, проведённая из вершины Z.

ET = \dfrac{3}{7}\cdot TT_1= \dfrac{3}{7} \cdot 14\sqrt{3}=6\sqrt{3}

SE=\sqrt{ST^2+ET^2}=6\sqrt{11}

ZE=PT=12\sqrt{2}\cdot \sqrt{2}

S_{SZE}=\dfrac{1}{2}\cdot h_3 \cdot EZ

h_3 — высота равнобедренного треугольника SZE, проведённая к стороне ZE

h_3=\sqrt{(6\sqrt{11})^2-12^2}=6\sqrt{7}

S_{SZE}=\dfrac{1}{2} \cdot 6\sqrt{7} \cdot 24=72\sqrt{7}

S_{SET}=\dfrac{1}{2}\cdot ST \cdot TE=36\sqrt{6}

h_2=SP=ST=12\sqrt{2}

V_{STEZ}=\dfrac{1}{3}\cdot S_{SET}\cdot h_2=288\sqrt{3}

V_{STEZ}=\dfrac{1}{3}\cdot S_{SZE}\cdot h_1

h_1=\dfrac{3V_{STEZ}}{S_{SZE}}=\dfrac{12\sqrt{21}}{7}

2 балл	Если обоснованно получен верный ответ
1 балл	Если обоснованно получен ответ, отличающийся от верного исключением точек или получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения
0 баллов	Если решение не соответствует ни одному из критериев, перечисленных выше

В правильной шестиугольной призме ABCDEFA_1B_1C_1D_1E_1F_1 сторона основания равна 1, а высота равна 2. Найди расстояние от точки A до прямой CD_1.

\sqrt3

2 балл	Если обоснованно получен верный ответ
1 балл	Если обоснованно получен ответ, отличающийся от верного исключением точек или получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения
0 баллов	Если решение не соответствует ни одному из критериев, перечисленных выше

Как пользоваться тренажёром

Инструкция

Сперва выберите предмет: обществознание, русский язык, базовую или профильную математику. Далее — формат. Это могут быть задания по конкретной теме или полноценный пробный экзамен со всеми типами заданий и темами по кодификатору.

Первое поможет тогда, когда надо отточить задания лишь по нескольким разделам программы. Выполнять весь тест для этого не нужно. Вместо этого можно выбрать раздел и темы внутри него, чтобы отработать все типы заданий, которые могут попасться на экзамене.

Переключаться между ними можно через кнопку Следующий тип заданий в теме.

Если же остановиться на пробном экзамене, можно будет выбрать один из нескольких вариантов. Далее тренажёр ознакомит вас со всеми условиями пробника: сколько будет заданий и какого типа, что понадобится для выполнения.

Обратите внимание: пробный экзамен в тренажёре повторяет условия реального. А значит, это работа на время, которое будет отсчитывать таймер. Если нужно, во время работы можно будет поставить таймер на паузу. Пока она активна, все задания на экране будут скрыты.

В начале пробника всегда будет инструкция. Она напомнит, какие бывают типы заданий в ЕГЭ, чем они отличаются. А также научит добавлять ответы в тренажёр, чтобы тот правильно их обработал.

Слева — все задания пробника по порядку. Их можно переключать здесь же или нажатием кнопки Следующее задание. Как и на реальном экзамене, задания можно выполнять по очереди или в произвольном порядке. С последним помогут кнопки Показать следующие и Показать предыдущие.

Если задание даётся трудно, перейдите к следующему. Позже можно будет вернуться к пропущенным, если останется время. По окончании теста можно не дожидаться, пока сработает таймер, и нажать Завершить тест. Тогда тренажёр перейдёт к проверке результатов.

Разбор результатов начинается со 2 части пробника. Здесь вы сможете сами сравнить ответ с верным и выставить количество баллов. Это несложно — на той же странице мы понятным языком изложили все критерии оценивания.

После этого тренажёр покажет, сколько баллов вы набрали за экзамен. Здесь же будет видно, в какой части и номерах были ошибки. Разобрать их точнее можно с помощью кнопки под результатами.

В разделе с разбором ошибок можно сверить свои ответы из 1 части экзамена с правильными. Это поможет закрепить знания по теме и не ошибиться в следующий раз.

Удачи и высоких баллов!

Расстояние от точки до прямой и до плоскости: задания и теория

Как пользоваться тренажёром

Инструкция