Изучайте английский в любое время, в любом месте

Задание с развернутым ответом

Выполните его и проверьте ответ по критериям ФИПИ

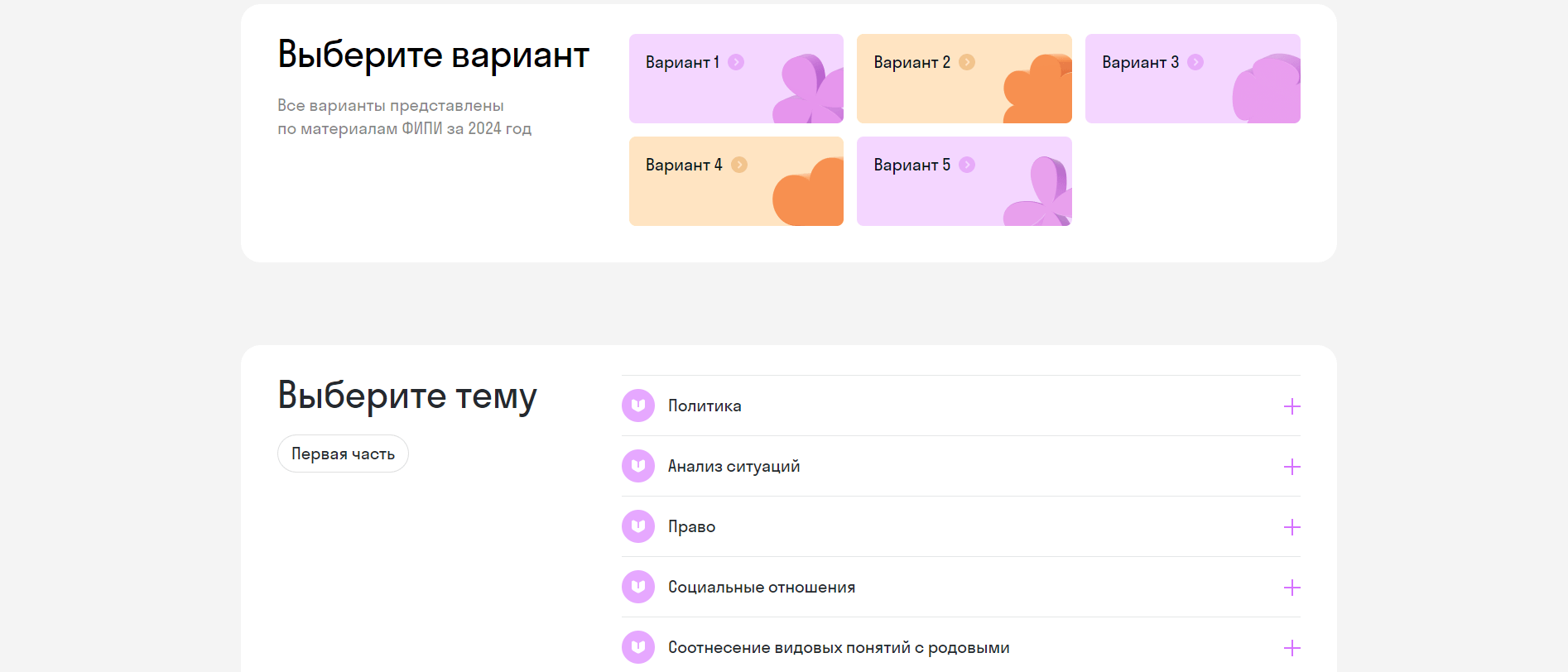
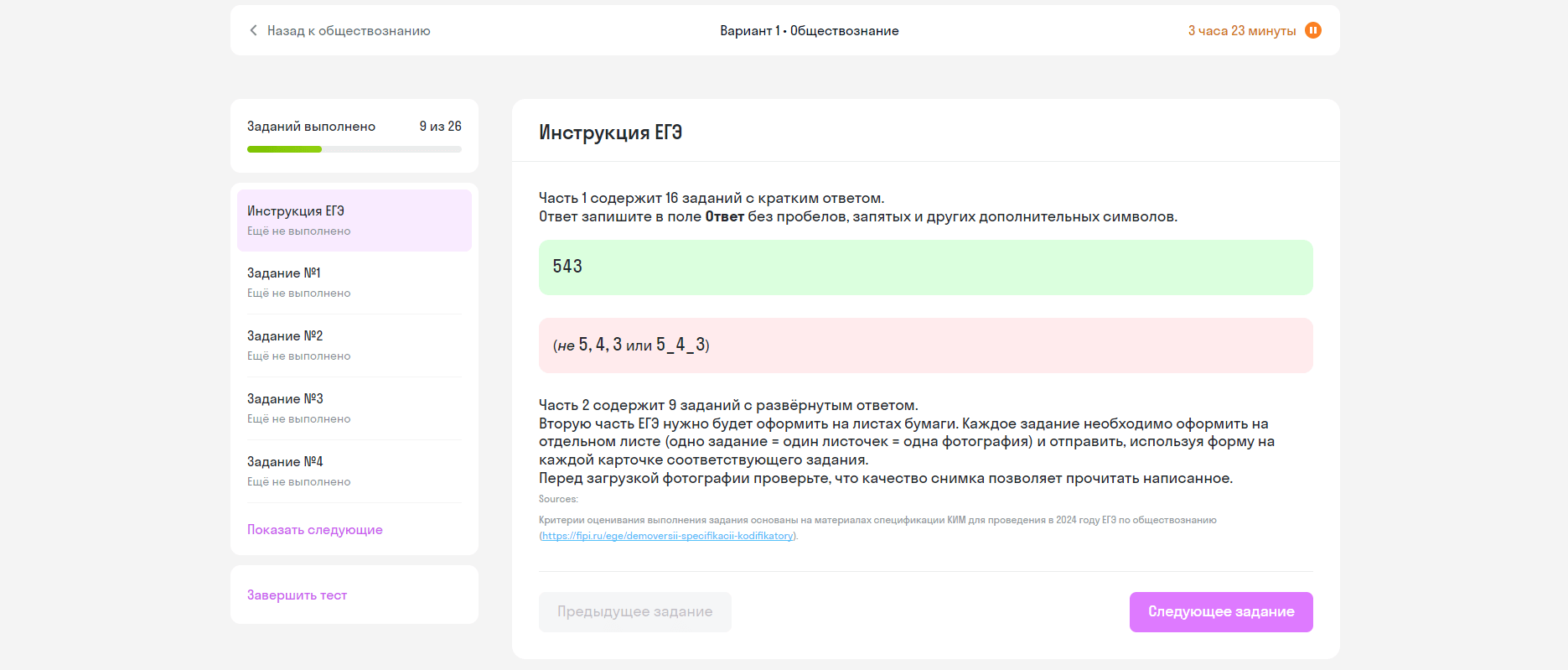
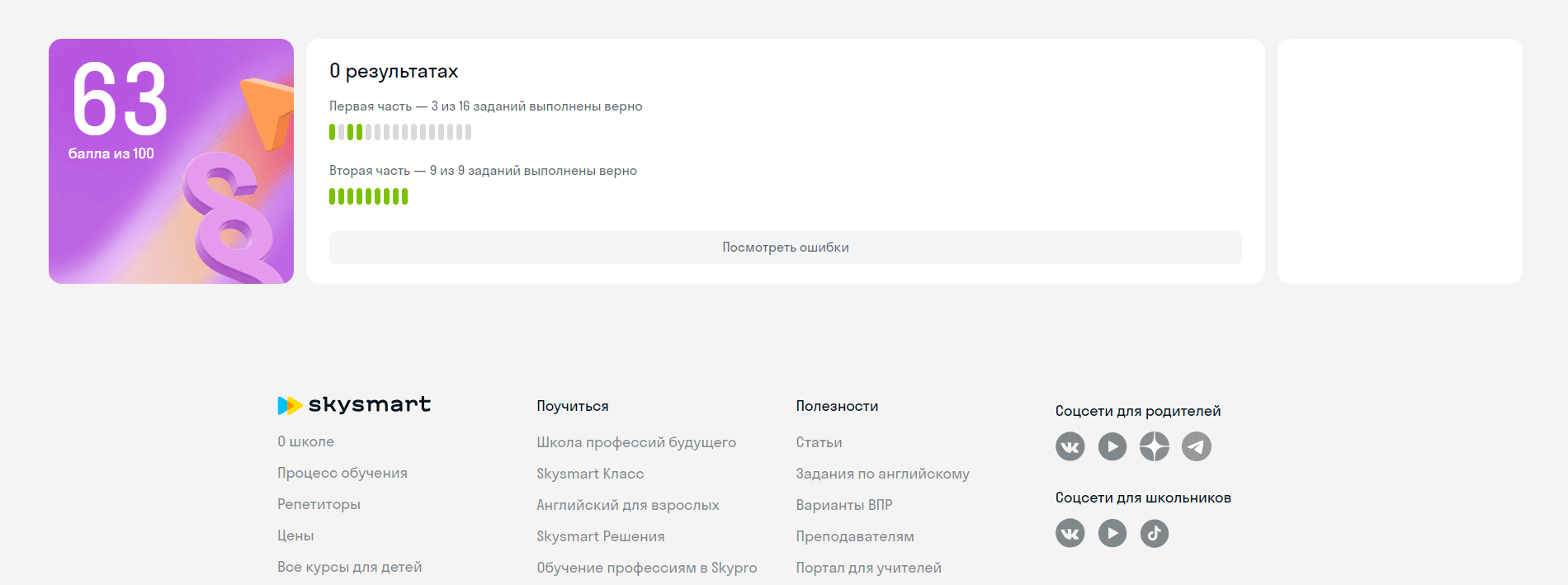
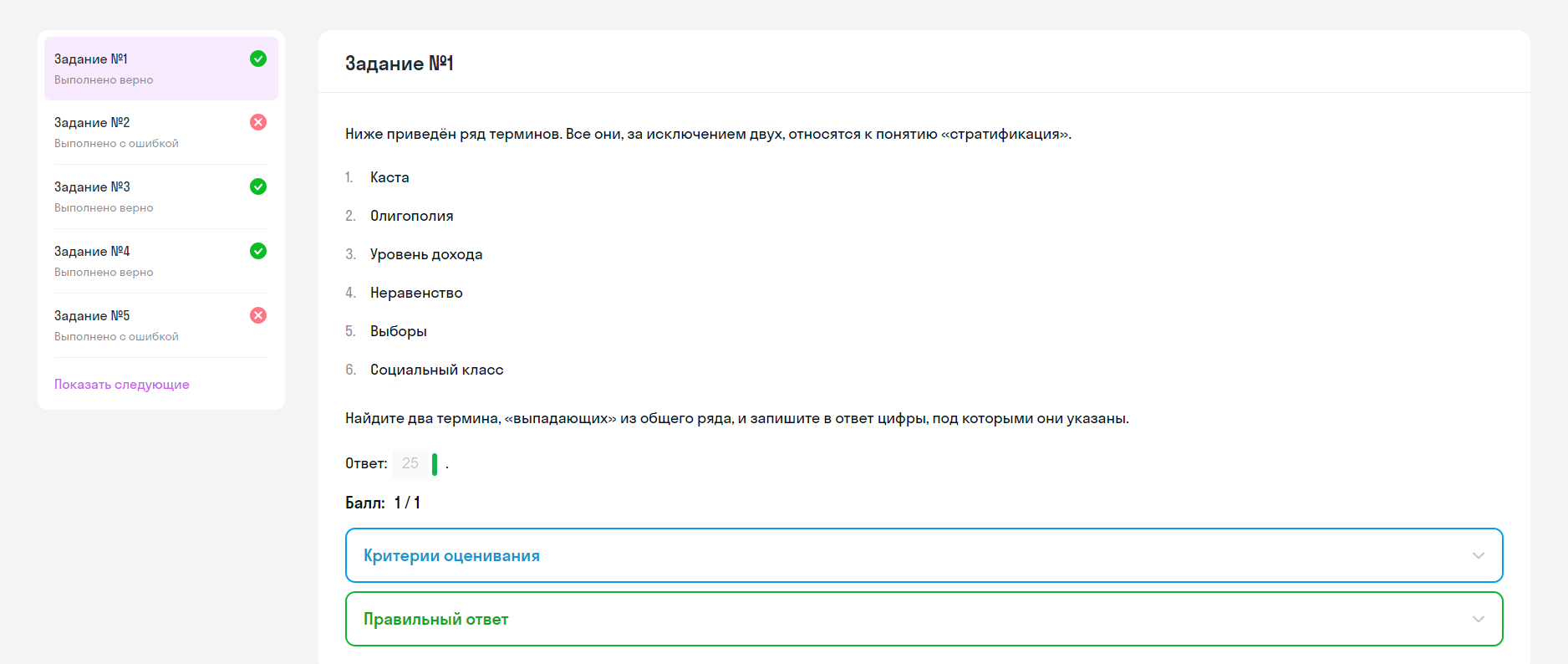
Две окружности касаются внешним образом в точке С. Прямая касается меньшей окружности в точке A, а большей — в точке B, отличной от A. Прямая AС вторично пересекает большую окружность в точке D, прямая BС вторично пересекает меньшую окружность в точке E.

а) Докажите, что прямая AE параллельна прямой BD.

б) Пусть L — отличная от D точка пересечения отрезка DE с большей окружностью. Найдите EL, если радиусы окружностей равны 2 и 3.

а) Пусть общая касательная к данным окружностям, проведённая через точку C, пересекает общую касательную AB в точке M. Тогда MA = МС = МВ, то есть медиана СМ треугольника АВС равна половине стороны АВ. Значит, \angle ACB = 90°. Тогда \angle АСЕ = 90°, поэтому АЕ — диаметр меньшей окружности. Следовательно, прямая АЕ перпендикулярна прямой АВ. Аналогично докажем, что прямая BD перпендикулярна прямой АВ. Прямые АЕ и BD перпендикулярны одной и той же прямой АВ, значит, они параллельны.

б) Пусть радиусы окружностей равны r и R, где r\lt R. Опустим перпендикуляр ОН из центра О меньшей окружности на диаметр BD большей. Тогда

ОН^2 = (R + r)^2-(R-r)^2 = 4rR.

Опустим перпендикуляр EF из точки Е на BD. Тогда

DE = \sqrt{EF^2 + DF^2} = \sqrt{OH^2 +(BD-BF)^2} =

= \sqrt{4rR + (2R-2r)^2} = 2\sqrt{R^2+r^2-Rr} = 2\sqrt{9 + 4-6} = 2\sqrt7 .

Отрезок АС —высота прямоугольного треугольника АВЕ, проведённая из вершины прямого угла, а ЕВ и ED — секущие к большей окружности, проведённые из одной точки, поэтому

EL\cdot DE = EC\cdot EB = AE^2.

Следовательно,

EL = \dfrac{EC\cdot EB}{ED}=\dfrac{AE^2}{ED}= \dfrac{16}{2\sqrt7} =\dfrac{8\sqrt7}{7}.

Ответ: \dfrac{8\sqrt7}{7}.

2 балл	Если обоснованно получены верные ответы в обоих пунктах
1 балл	Если обоснованно получен верный ответ в пункте а или получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов
0 баллов	Если решение не соответствует ни одному из критериев, перечисленных выше

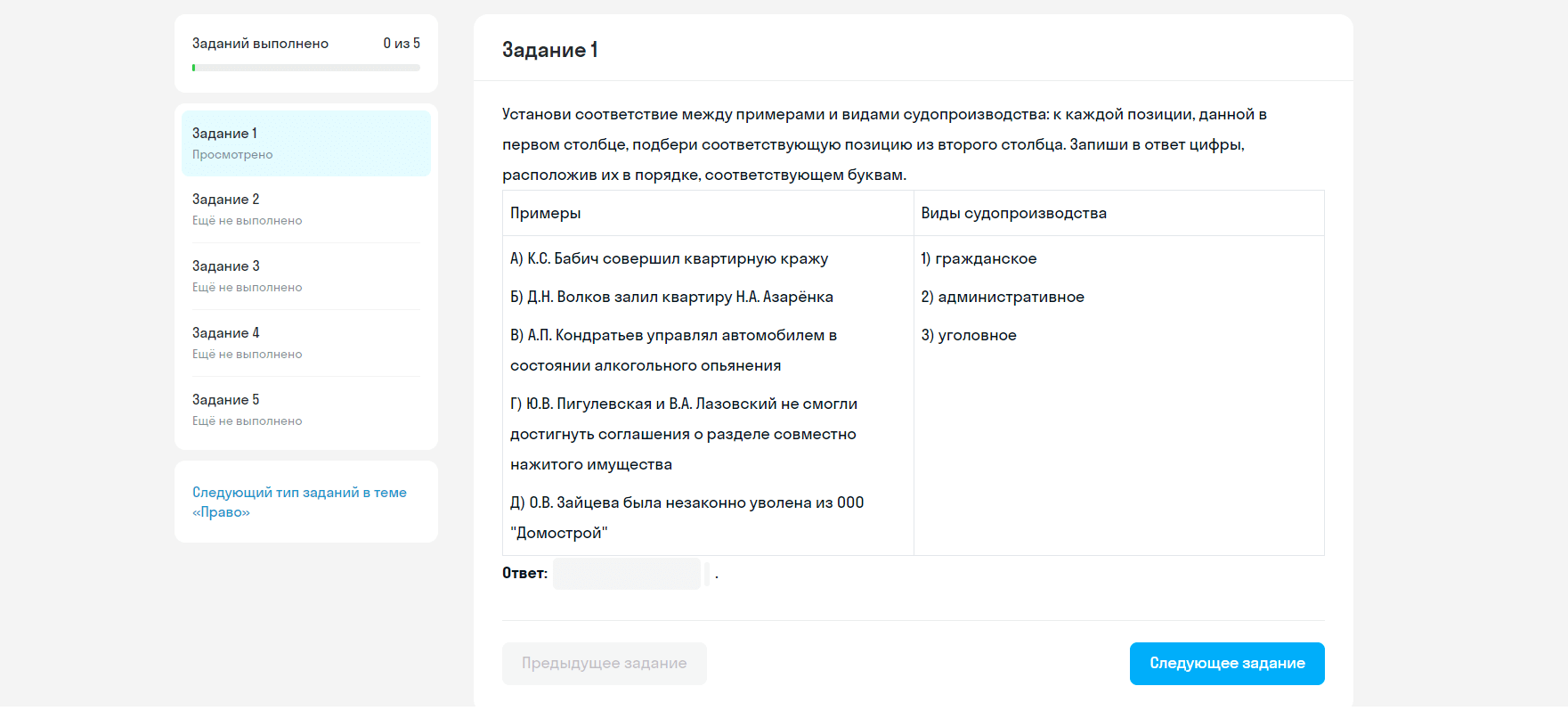
Окружность с центром O вписана в угол, равный 60^\circ. Окружность большего радиуса с центом O_1 также вписана в этот угол и проходит через точку O.

а) Докажите, что радиус второй окружности вдвое больше радиуса первой.

б) Найдите длину общей хорды этих окружностей, если известно, что радиус первой окружности равен 2\sqrt3.

Решение.

а) Очевидно, центры обеих окружностей лежат на биссектрисе угла. Обозначим вершину угла за C, точки касания первой окружности со сторонами угла за A и B, второй — за A_1 и B_1, радиусы окружностей за r и R. Тогда \angle OCA-30\degree, поэтому CO=2AO. Аналогично CO_1=2O_1 A_1, откуда 2R=2O_1 A_1=CO_1=CO+OO_1=2r+R, т.е. R=2r, что и требовалось.

б)Обозначим точку пересечения окружностей за T. Тогда общая хорда — удвоенная высота треугольника TOO_1, проведённая из вершины T. Вычислим её 2h_T = \dfrac{4S_{OO_1T}}{OO_1}=\dfrac{2OT\cdot \sqrt{OO_1^2-0.25OT^2}}{OO_1} = \dfrac{r\cdot \sqrt{4R^2-r^2}}{R} = \dfrac{r^2 \cdot \sqrt{15}}{2r}= \dfrac{2\sqrt{3} \cdot \sqrt{15}}{2}=3 \sqrt{5}

Ответ: 3 \sqrt{5}.

2 балл	Если обоснованно получены верные ответы в обоих пунктах
1 балл	Если обоснованно получен верный ответ в пункте а или получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов
0 баллов	Если решение не соответствует ни одному из критериев, перечисленных выше

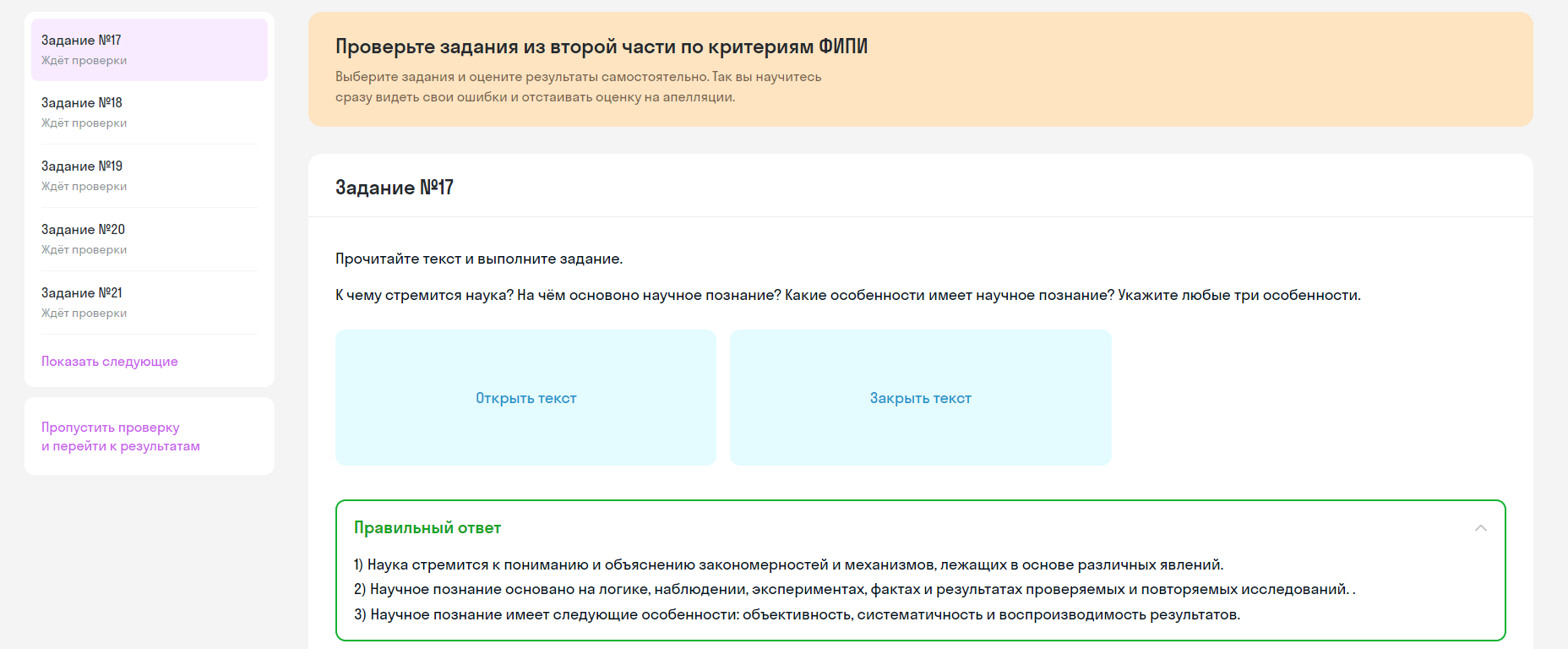
Две окружности с центрами O_1 и O_2 пересекаются в точках A и B, причём точки O_1 и O_2 лежат по разные стороны от прямой AB. Продолжения диаметра CA первой окружности и хорды CB этой окружности пересекают вторую окружности в точках D и E соответственно.

а) Докажите, что треугольники CBD и O_1AO_2 подобны.

б) Найдите AD, если \angle DAE = \angle BAC, радиус второй окружности втрое больше радиуса первой и AB = 3.

Решение.

а) Заметим, что AB\perp O_1O_2, так как линия центров O_1O_2 содержит биссектрисы равнобедренных треугольников АО_1В и АО_2В.

Тогда \angle AO_1O_2 = \dfrac{\angle AO_1B}{2}= \angle АСВ и \angle AO_2O_1 = \dfrac{\angle AO_2B}{2}= \angle АDВ. Значит, \triangle CBD \backsim \triangle O_1AO_2 по двум углам.

б) Из равенства углов \angle AO_1O_2 = \angle ACB, следует параллельность прямых: CB\parallel O_1O_2. Поэтому, учитывая, что AB\perp O_1O_2, получаем: AB\perp CE. Значит, \angle ABE = 90°, а АЕ — диаметр окружности.

Равнобедренные треугольники АО_1В и AO_2D подобны, поскольку

\angle O_1BA = \angle O_1AB = \angle BAC = \angle DAE = \angle O_2AD = \angle O_2DA.

Значит, \dfrac{AD}{AB} = \dfrac{AO_2}{AO_1}, откуда AD = \dfrac{AO_2}{AO_1} \cdot АВ = 9.

Ответ: 9.

2 балл	Если обоснованно получены верные ответы в обоих пунктах
1 балл	Если обоснованно получен верный ответ в пункте а или получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов
0 баллов	Если решение не соответствует ни одному из критериев, перечисленных выше

Как пользоваться тренажёром

Инструкция

Сперва выберите предмет: обществознание, русский язык, базовую или профильную математику. Далее — формат. Это могут быть задания по конкретной теме или полноценный пробный экзамен со всеми типами заданий и темами по кодификатору.

Первое поможет тогда, когда надо отточить задания лишь по нескольким разделам программы. Выполнять весь тест для этого не нужно. Вместо этого можно выбрать раздел и темы внутри него, чтобы отработать все типы заданий, которые могут попасться на экзамене.

Переключаться между ними можно через кнопку Следующий тип заданий в теме.

Если же остановиться на пробном экзамене, можно будет выбрать один из нескольких вариантов. Далее тренажёр ознакомит вас со всеми условиями пробника: сколько будет заданий и какого типа, что понадобится для выполнения.

Обратите внимание: пробный экзамен в тренажёре повторяет условия реального. А значит, это работа на время, которое будет отсчитывать таймер. Если нужно, во время работы можно будет поставить таймер на паузу. Пока она активна, все задания на экране будут скрыты.

В начале пробника всегда будет инструкция. Она напомнит, какие бывают типы заданий в ЕГЭ, чем они отличаются. А также научит добавлять ответы в тренажёр, чтобы тот правильно их обработал.

Слева — все задания пробника по порядку. Их можно переключать здесь же или нажатием кнопки Следующее задание. Как и на реальном экзамене, задания можно выполнять по очереди или в произвольном порядке. С последним помогут кнопки Показать следующие и Показать предыдущие.

Если задание даётся трудно, перейдите к следующему. Позже можно будет вернуться к пропущенным, если останется время. По окончании теста можно не дожидаться, пока сработает таймер, и нажать Завершить тест. Тогда тренажёр перейдёт к проверке результатов.

Разбор результатов начинается со 2 части пробника. Здесь вы сможете сами сравнить ответ с верным и выставить количество баллов. Это несложно — на той же странице мы понятным языком изложили все критерии оценивания.

После этого тренажёр покажет, сколько баллов вы набрали за экзамен. Здесь же будет видно, в какой части и номерах были ошибки. Разобрать их точнее можно с помощью кнопки под результатами.

В разделе с разбором ошибок можно сверить свои ответы из 1 части экзамена с правильными. Это поможет закрепить знания по теме и не ошибиться в следующий раз.

Удачи и высоких баллов!

Окружности и системы окружностей: задания и теория

Как пользоваться тренажёром

Инструкция