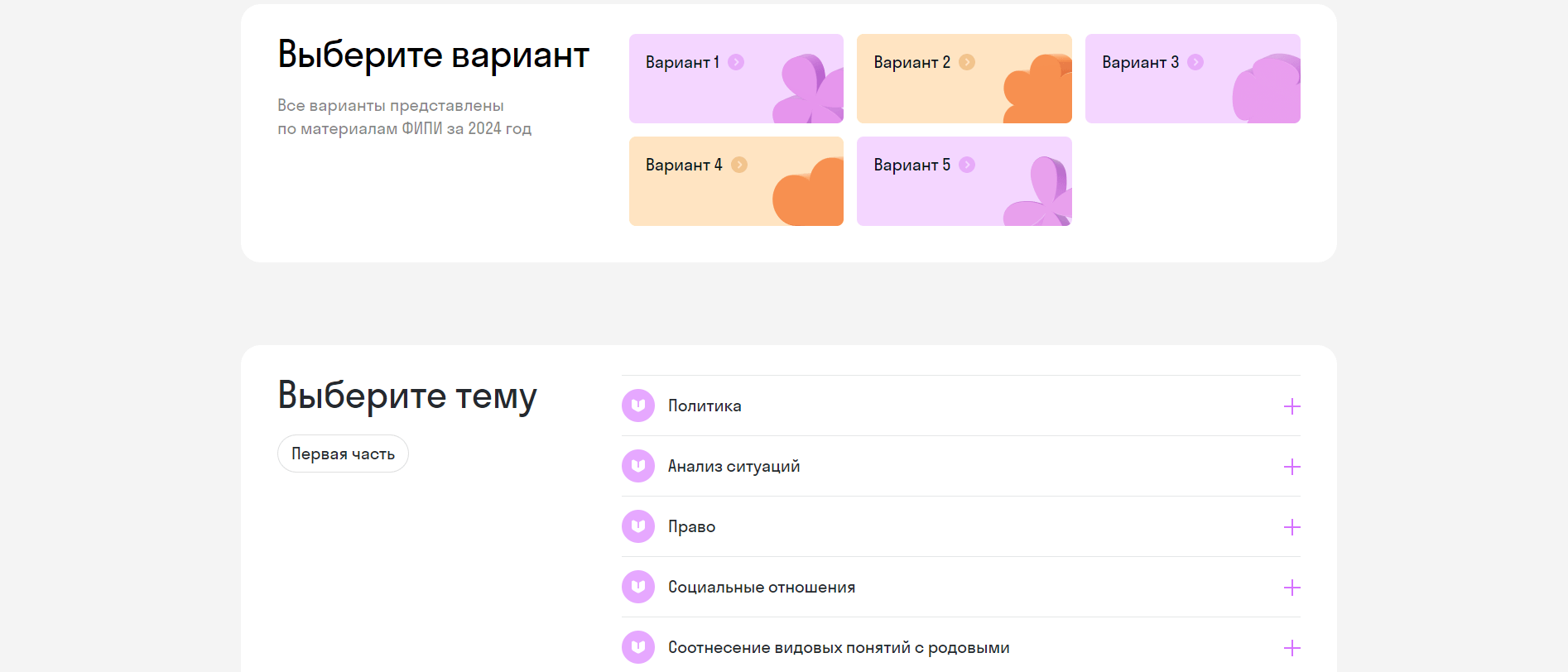
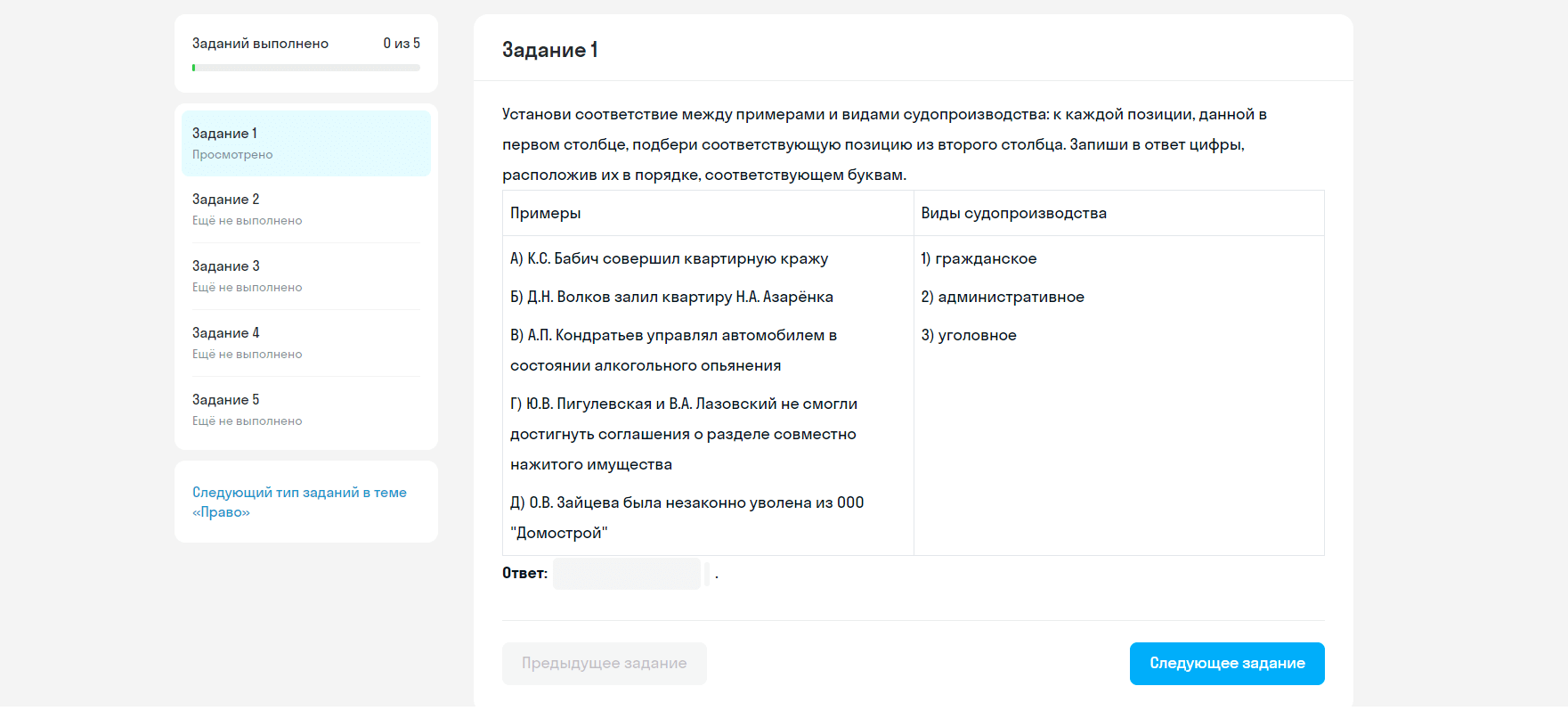
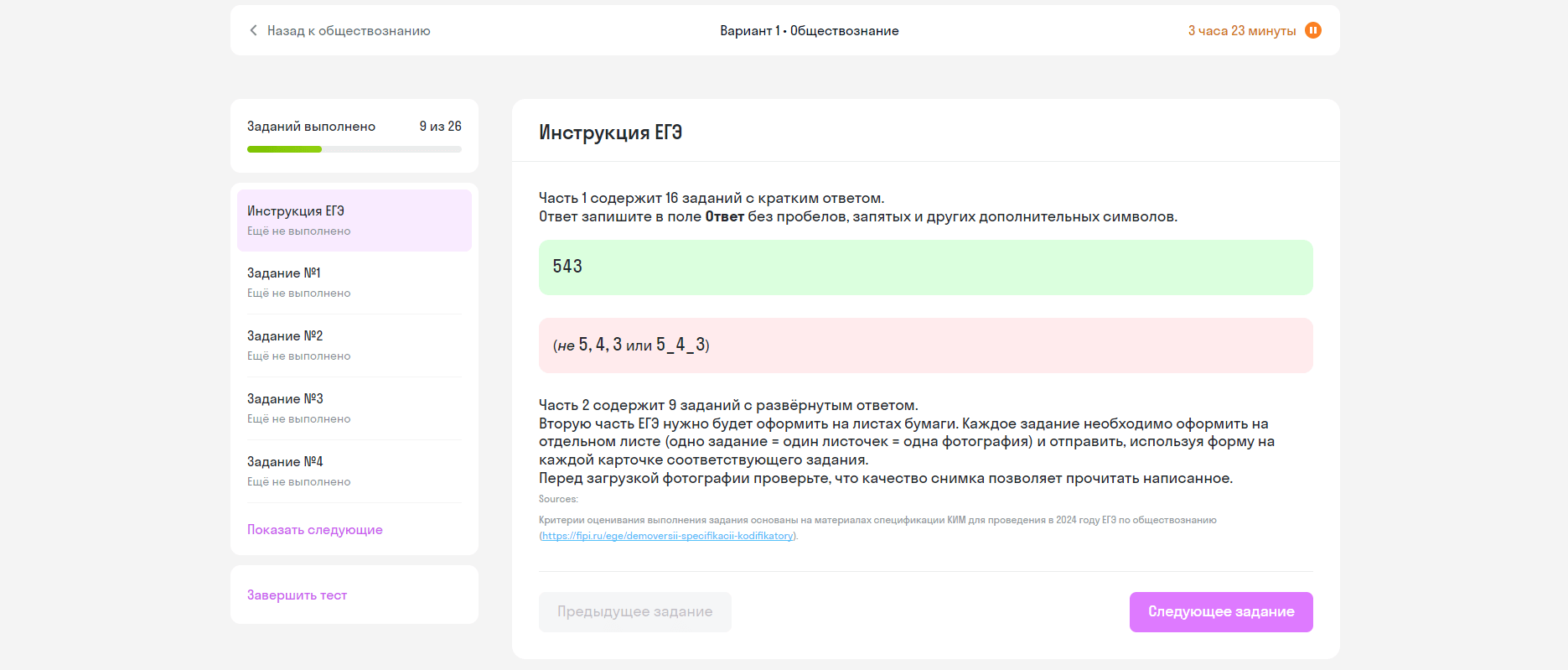
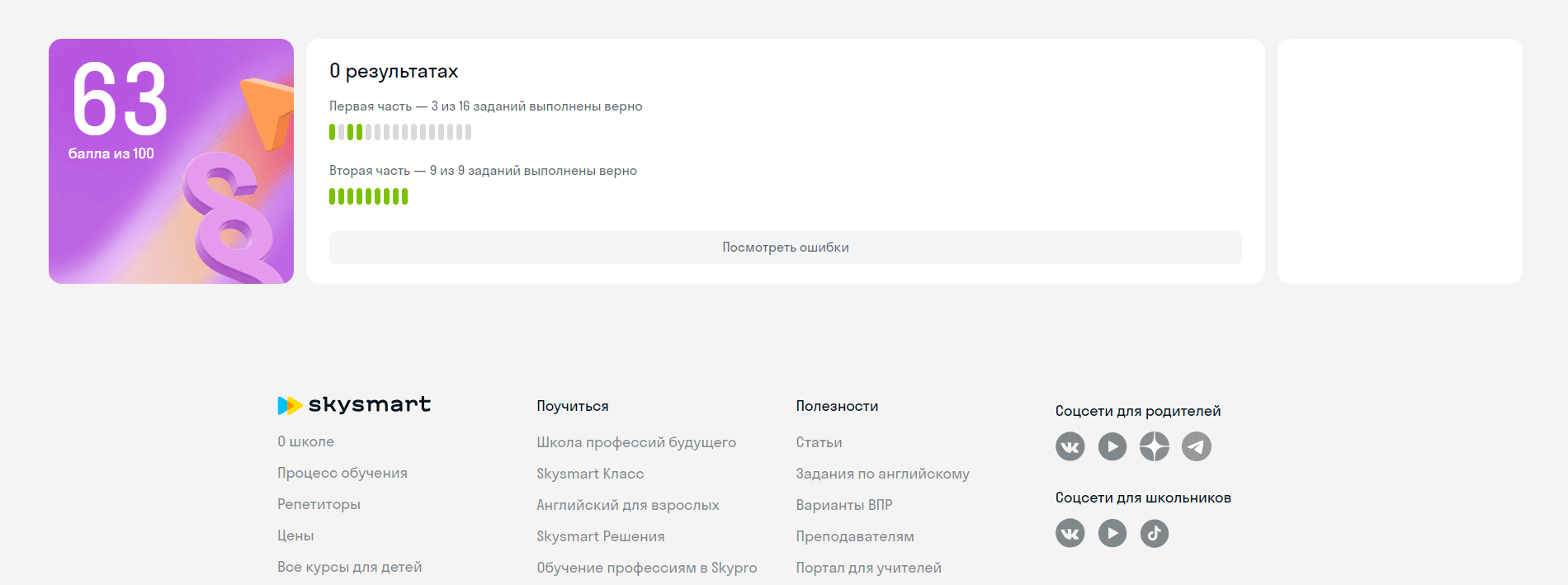
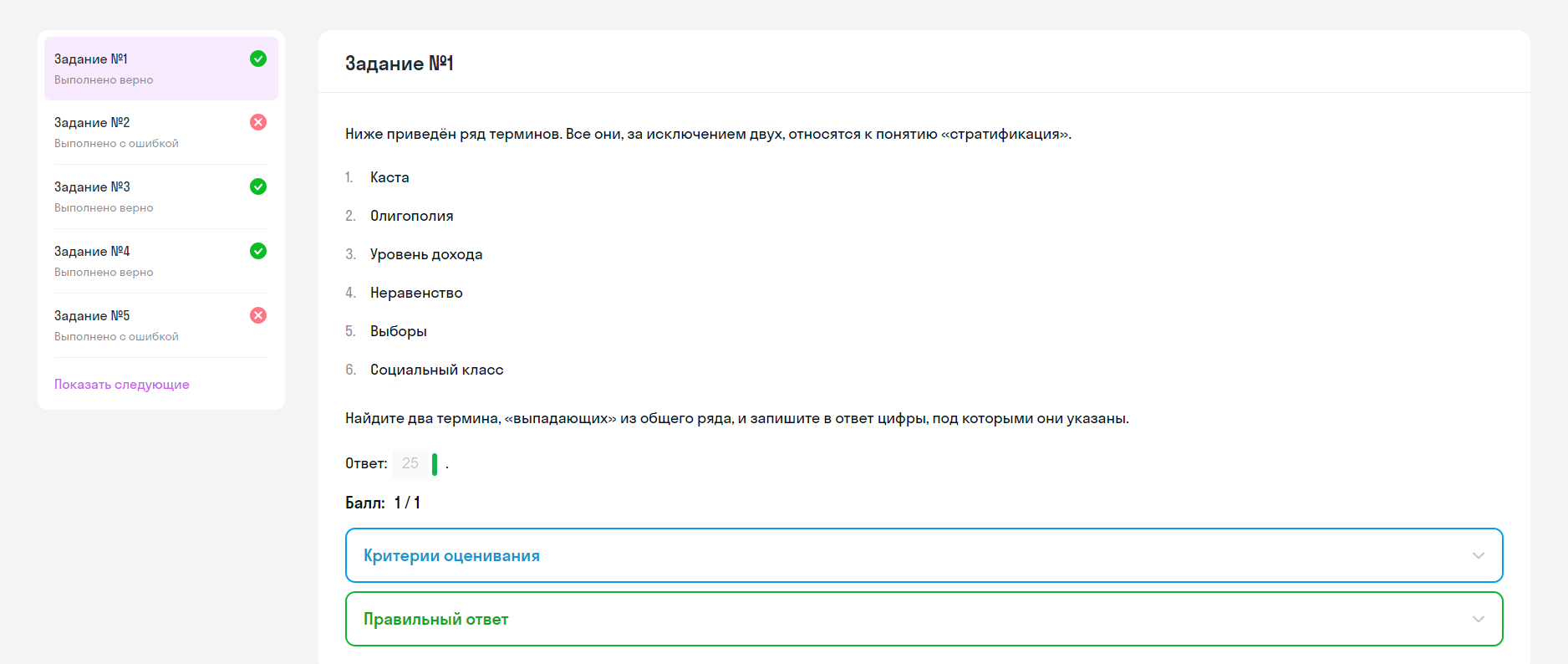
Изучайте английский в любое время, в любом месте

Задание с развернутым ответом

Выполните его и проверьте ответ по критериям ФИПИ

а) 4\cos^3\left(x-\dfrac{\pi}2\right)- 3\cos \left(x-\dfrac{\pi}{2}\right)=0

б) Найди все корни уравнения, удовлетворяющие промежутку [2\pi;3\pi]. Ответ запишите через точку с запятой.

а) Воспользуемся формулами приведения:

\sin^3 x - 3\sin x =0

\sin x (4\sin^2 x -3)=0

Разложим на множители:

\sin x \left( \sin x - \dfrac{\sqrt{3}}{2} \right) \left( \sin x + \dfrac{\sqrt{3}}{2} \right)=0

\sin x=0, x=\pi n, \space n \in \Z;

\sin x=\dfrac{\sqrt{3}}{2}

x=\dfrac{\pi}{3} + 2\pi k_1, \space k_1 \in \Z,

x=\dfrac{2\pi}{3} + 2\pi k_2, \space k_2 \in \Z;

\sin x=-\dfrac{\sqrt{3}}{2}

x=-\dfrac{\pi}{3} + 2\pi m_1, \space m_1 \in \Z,

x=-\dfrac{2\pi}{3} + 2\pi m_2, \space m_2 \in \Z;

Объединим полученные серии:

x=\pi n, \space n \in \Z

x = \dfrac{\pi}{3} + \pi k, \space k \in \Z

x = \dfrac{2\pi}{3} + \pi m, \space m \in \Z

б) 2\pi;\dfrac{7\pi}{3};\dfrac{8\pi}{3};3\pi

2 балл	Если обоснованно получены верные ответы в обоих пунктах
1 балл	Если обоснованно получен верный ответ в пункте а или получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов
0 баллов	Если решение не соответствует ни одному из критериев, перечисленных выше

а) 3\sin 4x +2\sin 2x +6 \cos 2x +2=0

б) Найди все корни уравнения, принадлежащие промежутку \left[\dfrac{\pi}{2};\dfrac{3\pi}{2}\right].

а) 6\sin 2x \cos 2x +2\sin 2x +6\cos 2x +2=0

3\sin 2x \cos 2x + \sin 2x +3 \cos 2x +1=0

3\cos 2x (\sin 2x +1) +(\sin 2x +1)=0

(\sin 2x +1)(3\cos 2x+1)=0

\sin 2x=-1

2x=\dfrac{3\pi}{2} +2\pi n, \space n \in \Z

x=\dfrac{3\pi}{4} + \pi n, \space n \in \Z

3\cos 2x+1=0

\left[ \begin{aligned} 2x=\pi - \arccos \left( \dfrac{1}{3} \right) +2\pi k, \space k \in \Z\\ 2x=\pi + \arccos \left( \dfrac{1}{3} \right) +2\pi m, \space m \in \Z \end{aligned} \right.

\left[ \begin{aligned} x=\dfrac{\pi}{2} - \dfrac{1}{2} \arccos \left( \dfrac{1}{3} \right) +\pi k, \space k \in \Z\\ x=\dfrac{\pi}{2} + \dfrac{1}{2} \arccos \left( \dfrac{1}{3} \right) +\pi m, \space m \in \Z \end{aligned} \right.

б) \dfrac{\pi}{2}+\dfrac{1}{2}\arccos \left( \dfrac{1}{3} \right); \dfrac{3\pi}{4};\dfrac{3\pi}{2}-\dfrac{1}{2}\arccos \left( \dfrac{1}{3} \right)

2 балл	Если обоснованно получены верные ответы в обоих пунктах
1 балл	Если обоснованно получен верный ответ в пункте а или получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов
0 баллов	Если решение не соответствует ни одному из критериев, перечисленных выше

Найди все корни уравнения 2\cos\left(x-\dfrac{15\pi}2\right)\cdot\cos x=\sin x, удовлетворяющие промежутку (2\pi;3\pi) в порядке возрастания через точку с запятой.

Воспользуемся периодичностью косинуса:

\cos\left(x - \frac{15\pi}2\right)=\cos\left(x-\frac{3\pi}{2}\right)

Воспользуемся четностью косинуса:

\cos\left(x-\frac{3\pi}{2}\right)=\cos\left(\frac{3\pi}{2} -x\right)

Воспользуемся формулами приведения:

\cos\left(\frac{3\pi}{2} -x\right)=-\sin\left( x\right)

-2\sin x \cos x = \sin x

Разложим на множители

\sin x=0, \cos=-\frac{1}{2}

\pi n,\space n\in\mathbb{Z}

\pm \dfrac{2\pi}3+2\pi m,\space m\in\mathbb{Z}

\dfrac{8\pi}{3}

2 балл	Если обоснованно получены верные ответы в обоих пунктах
1 балл	Если обоснованно получен верный ответ в пункте а или получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов
0 баллов	Если решение не соответствует ни одному из критериев, перечисленных выше

Найди все корни уравнения\cos (2 (\pi+x)) + \sqrt{3} \cos \left(\dfrac{7\pi}{2} - x \right) = \cos \left( \dfrac{7\pi}{2} \right) +1 , удовлетворяющие промежутку \left[\dfrac{5\pi}{7};\dfrac{11\pi}{5}\right].

Расположи корни в порядке возрастания через точку с запятой.

\cos (2\pi +2x)-\sqrt{3} \sin x -\cos\left(\dfrac{7\pi}{2}\right) -1=0

\cos 2x -\sqrt{3} \sin x -1=0

1-2\sin^2 x - \sqrt{3} \sin x -1 =0

2\sin^2 x +\sqrt{3} \sin x =0

\sin x (2\sin x +\sqrt{3})=0

\sin x =0

x = \pi n , \space n \in \Z

\sin x = -\dfrac{\sqrt{3}}{2}

x = -\dfrac{\pi}{3} +2\pi k, \space k \in \Z

x = -\dfrac{2\pi}{3} +2\pi m, \space m \in \Z

\pi;\dfrac{4\pi}{3};\dfrac{5\pi}{3};2\pi

2 балл	Если обоснованно получены верные ответы в обоих пунктах
1 балл	Если обоснованно получен верный ответ в пункте а или получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов
0 баллов	Если решение не соответствует ни одному из критериев, перечисленных выше

Как пользоваться тренажёром

Инструкция

Сперва выберите предмет: обществознание, русский язык, базовую или профильную математику. Далее — формат. Это могут быть задания по конкретной теме или полноценный пробный экзамен со всеми типами заданий и темами по кодификатору.

Первое поможет тогда, когда надо отточить задания лишь по нескольким разделам программы. Выполнять весь тест для этого не нужно. Вместо этого можно выбрать раздел и темы внутри него, чтобы отработать все типы заданий, которые могут попасться на экзамене.

Переключаться между ними можно через кнопку Следующий тип заданий в теме.

Если же остановиться на пробном экзамене, можно будет выбрать один из нескольких вариантов. Далее тренажёр ознакомит вас со всеми условиями пробника: сколько будет заданий и какого типа, что понадобится для выполнения.

Обратите внимание: пробный экзамен в тренажёре повторяет условия реального. А значит, это работа на время, которое будет отсчитывать таймер. Если нужно, во время работы можно будет поставить таймер на паузу. Пока она активна, все задания на экране будут скрыты.

В начале пробника всегда будет инструкция. Она напомнит, какие бывают типы заданий в ЕГЭ, чем они отличаются. А также научит добавлять ответы в тренажёр, чтобы тот правильно их обработал.

Слева — все задания пробника по порядку. Их можно переключать здесь же или нажатием кнопки Следующее задание. Как и на реальном экзамене, задания можно выполнять по очереди или в произвольном порядке. С последним помогут кнопки Показать следующие и Показать предыдущие.

Если задание даётся трудно, перейдите к следующему. Позже можно будет вернуться к пропущенным, если останется время. По окончании теста можно не дожидаться, пока сработает таймер, и нажать Завершить тест. Тогда тренажёр перейдёт к проверке результатов.

Разбор результатов начинается со 2 части пробника. Здесь вы сможете сами сравнить ответ с верным и выставить количество баллов. Это несложно — на той же странице мы понятным языком изложили все критерии оценивания.

После этого тренажёр покажет, сколько баллов вы набрали за экзамен. Здесь же будет видно, в какой части и номерах были ошибки. Разобрать их точнее можно с помощью кнопки под результатами.

В разделе с разбором ошибок можно сверить свои ответы из 1 части экзамена с правильными. Это поможет закрепить знания по теме и не ошибиться в следующий раз.

Удачи и высоких баллов!

Тригонометрические уравнения, разложение на множители: задания и теория

Как пользоваться тренажёром

Инструкция