Изучайте английский в любое время, в любом месте

Задание с развернутым ответом

Выполните его и проверьте ответ по критериям ФИПИ

Найдите все значения a, при каждом из которых множество решений неравенства

\dfrac{a-(a^2-2a-3)\sin x+4}{1,5+0,5\cos 2x+a^2}\lt1

содержит отрезок \left[-2\pi ;-\dfrac{7\pi}6\right].

Решение.

Заметим, что при любых значениях переменной х и параметра a знаменатель дроби в левой части неравенства положителен, поэтому исходное неравенство равносильно неравенству

a - (a^2 - 2а - 3)\sin x + 4 \lt 0,5(1 - 2\sin^2x) + a^2 + 1,5.

Для того, чтобы множество решений неравенства содержало отрезок \left[ -2π; -\dfrac{7\pi}{6} \right] синус должен принимать все значения 0 ≤ \sin x ≤ 1 (см. рисунок)

Пусть \sin x = t, тогда неравенство принимает вид

а - (а^2 - 2а -3)t + 4 \lt 0,5(1 - 2t^2) +а^2 + 1,5 \Leftrightarrow

t^2- (a^2-2a-3)t-a^2+a + 2 \lt 0

Рассмотрим функцию f(t) = t^2 - (а^2-2а - 3)t - a^2+a + 2 Для того, чтобы множество решений последнего неравенства содержало отрезок [0; 1] необходимо и достаточно, чтобы одновременно выполнялись два условия f(0) \lt 0 и f(1) \lt 0

\begin{cases} f(0) \lt 0, \\ f(1) \lt 0 \end{cases} \Leftrightarrow

\begin{cases} -a^2 + a+2\lt 0 \\ -2a^2 + 3a + 6\lt 0 \end{cases} \Leftrightarrow

\begin{cases} \left[\begin{array}{l} a \lt -1, \\ a \gt 2, \end{array}\right. \\ \left[\begin{array}{l} a \lt \dfrac{3-\sqrt{57}}{4}, \\ a \gt \dfrac{3+\sqrt{57}}{4} \end{array}\right. \end{cases} \Leftrightarrow

\left[\begin{array}{l} a \lt \dfrac{3-\sqrt{57}}{4}, \\ a \gt \dfrac{3+\sqrt{57}}{4}. \end{array}\right.

Ответ: a \lt \dfrac{3-\sqrt{57}}{4}; a \gt \dfrac{3+\sqrt{57}}{4}.

Найдите все значения a, при каждом из которых наименьшее значение функции

f(x) = x - 2|x| + \left|x^2 - 2(a+1)x + a^2 + 2a\right|

больше -4.

\left|x^2 - 2(a+1)x + a^2 + 2a\right|=2|x|-x-4

Пусть g(x)=\left|x^2 - 2(a+1)x + a^2 + 2a\right|;\ h(x)=2|x|-x-4.
График h(x) не зависит от параметра.
График g(x) — парабола, отраженная относительно оси Ox.
Вершина: (a+1;\ 1), нули функции: x=a;\ x=a+2. Функция «скользит» вдоль оси Ox.
Графики не имеют общих точек, если g(x) целиком оказывается внутри уголка h(x).
На рисунке показаны два крайних значения функции.
При a=2 общая точка (4;\ 0).
При a=-\dfrac54 касание ветви параболы и прямой y=-3x-4.

Ответ: (-1,25;\ 2).

Найдите все значения a, при каждом из которых множество значений функции

y=\dfrac{5a+150x-10ax}{100x^2+20ax+a^2+25}

содержит отрезок [0;1].

Запишем функцию в виде у =\dfrac{5a +10(15 -a)x }{(10x +a)^2 + 25}. Если при некоторых значениях a существуют такие числа x_0, x_1, что выполняются равенства 0= \dfrac{5a + 10(15-a)x_0}{(10x_0+a)^2 + 25} и 1 = \dfrac{5a + 10(15-a)x_1}{(10x_1+a)^2+ 25}, то отрезок [0; 1] будет принадлежать множеству значений данной функции.

Первое уравнение: 0 = \dfrac{5a + 10(15-a)x}{(10x_0+a)^2 + 25}; 10(a-15)x= 5a уравнение имеет решение при любом a ≠ 15.

Второе уравнение: 1=\dfrac{5a + 10(15-a)x}{(10x+a)^2 + 25}; 100х^2 +30(а-5)х + a^2 +5a + 25 = 0.

Уравнение имеет решения тогда и только тогда, когда его дискриминант неотрицателен:

D = 900(a - 5)^2 - 400(a^2 - 5a + 25) ≥ 0; 500(a^2 -14a + 25) ≥ 0;

(a-7 + 2\sqrt6)(a-7-2\sqrt6)≥0.

Решением этого неравенства является множество (-\infty; 7-2\sqrt6], [7 + 2\sqrt6; +∞). Следовательно, условию задачи удовлетворяют все значения a, принадлежащие множеству (-\infty; 7- 2\sqrt6], [7 + 2\sqrt6; 15), (15; +\infty).

Ответ: (-\infty; 7-2\sqrt6] , [7 + 2\sqrt6; 15), (15; +\infty).

Как пользоваться тренажёром

Инструкция

Сперва выберите предмет: обществознание, русский язык, базовую или профильную математику. Далее — формат. Это могут быть задания по конкретной теме или полноценный пробный экзамен со всеми типами заданий и темами по кодификатору.

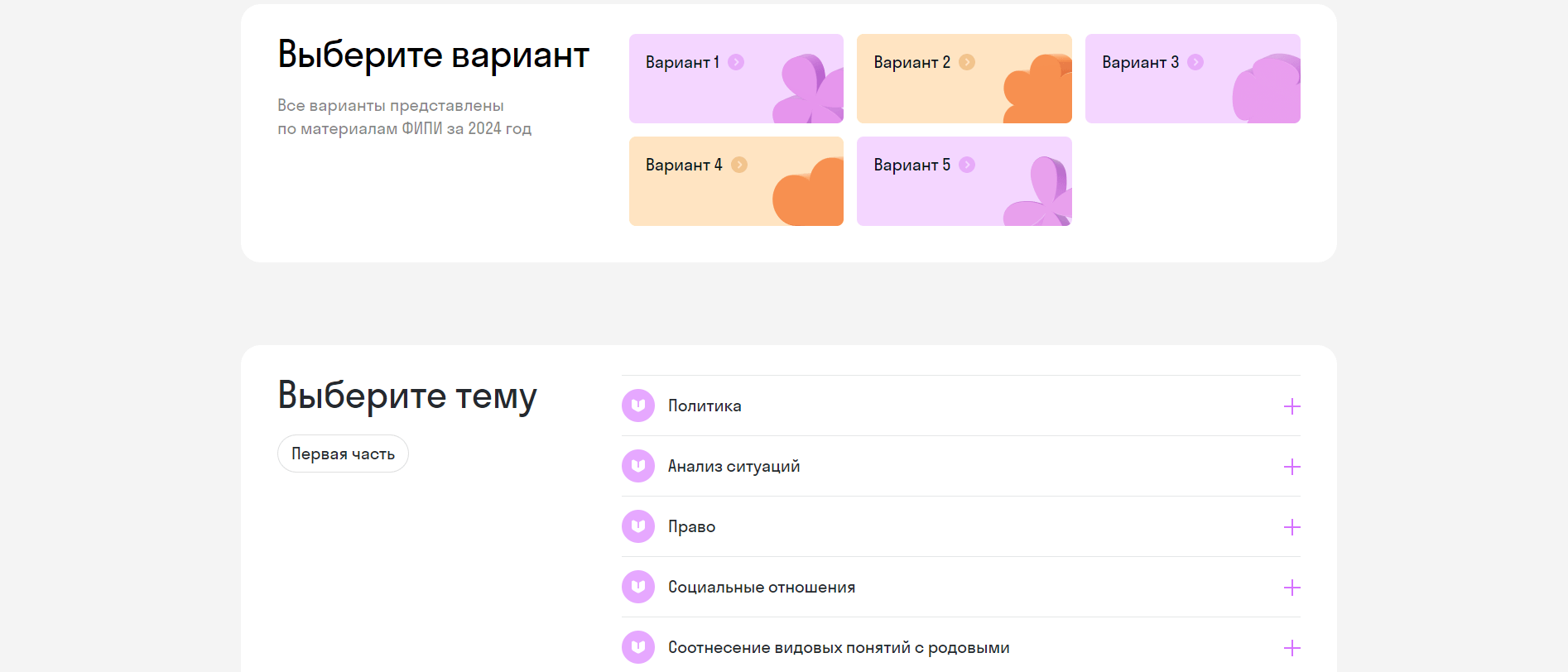
Первое поможет тогда, когда надо отточить задания лишь по нескольким разделам программы. Выполнять весь тест для этого не нужно. Вместо этого можно выбрать раздел и темы внутри него, чтобы отработать все типы заданий, которые могут попасться на экзамене.

Переключаться между ними можно через кнопку Следующий тип заданий в теме.

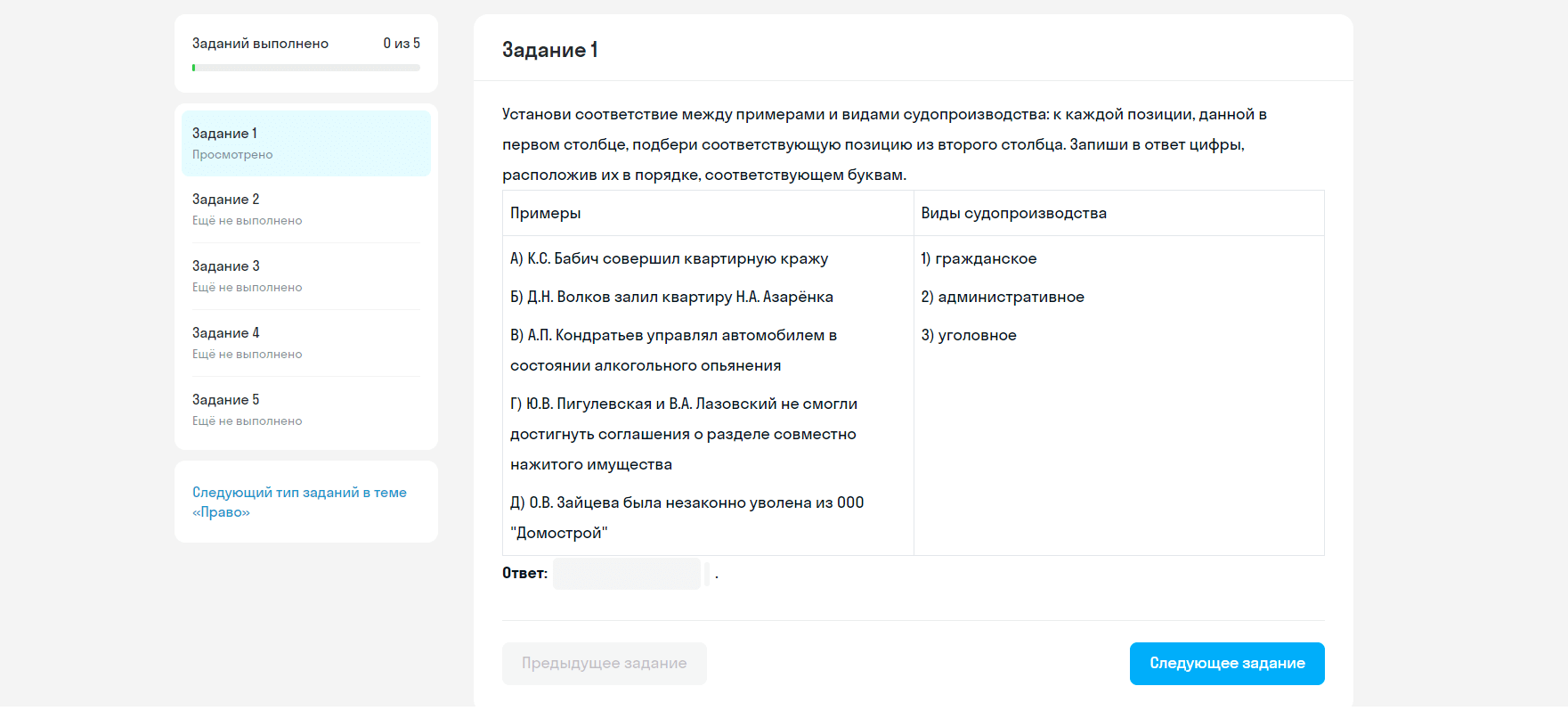
Если же остановиться на пробном экзамене, можно будет выбрать один из нескольких вариантов. Далее тренажёр ознакомит вас со всеми условиями пробника: сколько будет заданий и какого типа, что понадобится для выполнения.

Обратите внимание: пробный экзамен в тренажёре повторяет условия реального. А значит, это работа на время, которое будет отсчитывать таймер. Если нужно, во время работы можно будет поставить таймер на паузу. Пока она активна, все задания на экране будут скрыты.

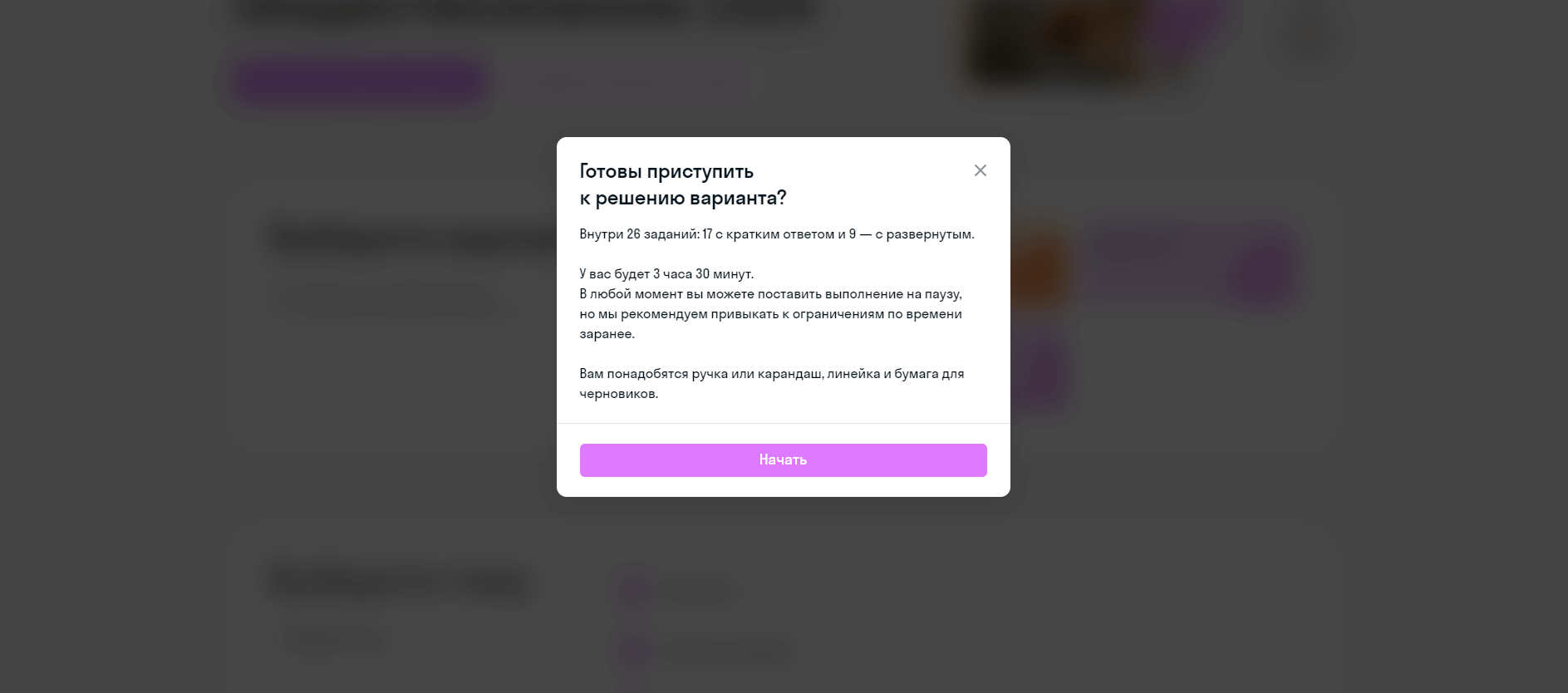
В начале пробника всегда будет инструкция. Она напомнит, какие бывают типы заданий в ЕГЭ, чем они отличаются. А также научит добавлять ответы в тренажёр, чтобы тот правильно их обработал.

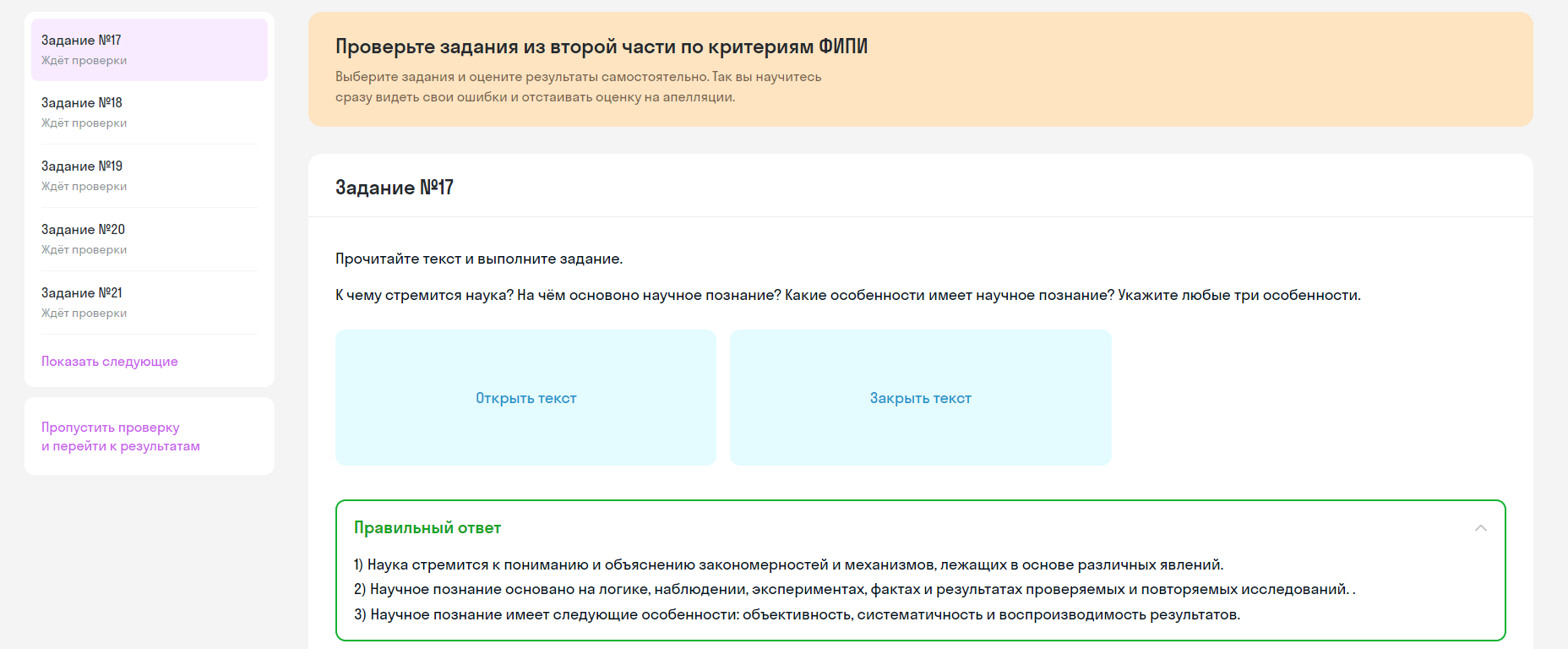
Слева — все задания пробника по порядку. Их можно переключать здесь же или нажатием кнопки Следующее задание. Как и на реальном экзамене, задания можно выполнять по очереди или в произвольном порядке. С последним помогут кнопки Показать следующие и Показать предыдущие.

Если задание даётся трудно, перейдите к следующему. Позже можно будет вернуться к пропущенным, если останется время. По окончании теста можно не дожидаться, пока сработает таймер, и нажать Завершить тест. Тогда тренажёр перейдёт к проверке результатов.

Разбор результатов начинается со 2 части пробника. Здесь вы сможете сами сравнить ответ с верным и выставить количество баллов. Это несложно — на той же странице мы понятным языком изложили все критерии оценивания.

После этого тренажёр покажет, сколько баллов вы набрали за экзамен. Здесь же будет видно, в какой части и номерах были ошибки. Разобрать их точнее можно с помощью кнопки под результатами.

В разделе с разбором ошибок можно сверить свои ответы из 1 части экзамена с правильными. Это поможет закрепить знания по теме и не ошибиться в следующий раз.

Удачи и высоких баллов!

Функции, зависящие от параметра: задания и теория

Как пользоваться тренажёром

Инструкция